miccai 2024 centerline boundary dice loss for vascular segmentation
miccai 2024centerline boundary dice loss for vascular segmentation
中心线边界dice损失用于血管分割
彭成世1, 捷斯·胡1,2, 颜武洋1,2, 齐乐高1, 韦磊1, 马霆1,2,3,4
- 哈尔滨工业大学(深圳)电子与信息工程学院,深圳,中国
- 彭程实验室,深圳,中国
- 哈尔滨工业大学(深圳)通信与网络技术省重点实验室,深圳,中国
- 哈尔滨工业大学(深圳)人工智能研究院,深圳,中国
邮箱:tma@hit.edu.cn
摘要:
在医学成像中,血管分割在形态学和功能评估中起着至关重要的作用。传统方法,如中心线dice (cldice) 损失,确保拓扑保留但在捕获几何细节(特别是平移和变形)方面存在缺陷。结合传统dice损失的cldice可以导致直径不平衡,偏向较大的血管。为了解决这些挑战,我们引入了中心线边界dice (cbdice) 损失函数,该函数保持拓扑完整性和几何统一性,确保跨各种血管尺度的一致分割。cbdice通过包括边界感知方面丰富了cldice,从而提高了几何细节捕获能力。它通过基于掩膜距离的方法实现了与边界差异(b-dou)损失相当的性能,增强了平移灵敏度。关键的是,cbdice从血管骨架中整合信息,使直径变化均匀,并在分支处保持一致影响。此外,我们进行了各类dice变体的理论分析(t-x-dice)。我们验证了cbdice在二维和三维、多尺度分割应用中的有效性。特别是在多分支情况下,使用cbdice的方法在近期的michal 2023分割挑战中取得了卓越表现。我们的代码已公开可用,地址为: https://github.com/pengchengshi1220/cbdice.
关键词: 血管分割, 中心线边界损失, 直径平衡
1. 引言
深度学习的进步显著提升了医学图像分割的能力,尤其是在血管方面,革新了诊断和介入放射学。然而,现有的评估指标常常忽视特定领域的要求,如几何细节的不足【10,15】。血管分割遇到的特定挑战包括:1) 保持拓扑完整性;2) 精确的几何分割(如准确的血液动力学分析);3) 基于解剖学的血管网络标记(如处理静脉窦);4) 跨不同血管直径的一致分割并随着几何变化进行直径调整(见图1)。
在本文中,我们寻求解决一个基本问题:如何在血管分割中实现拓扑和几何一致性?近期在深度学习驱动的血管分割领域的重大进展得益于利用生物学知识【4,13,20,17,11,7,14,2】和几何知识【24,13,23,12,18,14】的网络方法。然而,在医学图像分割中设计损失函数以减轻数据不平衡方面的进展有限【6,28,27】。一个全面的分析框架在这一领域仍然缺乏。我们的研究旨在通过提出中心线边界dice (cbdice)损失函数来弥补这一差距。cbdice独特地结合了从血管骨架中提取的半径信息。这种方法促进了不同直径血管的一致分割,关键地保持了拓扑一致性。我们的贡献如下:(1)我们介绍了统一的clx-dice变体,一个结合拓扑完整性和血管直径一致性的血管分割框架。(2) 从中心线dice (cldice)损失中引入几何考虑因素,等效于边界差异过联合 (b-dou)损失的新方法,使用基于掩膜距离的方法,增强了平移敏感性。(3) 我们提出了cbdice通过整合来自血管骨架的信息,适应血管直径的变化,确保分支的一致影响。(4) 我们进行了一般理论分析,以展示不同clx-dice实现的几何变换响应。 除此之外,我们还验证了cbdice在各种血管分割数据集中的有效性,包括二维和三维,以及二元和多类分割任务。
相关工作:
(i) 拓扑学: 保持连接性,如使用非监督的持续同调【4,13,20】,中心线或骨架化技术【11,17】和欧拉特征方法【7】,至关重要。拓扑不变性确保了在平移和变形情况下的几何细节保持。例如,cldice损失函数【17】强调了在捕获几何精度时保持拓扑完整性,但在捕获几何精度(尤其是平移和变形)方面存在不足。这凸显了需要能够和谐平衡拓扑保真度与精准几何表示的分割方法。
(ii) 几何学: 最近的工作通过如b-dou损失【8】和深度编码网络【24】等方法突出了几何性的重要性。技术如动态形状卷积【13】和特征传递【21】在医学图像分割中得到了应用。基于距离图的方法变得普遍,包括使用带符号距离图的形状感知分割【25】,以及基于距离变换图的cnn集成【9】。最近的技术结合了中心线和距离图,展示了在管状结构分割中同时约束骨架和几何形态的能力【23,18】。然而,它们在损失函数中的综合集成不足,这对于扩大适用性和泛化性至关重要。尽管基于cldice的归一化骨架距离变换(nsdt)损失【14】在几何形态和拓扑保真度方面表现出色,传统的损失函数如dice损失仍然受到直径不平衡的影响。
(iii) 不平衡: 在医学图像分割中,不平衡是一个常见问题,传统的dice损失在较大解剖结构上表现出偏差。为了解决这个问题,最近的研究提出了一系列针对不平衡解决方案,包括边界损失【6】、局部dice损失【28】、联合损失【22】和统一焦点损失【27】。这些方法旨在减轻不平衡分割。然而,它们并未特别解决血管网络中直径不平衡的问题,同时忽视了血管网络的连接性。
2. 方法
预备知识
该方法首先通过模型处理输入
x
∈
r
c
i
i
m
e
s
n
x \in \mathbb{r}^{c_i imes n}
x∈rciimesn ,生成输出
y
∈
r
c
o
i
m
e
s
n
y \in \mathbb{r}^{c_o imes n}
y∈rcoimesn ,其中
c
i
c_i
ci 和
c
o
c_o
co 分别表示输入和输出通道的数量。随后,输出
y
y
y 被转换为二值掩码,记为
v
v
v 。这里,
n
n
n 表示像素或体素的总数,定义为
w
i
m
e
s
h
w imes h
wimesh 对于2d图像,或
w
i
m
e
s
h
i
m
e
s
d
w imes h imes d
wimeshimesd 对于3d体积,其中
w
,
h
,
d
w, h, d
w,h,d 分别表示宽度、高度和深度。掩码
v
v
v 定义为
v
=
{
v
i
;
b
j
∣
i
∈
[
1
,
q
]
,
j
∈
[
1
,
k
]
}
,包括值为
1
的掩码点(
v = \{v_i; b_j | i \in [1,q], j \in [1,k]\} ,包括值为1的掩码点(
v={vi;bj∣i∈[1,q],j∈[1,k]},包括值为1的掩码点(v$)和值为0的背景点(
b
b
b )。相应的骨架
s
s
s 由
v
v
v 导出,组成
s
=
{
s
i
;
b
j
s
∣
i
∈
[
1
,
n
]
,
j
∈
[
1
,
m
]
}
s = \{s_i; b_j^s | i \in [1,n], j \in [1,m]\}
s={si;bjs∣i∈[1,n],j∈[1,m]} ,其中
n
n
n 个骨架点(
s
s
s )值为1,
m
m
m 个背景点(
b
s
b^s
bs )值为0。
v
v
v 和
s
s
s 都属于
r
n
\mathbb{r}^n
rn 。下标 p 和 l 分别表示预测和参考。我们从检查传统的 cldice【17】开始,介绍拓扑保留的方法。
t
p
r
e
c
(
s
p
,
v
l
)
=
∣
s
p
∩
v
l
∣
∣
s
p
∣
,
t
s
e
n
s
(
s
l
,
v
p
)
=
∣
s
l
∩
v
p
∣
∣
s
l
∣
t_{prec}(s_p, v_l) = \frac{|s_p \cap v_l|}{|s_p|}, \quad t_{sens}(s_l, v_p) = \frac{|s_l \cap v_p|}{|s_l|}
tprec(sp,vl)=∣sp∣∣sp∩vl∣,tsens(sl,vp)=∣sl∣∣sl∩vp∣
cldice
(
v
p
,
v
l
)
=
2
×
t
p
r
e
c
(
s
p
,
v
l
)
×
t
s
e
n
s
(
s
l
,
v
p
)
t
p
r
e
c
(
s
p
,
v
l
)
+
t
s
e
n
s
(
s
l
,
v
p
)
\text{cldice}(v_p, v_l) = \frac{2 \times t_{prec}(s_p, v_l) \times t_{sens}(s_l, v_p)}{t_{prec}(s_p, v_l) + t_{sens}(s_l, v_p)}
cldice(vp,vl)=tprec(sp,vl)+tsens(sl,vp)2×tprec(sp,vl)×tsens(sl,vp)
dice的变化
图2说明了cl-x-dice的变化。我们的方法将管状结构视为具有可变半径的实体:利用沿中心线的法向圆来表示2d中的绘图线段,使用沿3d中的中心线对齐的圆形截面。这种对齐通过集合基方法促进体积估计。集合
d
d
d 表示从掩码点(
v
i
v_i
vi )到其各自边界的最小距离,定义为
d
=
{
d
i
;
v
i
∣
i
∈
[
1
,
q
]
,
j
∈
[
1
,
k
]
}
d = \{d_i; v_i | i \in [1,q], j \in [1,k]\}
d={di;vi∣i∈[1,q],j∈[1,k]} ,形成距离图。集合
r
r
r ,与骨架点
s
s
s 相关,定义为
r
=
{
r
i
;
s
i
∣
i
∈
[
1
,
n
]
,
j
∈
[
1
,
m
]
}
r = \{r_i; s_i | i \in [1,n], j \in [1,m]\}
r={ri;si∣i∈[1,n],j∈[1,m]} ,表示每个骨架点(
s
s
s )与其骨架半径(
r
r
r )的距离。
s
s
s 中的每个骨架点的半径由距离图
d
d
d 派生,生成集合
r
r
r 。相反,集合
t
=
{
t
i
;
b
j
s
∣
i
∈
[
1
,
n
]
,
j
∈
[
1
,
m
]
}
t = \{t_i; b_j^s | i \in [1,n], j \in [1,m]\}
t={ti;bjs∣i∈[1,n],j∈[1,m]} 表示骨架半径的集合,表示在
s
s
s 中的骨架点。
d
,
r
,
t
d, r, t
d,r,t 是
r
n
\mathbb{r}^n
rn 的元素。为了协调骨架线和距离图计算中的差异,超出
r
max
r_{\max}
rmax 的
d
d
d 中的值被调整为
r
max
r_{\max}
rmax 。因此,
r
r
r 的范围为
[
0
,
r
max
]
[0, r_{\max}]
[0,rmax] 且
d
d
d 的范围为
[
1
,
r
max
]
[1, r_{\max}]
[1,rmax] 。对于 p 个掩码点
{
v
i
∣
i
∈
z
i
∈
[
1
,
p
]
}
\{v_i | i \in \mathbb{z}_{i \in [1,p]}\}
{vi∣i∈zi∈[1,p]} ,在2d平面上与中心线或3d截面中的点的距离
d
i
d_i
di ,骨架半径
r
r
r 范围在 [1, r] 之内。cl-x-dice度量设计用于解决不同直径血管的分割挑战:
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
=
∣
q
s
p
∩
q
v
l
∣
∣
q
s
p
∣
t_{prec}(s_p, s_l, v_l) = \frac{|q_{sp} \cap q_{vl}|}{|q_{sp}|}
tprec(sp,sl,vl)=∣qsp∣∣qsp∩qvl∣
t
s
e
n
s
(
s
l
,
v
p
)
=
∣
q
l
∩
q
v
∣
∣
q
l
∣
t_{sens}(s_l, v_p) = \frac{|q_{l} \cap q_{v}|}{|q_{l}|}
tsens(sl,vp)=∣ql∣∣ql∩qv∣
cl-x-dice
(
v
p
,
v
l
)
=
2
×
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
×
t
s
e
n
s
(
s
l
,
v
p
)
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
+
t
s
e
n
s
(
s
l
,
v
p
)
\text{cl-x-dice}(v_p, v_l) = \frac{2 \times t_{prec}(s_p, s_l, v_l) \times t_{sens}(s_l, v_p)}{t_{prec}(s_p, s_l, v_l) + t_{sens}(s_l, v_p)}
cl-x-dice(vp,vl)=tprec(sp,sl,vl)+tsens(sl,vp)2×tprec(sp,sl,vl)×tsens(sl,vp)
我们定义
u
u
u 为每个元素为1的
r
n
\mathbb{r}^n
rn 。我们引入变量
q
s
p
,
q
s
l
,
q
v
l
,
q
p
q_{sp}, q_{sl}, q_{vl}, q_{p}
qsp,qsl,qvl,qp 来解决几何和血管直径不平衡在分割过程中提出的不同方面。这些变量对于血管结构的详细分析至关重要。表1中提供了cl-x-dice在血管分割中的综合比较。q的关键符号定义为:sp = sp, sl = sl, vl = vl, vp = vp, s = sl, v = vl 和 spp = sp \cap vp。此外,归一化比率表示为
r
n
=
r
r
max
r_n = \frac{r}{r_{\max}}
rn=rmaxr ,面积比
s
n
=
s
p
v
p
s_n = \frac{s_p}{v_p}
sn=vpsp ,以及
d
n
=
d
r
max
d_n = \frac{d}{r_{\max}}
dn=rmaxd 。图3展示了不同度量对平移、变形和直径不平衡的响应。我们广泛分析了cl-x-dice度量对几何变换的理论响应。详细证明见补充材料。
表1. cl-x-dice的逐步演变和2d与3d度量的比较。
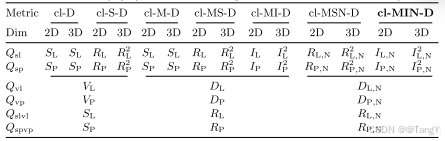
缩写包括参考(l),预测(p),中心线(cl),dice(d),骨架(s),掩码(m),逆骨架半径(i),归一化(n),和中心线边界(cb)。在这项研究中,cl-min-d等同于cb-d。
3 实验
3.1 数据集
我们在三个血管分割数据集上评估我们提出的方法。drive数据集【19】是二维视网膜血管成像的基准,包含40张彩色眼底照片(584x565像素),分为16张训练图像、4张验证图像和20张测试图像。对于三维ct肺动脉分割,miccai 2022 parse挑战数据集【8】包含100个ct扫描(512x512x228到512x512x376像素),其中80个用于训练,20个用于验证和测试。最后,miccai 2023 topcow挑战数据集【26】包括90个脑mra病例(大约481x586x185像素),其中72个用于训练,18个用于验证和测试。
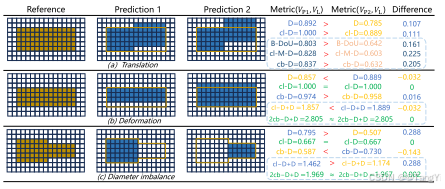
图3. (a) 在仅有平移扰动的情况下,cb-dice度量对cl-m-dice变化的敏感性,随着平移距离的增加,与b-dou相当,而cldice保持不变。 (b) 在均匀缩放(放大或缩小)中,cbdice度量确保了比cldice更一致的评估,能有效适应尺度变化。 © 对于直径不平衡,cbdice一致地评估了各种直径变化,优于cldice。
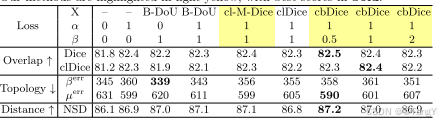
表2. 经过20个周期的训练后,使用nuu-net在drive数据集上的结果比较。我们的方法以浅黄色突出显示,最佳分数以粗体显示。
3.2 设置
我们使用pytorch 2.1进行实验,利用nvidia v100以提高计算效率。所有实验都是从头开始在nnu-net v2框架上训练的【5】。在标准化我们的实验设置时,我们选择不使用深度监督,将批量大小设置为2,并根据每个数据集的默认配置调整nnu-net的其他参数。此外,对于topcow 2023数据集,我们禁用了镜像增强,以防止左右标签的错误翻转。我们严格评估了cbdice损失在topcow 2023挑战和其他最近研究的分割模型上的效果。这项评估包括nnu-net【5】、swinunetr【3】和nextou【16】。比较研究涉及多种损失函数:标准dice损失、cldice损失【17】、b-dou损失【21】以及我们提出的cl-m-dice和cbdice损失。分割性能通过关键指标评估,如重叠(dice和cldice【17】)、拓扑(betti数误差和betti匹配误差【20】)和距离(归一化表面距离(nsd)在1.0mm容差内,参考【12,10】)。我们采用了在【11】中描述的可证明的差分骨架提取算法,并通过cucim库实现了加速的欧几里得距离变换。与nnu-net保持一致,我们使用交叉熵(ce)损失。损失函数定义为: l = 0.5 × c e + α 2 ( α + β ) × d i c e + β 2 ( α + β ) × x l = 0.5 \times ce + \frac{\alpha}{2(\alpha + \beta)} \times dice + \frac{\beta}{2(\alpha + \beta)} \times x l=0.5×ce+2(α+β)α×dice+2(α+β)β×x其中,x表示cl-x-dice或b-dou【21】。参数α和β是非负数;当两者都设置为0时,恢复为ce损失。
3.3 结果
我们的方法在二维和三维二值分割任务中展示了有效性。表2中详细分析的drive数据集结果表明,cbdice损失显著提高了重叠指标。具体来说,它实现了82.5%的最高dice得分和82.4%的cldice得分。此外,β = 0.5的cbdice变体达到87.2%的最高nsd。在parallel中,cl-m-dice与b-dou的表现相当。在parse 2022数据集中,cbdice损失在保持拓扑和几何结构方面表现有效,提高了分割dice得分,增加了nsd得分,并减少了拓扑错误。

图4. topcow 2023数据集结果的比较可视化。黄色箭头标记了分割的假阴性区域,绿色箭头指示假阳性区域,红色箭头标识了分类错误的区域。
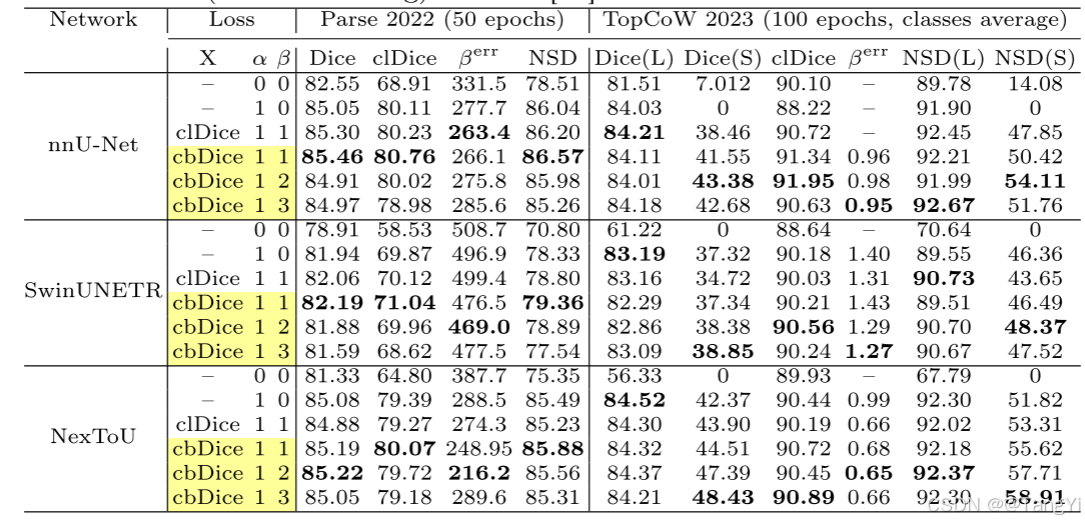
表3. parse 2022 和 topcow 2023 数据集结果的综合比较。这里,l 表示大动脉(不连通),s 表示小动脉(连通)。
4 结论
在本研究中,我们介绍了cbdice损失,这是cldice损失框架中的一项创新进展,并通过一系列cl-x-dice度量进一步阐述了这一进展。这些发展专门针对医学成像中血管分割的复杂性。对不同数据集的广泛评估验证了我们方法在保持拓扑完整性、捕获几何细节和在血管分割任务中保持平衡直径表示方面的有效性。与领先模型和损失函数的比较分析表明,cbdice损失在满足血管分割的复杂需求方面表现出了卓越的能力。
5. 补充材料
cldice变体的理论分析。 本节深入探讨了血管分割中cl-x-dice度量的理论基础和几何敏感性。我们引入了三个定理来阐明cl-x-dice度量的行为和计算:
定理 1
对于沿骨架线的垂直平移且无变形情况下,cl-m-dice系数对半径r内掩码
v
v
v的平移敏感,而cldice保持不变。
证明。 在二维中,cl-m-dice定义如下(类似地可扩展到三维):
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
=
∣
s
p
∩
d
l
∣
∣
r
p
∩
(
u
−
s
l
)
∣
+
∣
s
p
∩
r
l
∣
t_{prec}(s_p, s_l, v_l) = \frac{|s_p \cap d_l|}{|r_p \cap (u - s_l)| + |s_p \cap r_l|}
tprec(sp,sl,vl)=∣rp∩(u−sl)∣+∣sp∩rl∣∣sp∩dl∣
t
s
e
n
s
(
s
l
,
s
p
,
v
p
)
=
∣
s
l
∩
d
p
∣
∣
r
l
∩
(
u
−
s
p
)
∣
+
∣
s
l
∩
r
p
∣
t_{sens}(s_l, s_p, v_p) = \frac{|s_l \cap d_p|}{|r_l \cap (u - s_p)| + |s_l \cap r_p|}
tsens(sl,sp,vp)=∣rl∩(u−sp)∣+∣sl∩rp∣∣sl∩dp∣
在保持恒定半径的垂直平移下,
∣
s
p
∩
r
l
∣
|s_p \cap r_l|
∣sp∩rl∣等于
∣
s
l
∩
r
p
∣
|s_l \cap r_p|
∣sl∩rp∣。这将cl-m-dice的分母减少为
∣
r
p
∣
|r_p|
∣rp∣(对于
r
l
r_l
rl类似),使其敏感性仅依赖于分子。因此,cl-m-dice对
r
r
r内
v
v
v的空间位移作出反应。 相反,cldice评估
s
s
s和
v
v
v之间的重叠,不受这些变化的影响。
定理 2
cl-s-dice与cldice不同,对在无垂直平移下骨架变形的半径变化敏感。在完全重叠的情况下,cl-s-dice等于值为1的cldice。
证明。 在二维中,cl-s-dice定义如下(类似地可扩展到三维):
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
=
∣
r
p
∩
v
l
∣
∣
r
p
∣
,
t
s
e
n
s
(
s
l
,
s
p
,
v
p
)
=
∣
r
l
∩
v
p
∣
∣
r
l
∣
t_{prec}(s_p, s_l, v_l) = \frac{|r_p \cap v_l|}{|r_p|}, \quad t_{sens}(s_l, s_p, v_p) = \frac{|r_l \cap v_p|}{|r_l|}
tprec(sp,sl,vl)=∣rp∣∣rp∩vl∣,tsens(sl,sp,vp)=∣rl∣∣rl∩vp∣
对于cldice ≠ 1(部分重叠),半径的变化(
r
p
r_p
rp,
r
l
r_l
rl)影响
∣
r
p
∩
v
l
∣
|r_p \cap v_l|
∣rp∩vl∣和
∣
r
l
∩
v
p
∣
|r_l \cap v_p|
∣rl∩vp∣。具体来说,
s
=
{
s
i
,
b
j
s
∣
i
∈
[
1
,
n
]
,
j
∈
[
1
,
m
]
}
s = \{s_i, b_j^s | i \in [1,n], j \in [1,m]\}
s={si,bjs∣i∈[1,n],j∈[1,m]}和
r
=
{
r
i
;
s
i
,
b
j
s
∣
i
∈
[
1
,
n
]
,
j
∈
[
1
,
m
]
}
r = \{r_i; s_i, b_j^s | i \in [1,n], j \in [1,m]\}
r={ri;si,bjs∣i∈[1,n],j∈[1,m]},任何
s
i
s_i
si的
r
i
r_i
ri的变化修改cl-s-dice。 当cldice = 1(完全重叠),
∣
r
p
∩
v
l
∣
|r_p \cap v_l|
∣rp∩vl∣和
∣
r
l
∩
v
p
∣
=
∣
r
l
∣
|r_l \cap v_p| = |r_l|
∣rl∩vp∣=∣rl∣,cl-s-dice与cldice一致,突显了cl-s-dice在其他情况下对半径变化的敏感性。
定理 3
cl-x-dice增强了几何敏感性并补偿了直径差异,同时保留了cldice的拓扑完整性。
证明。 cl-x-dice度量通过引入变量
q
s
l
q_{sl}
qsl、
q
s
p
q_{sp}
qsp、
q
v
l
q_{vl}
qvl和
q
v
p
q_{vp}
qvp,提供了对几何变化(包括大小和形状变化)的高级敏感性,同时保持cldice的拓扑保留特性。
t
p
r
e
c
(
s
p
,
s
l
,
v
l
)
=
∣
q
s
p
∩
q
v
l
∣
∣
q
s
p
∩
q
s
p
v
p
∩
(
u
−
s
l
)
∣
+
∣
q
s
p
∩
q
s
l
v
l
∣
t_{prec}(s_p, s_l, v_l) = \frac{|q_{sp} \cap q_{vl}|}{|q_{sp} \cap q_{spvp} \cap (u - s_l)| + |q_{sp} \cap q_{slvl}|}
tprec(sp,sl,vl)=∣qsp∩qspvp∩(u−sl)∣+∣qsp∩qslvl∣∣qsp∩qvl∣
t
s
e
n
s
(
s
l
,
s
p
,
v
p
)
=
∣
q
s
l
∩
q
v
p
∣
∣
q
s
l
∩
q
s
l
v
l
∩
(
u
−
s
p
)
∣
+
∣
q
s
l
∩
q
s
p
v
p
∣
t_{sens}(s_l, s_p, v_p) = \frac{|q_{sl} \cap q_{vp}|}{|q_{sl} \cap q_{slvl} \cap (u - s_p)| + |q_{sl} \cap q_{spvp}|}
tsens(sl,sp,vp)=∣qsl∩qslvl∩(u−sp)∣+∣qsl∩qspvp∣∣qsl∩qvp∣
方程9和方程10代表了一种平衡的方法,在适应几何变化的同时保持拓扑准确性,从而在拓扑完整性和几何精度之间实现平衡。




发表评论