✅博主简介:热爱科研的matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:海神之光
🏆代码获取方式:
海神之光matlab王者学习之路—代码获取方式
⛳️座右铭:行百里者,半于九十。
更多matlab仿真内容点击👇
matlab图像处理(进阶版)
路径规划(matlab)
神经网络预测与分类(matlab)
优化求解(matlab)
语音处理(matlab)
信号处理(matlab)
车间调度(matlab)
⛄一、传统dwa算法
在传统的动态窗口法中,在模拟机器人的移动轨迹前,需要建立机器人的运动模型。图1为典型的移动机器人运动学模型示意图。
v (t)和w (t)分别代表了移动机器人在世界坐标系中的线速度和角速度。在每个采样周期内,对机器人的移动轨迹做近似化处理,将每个采样周期内的运动路径看作是直线,则t+1时刻的移动机器人位置(x (t+1),y (t+1))为
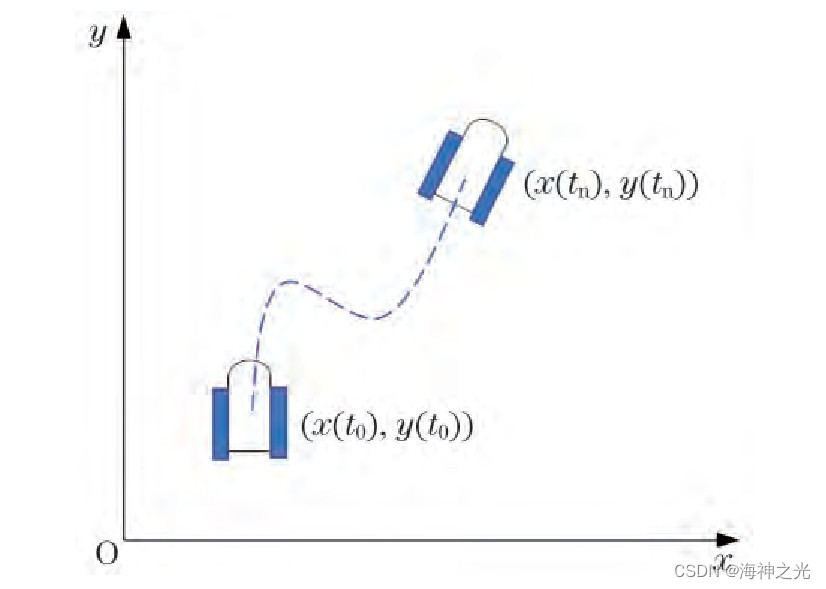
图1 典型移动机器人运动模型
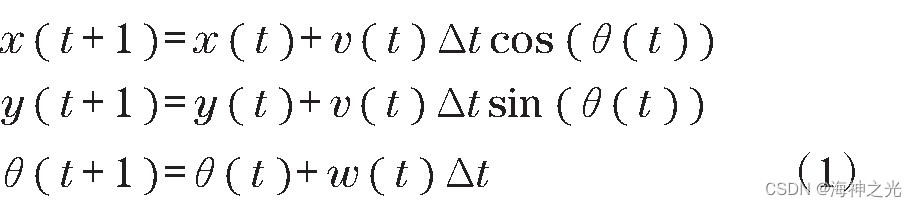
即移动机器人沿着方位角方向线性移动v (t)δt,其方位角相对于世界坐标系移动w (t)δt。
根据移动机器人的运动模型,在获取速度的基础上,就可以进行轨迹推算。因此,动态窗口法算法的两个核心分别是:(1)根据障碍物环境及机器人自身的机械特性等形成速度约束,生成动态窗口进行速度采样。(2)依据评价函数,对所采样的速度相应的预测轨迹进行评分,从而获取最优路径并执行。
速度采样时,移动机器人的速度主要受如下约束:
(1)移动机器人受自身最大、最小速度的限制,也是dwa算法求解速度的最大范围vi:
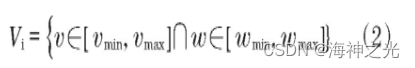
(2)受移动机器人自身电机的影响,其增速降速提供的力矩有限,因此,在模拟机器人前向移动的周期内,存在动态窗口,即该窗口内的速度是机器人在自身机械特性影响下所能实现的实际速度vj:

(3)为了实现安全避障,不与占据一定空间的障碍物发生碰撞,在减速最大加速度条件下可得范围vk,进一步缩小动态窗口范围:
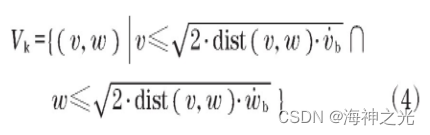
式中:dist (v,w)为相应速度的预测轨迹上的障碍物距离最小值。
综上,根据机器人自身的机械特性和障碍物环境,可以定义动态窗口为
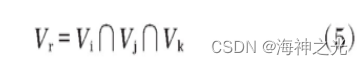
动态窗口中的采样轨迹如图2所示。运动轨迹主要是根据移动机器人每个线速度角速度的采样点以及前向仿真时间tsim生成的。
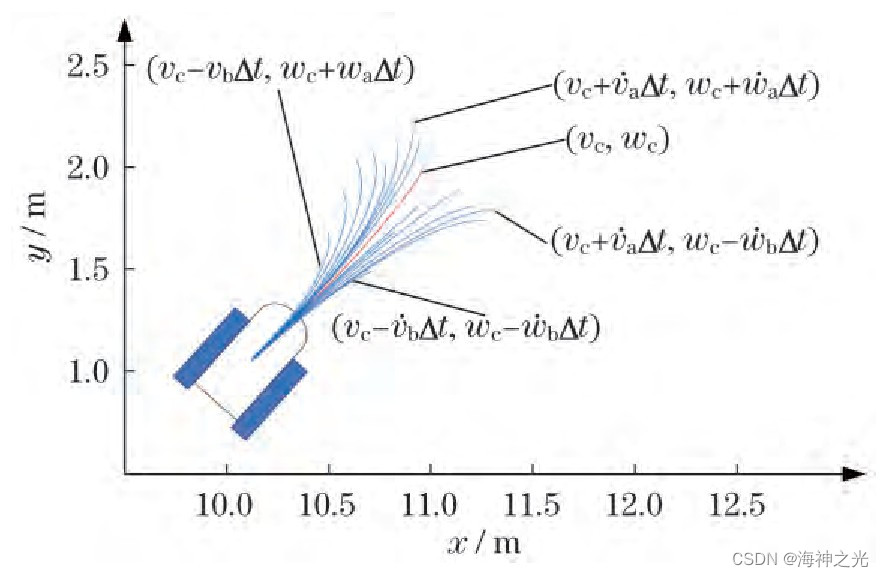
图2 动态窗口采样轨迹
获取移动机器人运动轨迹以后,需要评价函数对各个路径进行评分,选取其中分值最高的作为综合最优路径并执行:
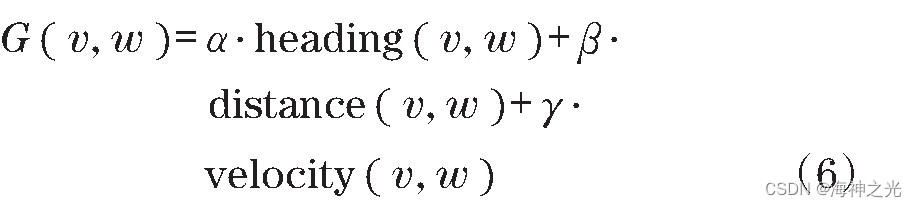
式中:heading (v,w)为偏转角评价子函数,该子函数的作用是评价在该模拟轨迹速度下的轨迹末端方向与目标点之间的角度差,其公式为180°-θ(θ越小,得分越高,其中,θ为所采样轨迹末端点朝向与机器人和目标点连线的夹角),该子函数主要作用是促进移动机器人在运动过程中其方位角不断朝向目标点;distance (v,w)为安全系数评价子函数,该子函数的作用是剔除掉有可能与障碍物发生碰撞或者接触的采样路径,实现移动机器人的安全避障,为避免该评价函数占比过大,对没有障碍物的采样路径进行评分时,安全系数评价子函数设定为常数;velocity (v,w)为速度评价子函数,该子函数的作用是在可以实现安全避障的采样轨迹中,选择出速度最快的路径,以尽快到达目标点。
⛄二、部分源代码
clc;
clear;
close all;
%% problem definition
model=createmodel();
%@(x) 变量名 = @(输入参数列表)运算表达式
%它既是一种可用于传参和赋值的变量,又可以作为函数名使用。
% pso函数 这个x是 第x个粒子群
costfunction=@(x) mycost(x,model); % cost function 适应度函数
nvar=model.n; % number of decision variables 决策变量数量 10个位置点
varsize=[1 nvar]; %[1 10] % size of decision variables matrix 决策变量矩阵的大小
varmin.x=model.xmin; % lower bound of variables
varmax.x=model.xmax; % upper bound of variables
varmin.y=model.ymin; % lower bound of variables
varmax.y=model.ymax; % upper bound of variables
%% pso parameters
%迭代次数
maxit=300; % maximum number of iterations 500
%种群规模(群体规模)
npop=150; % population size (swarm size)
w=1; % inertia weight
wdamp=0.98; % inertia weight damping ratio
c1=1.5; % personal learning coefficient
c2=1.5; % global learning coefficient
%定义速度可行域
alpha=0.1;
velmax.x=alpha*(varmax.x-varmin.x); % maximum velocity
velmin.x=-velmax.x; % minimum velocity
velmax.y=alpha*(varmax.y-varmin.y); % maximum velocity
velmin.y=-velmax.y; % minimum velocity
%% initialization
% create empty particle structure
empty_particle.position=[];
empty_particle.velocity=[];
empty_particle.cost=[];
empty_particle.sol=[];
%结构体里的结构体
empty_particle.best.position=[];
empty_particle.best.cost=[];
empty_particle.best.sol=[];
% initialize global best
globalbest.cost=inf;
% create particles matrix 创建粒子矩阵 维度(npop,1)
particle=repmat(empty_particle,npop,1);
for i=1:npop
%i = 1的时候 等距离生成3个点 后面的就随机生成
% initialize position
if i > 1 %安排后面那些位置信息
particle(i).position=createrandomsolution(model);
else
% straight line from source to destination 从源到目标的直线
%linspace ==> 在初始点目标点之间等距离生成 n+2(12个点包括初始点和目标点)
xx = linspace(model.xs, model.xt, model.n+2);
yy = linspace(model.ys, model.yt, model.n+2);
%把10个点的信息传给particle
particle(i).position.x = xx(2:end-1);
particle(i).position.y = yy(2:end-1);
end
% initialize velocity 速度赋0 varsize=[1,10] zeros(varsize) ==> zeros(1,10)
% 相当于返回一个1x10的全零矩阵
particle(i).velocity.x=zeros(varsize);
particle(i).velocity.y=zeros(varsize);
% evaluation 返回路径长度cost(如果违反约束需要加上那一部分)和 sol(拟合点 距离 容忍度? 可靠性)
[particle(i).cost, particle(i).sol]=costfunction(particle(i).position);
% update personal best 更新个体数据
particle(i).best.position=particle(i).position;
particle(i).best.cost=particle(i).cost;
particle(i).best.sol=particle(i).sol;
% update global best 更新全局数据
if particle(i).best.cost<globalbest.cost
globalbest=particle(i).best;
end
end
⛄三、运行结果
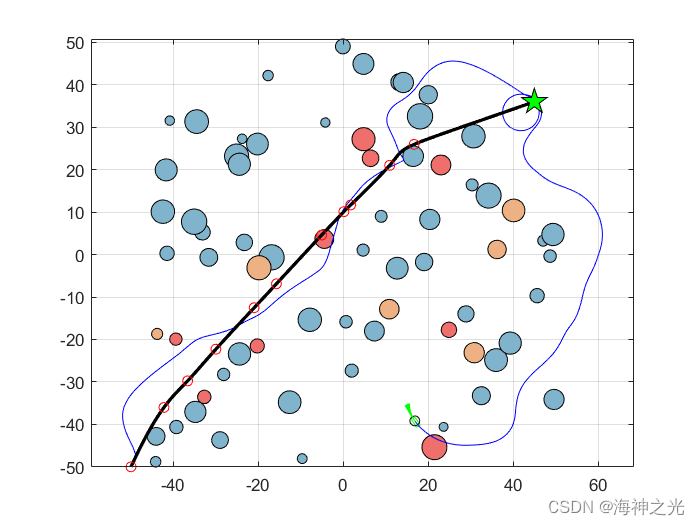
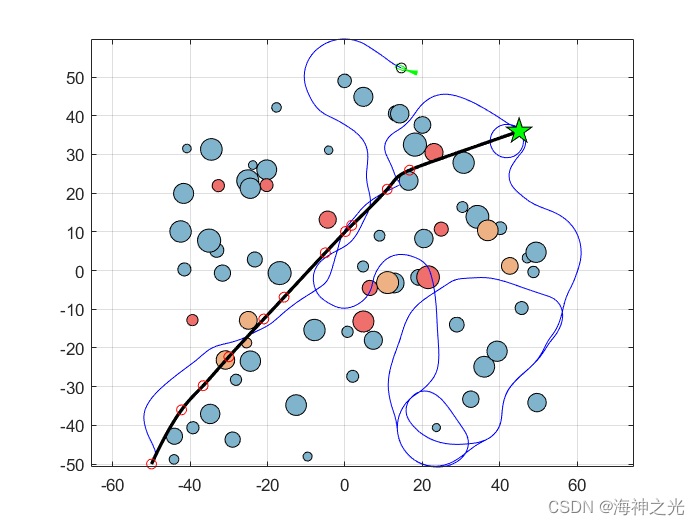
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]卞永明,季鹏成,周怡和,杨濛.基于改进型dwa的移动机器人避障路径规划[j].中国工程机械学报. 2021,19(01)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
🍅 仿真咨询
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(cnn)、lstm、支持向量机(svm)、最小二乘支持向量机(lssvm)、极限学习机(elm)、核极限学习机(kelm)、bp、rbf、宽度学习、dbn、rf、rbf、delm、xgboost、tcn实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、pm2.5浓度预测、电池健康状态预测、水体光学参数反演、nlos信号识别、地铁停车精准预测、变压器故障诊断
3 图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
4 路径规划方面
旅行商问题(tsp)、车辆路径问题(vrp、mvrp、cvrp、vrptw等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
5 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配
6 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、dv-hop定位优化、leach协议优化、wsn覆盖优化、组播优化、rssi定位优化
7 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
8 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
9 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
10 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合


发表评论