【排序算法】选择排序（C语言）_C/C++

【排序算法】—— 选择排序

一、选择排序的原理

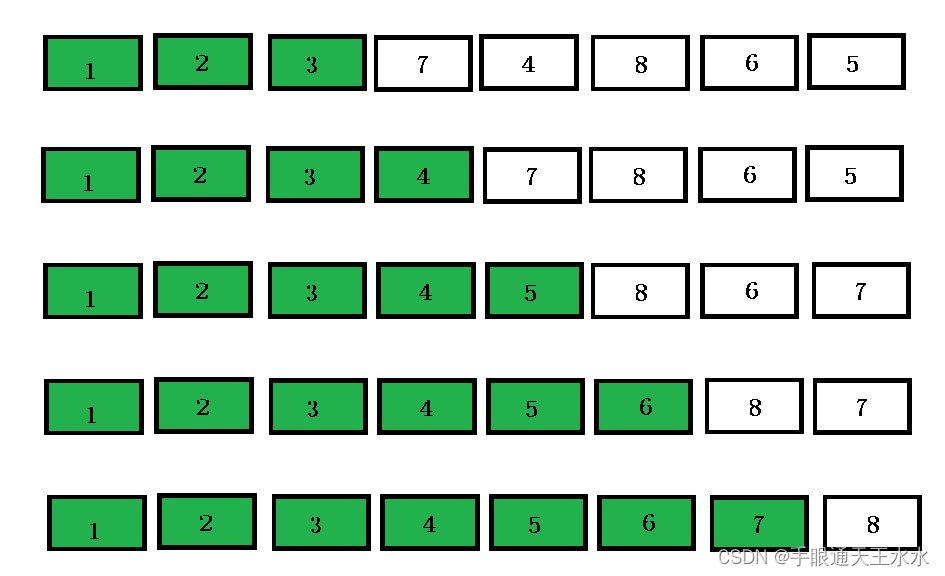
选择排序算法是通过遍历数组，选择出数组的最小或最大值，与指定位置交换数据，遍历完整个数组的所有位置就完成排序

遍历第一趟数组，找出数组的最小值，与第一个数据交换

选择排序1

选择排序2

遍历第二趟数组，继续找出最小值，与第二个数据交换

选择排序3

选择排序4

重复上述动作，遍历完数组就得到一个有序数组

选择排序5

二、选择排序的代码实现

//交换两个数据
void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

//选择排序
void selectsort(int* arr, int size)
{
	int i = 0;
    for (i = 0; i < size-1; i++)
    {
        int min = i;
        int j = 0;
        for (j = i+1; j < size; j++)
        {
            if (arr[j] < arr[min])
            {
                min = j;
            }
        }
        swap(&arr[i], &arr[min]);
    }
}

三、选择排序的优化

1. 优化思路

以上算法是每次找出最小的放在指定位置，一共要找n-1次，如果我们每次不但找到最小的，还找到最大的，将最小的与左端交换，最大的与右端交换，那么就少了一半的遍历次数，从而提高效率

变量begin和变量end是数组的两端，min和max分别找小和大的下标

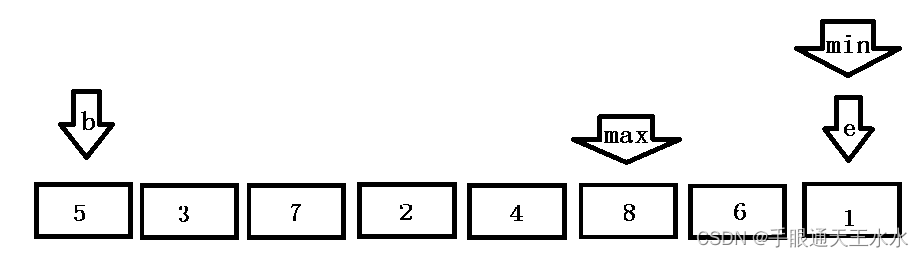
选择排序优化1

先交换min与begin位置的数值，再交换max与end位置的数值

选择排序优化2

begin右移，end左移，继续找大找小，继续交换

选择排序优化3

选择排序优化4

重复上述操作，直到遍历完所有数组

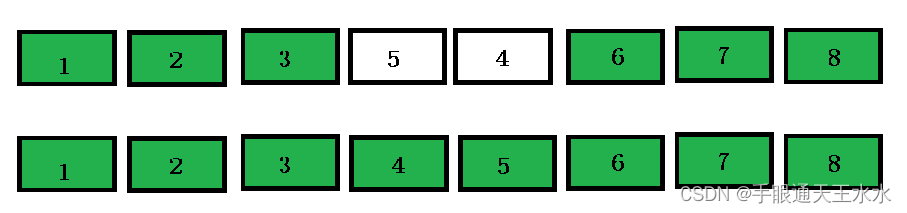
选择排序优化5

2. 排序优化后问题

若是max的位置与begin重合，则begin先与min的位置交换，此时max位置的最大值被交换走，导致end与max交换的数值是错误的

max与begin重合

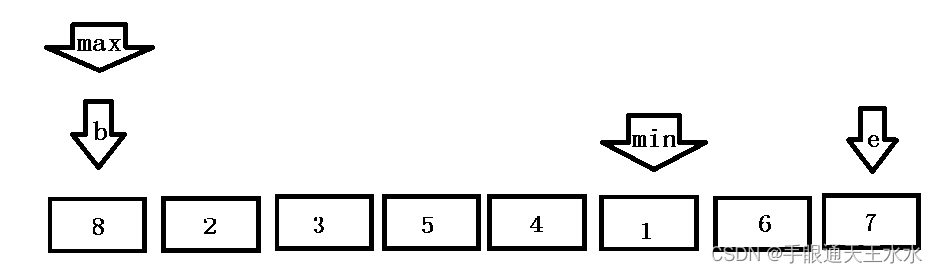
选择排序优化问题1

begin先与min的位置交换数据，此时max位置的已经不是最大值了

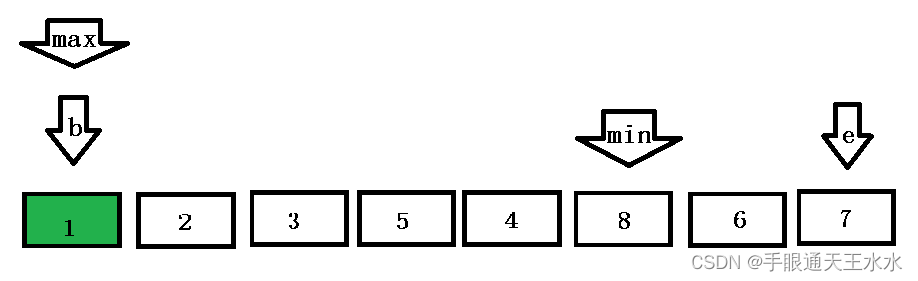
选择排序优化问题2

max再与end位置交换数据，排序就发生了错误

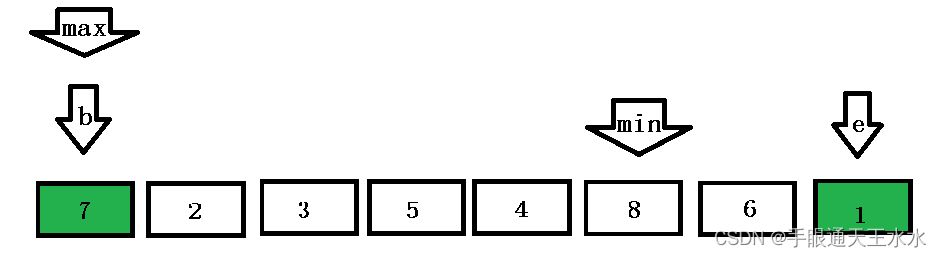
选择排序问题优化3

如何解决问题呢？

当max与begin重合时，begin与min交换后导致max指向的不再是最大值，所以当我们对begin交换后，就要对max进行一个修正，让max指向最大值，然后完成end的交换

max与begin重合，并且begin此时完成了交换，此时最大值已经交换到了min所指向的位置

选择排序优化问题4

对max进行修正并完成与end的交换

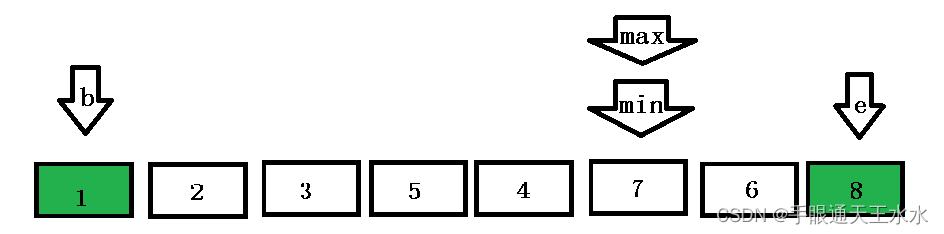
选择排序优化问题5

3. 优化代码的实现

//交换两个数据
void swap(int* a, int* b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

//选择排序
void selectsort(int* arr, int size)
{
	int begin = 0;
    int end = size - 1;
    while (begin < end)
    {
        int max = begin;
        int min = begin;
        int i = 0;
        for (i = begin+1; i <= end; i++)
        {
            if (arr[i] < arr[min])
            {
                min = i;
            }
            
            if (arr[i] > arr[max])
            {
                max = i;
            }
        }
        
        swap(&arr[begin], &arr[min]);
        if (begin == max)				//修正max
        {
            max = min;
        }
        swap(&arr[end], &arr[max]);
        
        begin++;
        end--;
    }
}