今天更新第一节信号分类,这一节我是结合了《数字信号处理》(第四版)这本书是我心目中的神作。建议大家有兴趣的抓紧入手,反复阅读。
第一、多维信号和多通道信号
多维信号: 多维信号指的是在多个维度上具有信息的信号。这些维度可以是时间、空间、频率等。通俗来讲,多维信号就相当于是去在看电影一样,电影的每一帧(信号)都是在时间这个维度上播放的,电影的每一帧也被框在具有长宽的屏幕里,这就是在空间维度展开的。3d电影是在这些的基础上加了深度这一维度。
多通道信号 :多通道信号通常指的是在多个独立通道上同时传输或记录的信号。这些通道可以是不同的传感器、不同的信号源或不同的信号处理路径。通俗来讲,多通道信号就是一个乐队的合奏,比方说这个合奏出来的乐曲(信号)是由钢琴小提琴(不同通道)等等组成的。
%% 多维信号
% 定义信号的维度大小
x = 0:0.1:10; % 一个维度的采样点
y = 0:0.1:10; % 另一个维度的采样点
% 创建二维网格
[x, y] = meshgrid(x, y);
% 生成二维正弦波信号
z = sin(x) + cos(y);
% 显示结果
figure;
surf(x, y, z); % 绘制三维曲面图
colormap('jet'); % 设置颜色图
shading interp; % 平滑着色
title('二维正弦波信号');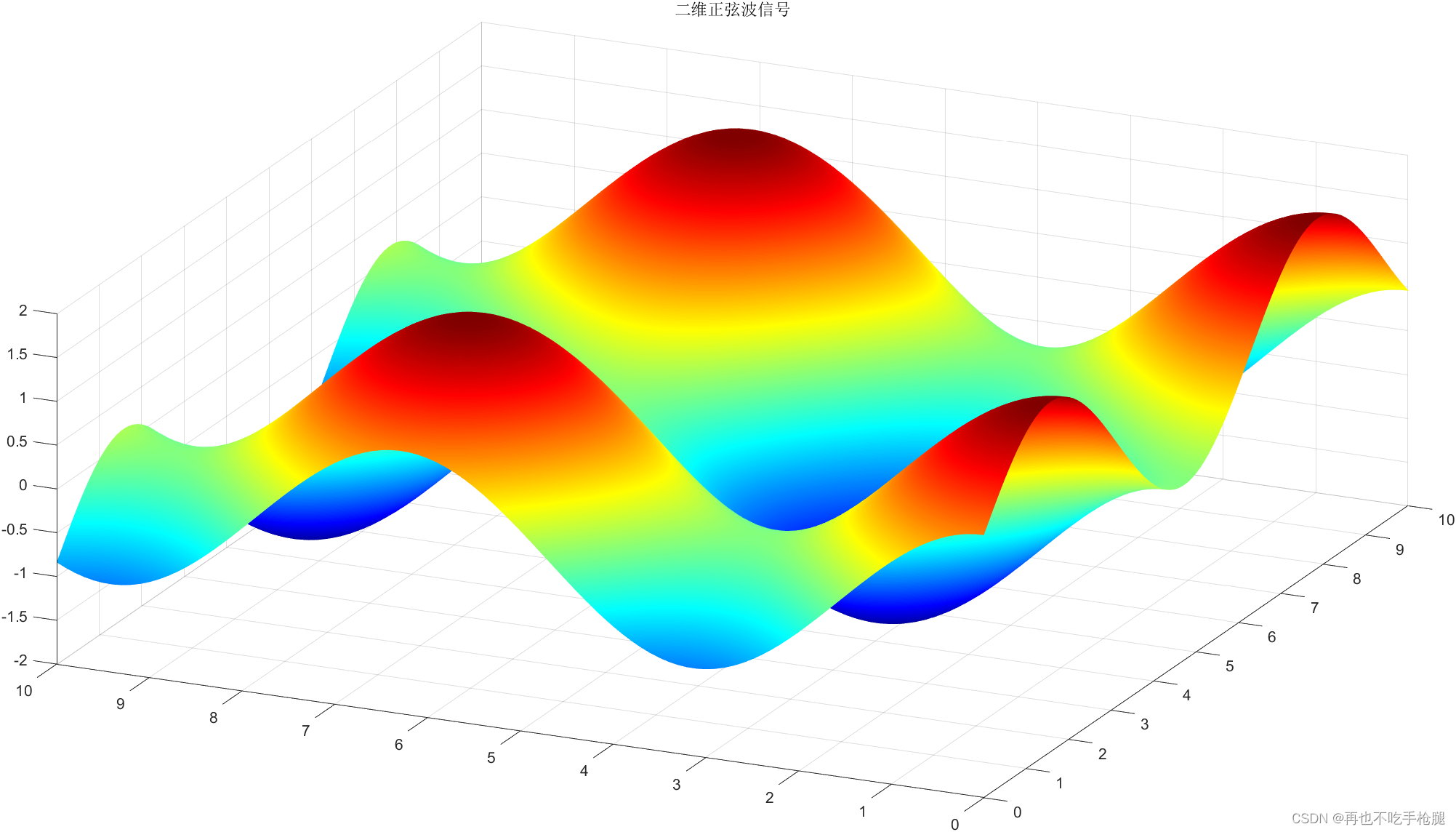
%% 多通道信号
% 定义采样率和信号长度
fs = 44100; % 采样率,单位hz
t = 0:1/fs:1-1/fs; % 时间向量,1秒长
% 生成两个通道的信号
channel1 = sin(2 * pi * 440 * t); % 440hz的正弦波,通道1
channel2 = 0.5 * sin(2 * pi * 550 * t + pi/4); % 550hz的正弦波,通道2,相位偏移
% 显示结果
figure;
subplot(2,1,1);
plot(t, channel1);
title('通道1信号');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(2,1,2);
plot(t, channel2);
title('通道2信号');
xlabel('时间 (秒)');
ylabel('幅度');
% 播放多通道信号
sound([channel1, channel2], fs);这是一段音频,自行播放。
第二、连续时间信号和离散时间信号
连续时间信号: 一个信号如果其定义域是连续的,即可以在任意时间点t(通常是实数)上取值,则称该信号为连续时间信号。
离散时间信号:一个信号如果其定义域是离散的,即只在一系列分离的、通常等间隔的时间点n(通常是整数)上取值,则称该信号为离散时间信号。
这个都很好理解,连续和离散也都是数学概念。
我给出《数字信号处理》(第四版)中的图,帮助更好理解离散时间信号。
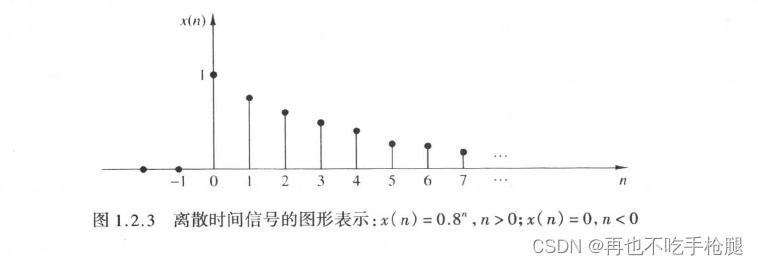
在离散点上选择模拟信号值。(也叫做我们上一节讲过的采样,后面还会详细介绍的)
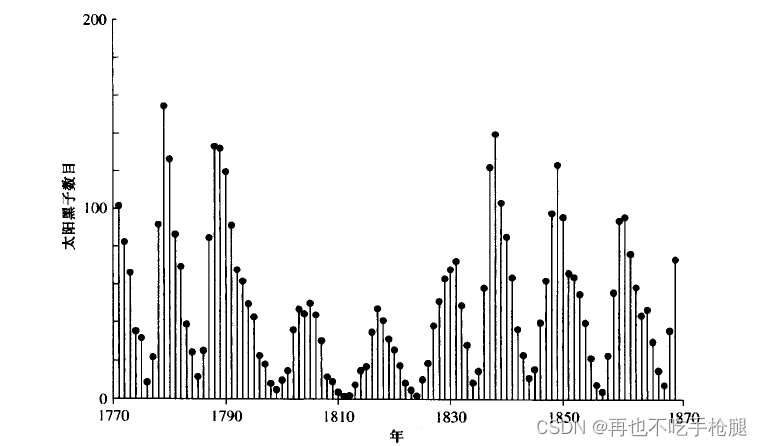
通过一段时间内累积某种变量。类似上图这种。
第三、 连续值信号和离散值信号(一种取值特性)
连续值信号:这类信号的取值可以是连续的,即在某个范围内可以取任意实数值。例如,温度计的读数可以是任意小数点后的值,没有固定的离散值限制。
离散值信号:这类信号的取值是离散的,即它们只能取一组特定的数值,而不是任意实数。例如,数字钟的显示只能显示整数,如1, 2, 3, ...,而不能显示1.5或2.75这样的值。
然而,这两个术语有时会与“连续时间信号”和“离散时间信号”混淆。为了清晰起见,我们通常使用以下术语:
- 连续时间连续值信号(continuous-time continuous-valued signal):信号的取值和时间都是连续的,如模拟音频信号。
- 连续时间离散值信号(continuous-time discrete-valued signal):信号的时间是连续的,但取值是离散的,这种情况比较少见,因为如果时间连续,取值通常也是连续的。
- 离散时间连续值信号(discrete-time continuous-valued signal):信号的时间是离散的,但取值是连续的,这种情况也相对少见,因为离散时间通常意味着取值也是离散的。
- 离散时间离散值信号(discrete-time discrete-valued signal):信号的时间和取值都是离散的,如数字音频信号,它在特定的时间点取特定的整数值。
第四、 确定性信号与随机性信号
确定性信号:如果一个信号的行为可以通过一组确定的规则或数学方程完全描述,那么这个信号就是确定性信号。
随机性信号:如果一个信号的行为不能通过确定的规则完全描述,并且包含随机性或不确定性,那么这个信号就是随机性信号。
混合信号: 在实际应用中,很多信号既包含确定性成分也包含随机性成分。例如,一个电子设备的输出信号可能包含一个确定性的正弦波信号和一个随机的噪声成分。这种信号被称为混合信号,需要结合确定性和随机性信号的处理方法来分析。
这里就不得不说一下一些比较重要的内容了,方便接下里的学习
随机信号通常需要结合概率论和统计学办法进行描述(数学描述,也是时间特征提取的一种角度)如概率密度函数、均值、方差等。以下是一个高斯分布的随机信号与它的数学描述。
%% 高斯分布的随机信号与其数学描述
% 参数定义
mu = 0; % 均值
sigma = 1; % 标准差
n = 1000; % 信号长度
% 生成随机信号
t = (0:n-1)/10; % 时间向量,假设采样频率为10hz
signal_gaussian = mu + sigma * randn(1, n); % 高斯分布随机信号
% 绘制信号
figure;
plot(t, signal_gaussian);
title('gaussian random signal');
xlabel('time (seconds)');
ylabel('amplitude');
grid on;
% 绘制信号的直方图
figure;
histogram(signal, 50, 'normalization', 'pdf');
title('histogram of uniform random signal');
xlabel('value');
ylabel('probability density');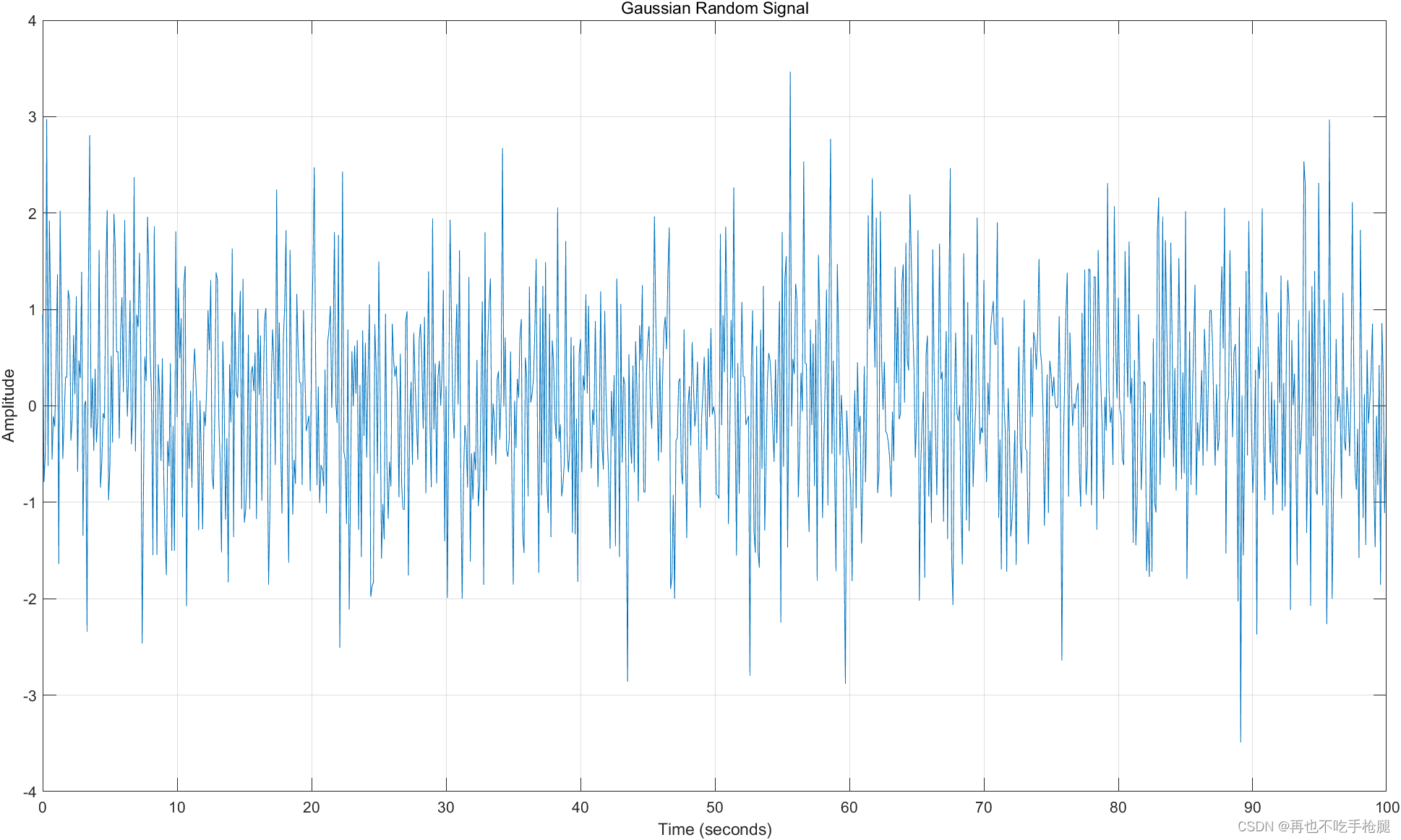

声明
这次因为只是生成了一些模拟的信号,所以就没有给出python代码,大家可以参照matlab复现python代码(虽然无意义还浪费时间)。
如有侵权,联系作者,作者会进行删除的。


发表评论