机器学习——线性回归之Ridge回归和Lasso回归_Python

机器学习——线性回归之ridge回归和lasso回归

线性回归是一种常见的机器学习算法，用于建模自变量和因变量之间的线性关系。在实际应用中，除了普通的线性回归外，还有两种常见的改进方法，即ridge回归和lasso回归。本文将简单介绍ridge回归和lasso回归的理论基础python代码实现进行对比分析。

线性回归

线性回归是一种用于预测连续型因变量的机器学习算法。其基本思想是利用自变量的线性组合来拟合因变量，假设我们有一个包含 $m$ 个样本的训练集 $x^{(i)}, y^{(i)})$ ，其中 $x^{(i)}$ 是自变量， $y^{(i)}$ 是因变量。线性回归模型可以表示为：

$h_{\theta}(x) = \theta^t x + b$

其中， $h_{\theta}(x)$ 表示模型预测值， $\theta$ 是模型参数向量， $x$ 是自变量， $b$ 是偏置项。

线性回归的损失函数通常选择平方损失函数：

$j(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2$

我们的目标是最小化损失函数 $j(\theta)$ ，通过梯度下降等优化算法求解参数 $\theta$ 。

ridge回归

ridge回归是线性回归的一种改进方法，通过在损失函数中引入l2正则化项，以减少模型的过拟合。其损失函数可以表示为：

$j(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n}\theta_j^2$

其中， $\lambda$ 是正则化参数，用于控制正则化项的权重。

lasso回归

与ridge回归类似，lasso回归也是线性回归的一种改进方法，通过在损失函数中引入l1正则化项来减少模型的过拟合。其损失函数可以表示为：

$j(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n}|\theta_j|$

与ridge回归不同的是，lasso回归使用了绝对值来惩罚参数的大小。

ridge回归与lasso回归的对比

相同点：
- ridge回归和lasso回归都是线性回归的改进方法，通过引入正则化项来减少模型的过拟合。
- 两者都可以用于处理高维数据集，并且可以同时考虑多个特征之间的关系。
不同点：
- 正则化项的不同：ridge回归使用l2正则化项，lasso回归使用l1正则化项。
- 参数选择的影响：lasso回归的l1正则化项可以使得部分参数变为0，因此可以实现特征选择的作用；而ridge回归的l2正则化项只能使参数趋近于0，但不会真正取到0。

案例分析

为了更直观地比较ridge回归和lasso回归的效果，我们使用一个包含噪声的线性数据集进行实验。我们将分别使用ridge回归和lasso回归模型对数据进行拟合，并绘制出拟合曲线和原始数据的对比图。

python代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import ridge, lasso
from sklearn.metrics import mean_squared_error

# 生成线性数据集
x, y = make_regression(n_samples=100, n_features=1, noise=20, random_state=42)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)

# 训练ridge回归模型
ridge_model = ridge(alpha=0.1)
ridge_model.fit(x_train, y_train)

# 训练lasso回归模型
lasso_model = lasso(alpha=0.1)
lasso_model.fit(x_train, y_train)

# 计算模型在测试集上的均方误差
ridge_pred = ridge_model.predict(x_test)
ridge_mse = mean_squared_error(y_test, ridge_pred)

lasso_pred = lasso_model.predict(x_test)
lasso_mse = mean_squared_error(y_test, lasso_pred)

print("ridge回归模型的均方误差：", ridge_mse)
print("lasso回归模型的均方误差：", lasso_mse)

# 绘制拟合曲线和原始数据的对比图
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', label='original data')
plt.plot(x_test, ridge_pred, color='red', label='ridge regression')
plt.plot(x_test, lasso_pred, color='green', label='lasso regression')
plt.title('comparison of ridge and lasso regression')
plt.xlabel('feature')
plt.ylabel('target')
plt.legend()
plt.show()

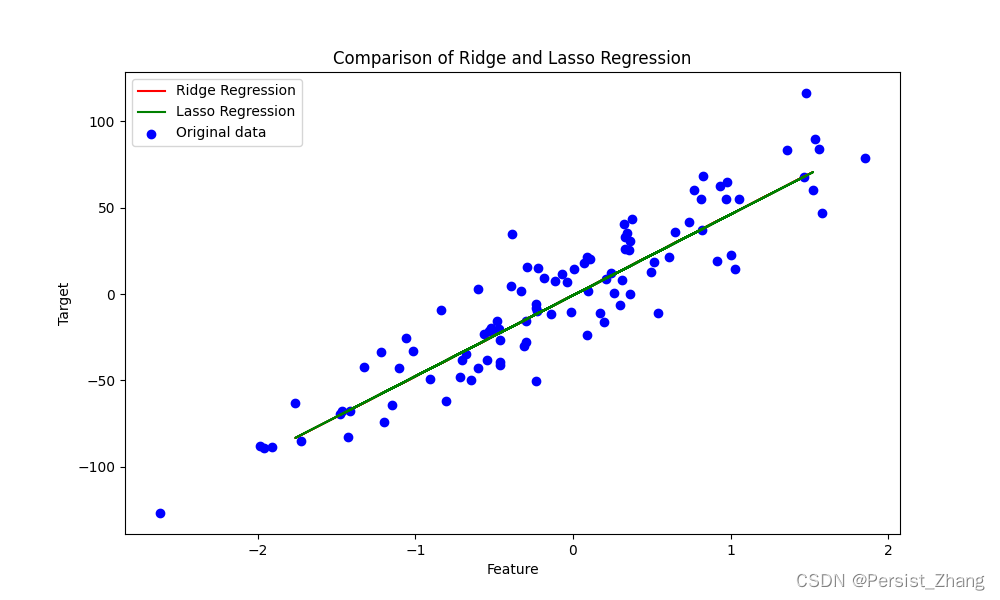
在这里插入图片描述

结果说明与结论

通过上述代码实现，我们分别训练了ridge回归和lasso回归模型，并绘制了拟合曲线和原始数据的对比图。从结果中可以看出，ridge回归和lasso回归都能够很好地拟合数据，并且在测试集上的均方误差也相对较小。但是，两者在拟合的曲线上略有不同，这是因为两种正则化项的不同导致了模型对参数的惩罚程度不同，从而影响了模型的拟合结果。总的来说，ridge回归和lasso回归都是有效的线性回归改进方法，可以根据具体的问题特点选择合适的模型进行建模。


验证码：

验证码：

机器学习——线性回归之Ridge回归和Lasso回归

2024年08月05日 • Python •我要评论