python图像处理实验：图像处理基本操作

实验一：图像处理基本操作

一、实验目的

1、熟悉并掌握matlab工具的使用；

2、实现图像的读取、显示、存储、平移、镜像、放大、缩小及旋转操作；

3、掌握常用的插值方法，并了解其优缺点。

二、实验环境

ide：pycharm

python

三、实验内容（题目、相关知识（函数，原理…）、代码、实验结果）

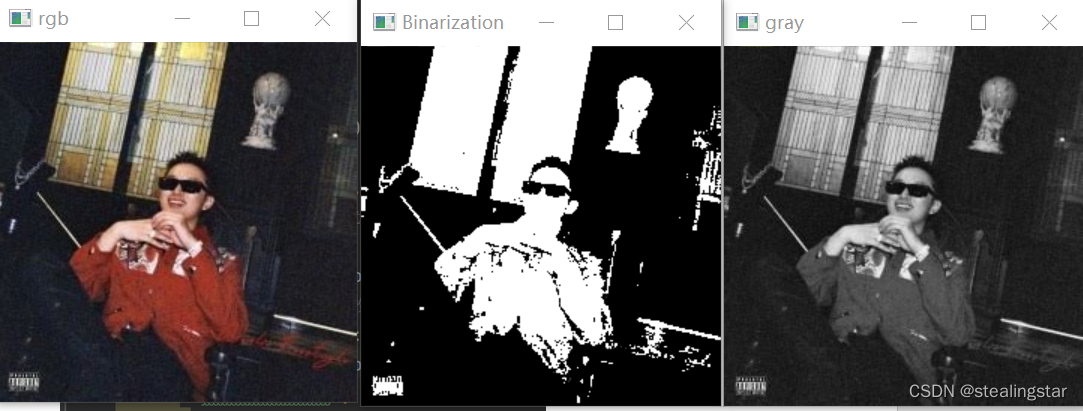
1、读入一幅rgb图像（自选），变换为灰度图像和二值图像，并在同一个窗口内分别显示rgb图像和灰度图像，注上文字标题,并将结果以文件形式存到磁盘上。

灰度变换属于空域变换增强技术。

目的：

一般成像系统形成图像的亮度有限，对比度不足，使图像的视觉效果差，灰度变换即可有效地改善视觉效果。

概念：

灰度变换是一种点操作，根据原始图像中每个像素的灰度值，按照某种映射规则将其转化为另一灰度值。灰度变换可有效改善图像的视觉效果，变换原理可表示为如式所示：

t = e(k)

式中：k为原始图像的灰度值f(x,y)，t为变换图像的灰度值g(x,y)，e()为灰度增强函数。

原理：

灰度变换原理可由图来说明，其中，图(a)为原始图像，具有两种灰度级，分别用b和w来表示；图(b)为灰度增强函数，根据函数的映射规则，原始图像的灰度值b映射为灰度值w，原始图像的灰度值w映射为灰度值b；图（c）为变换后的图像。

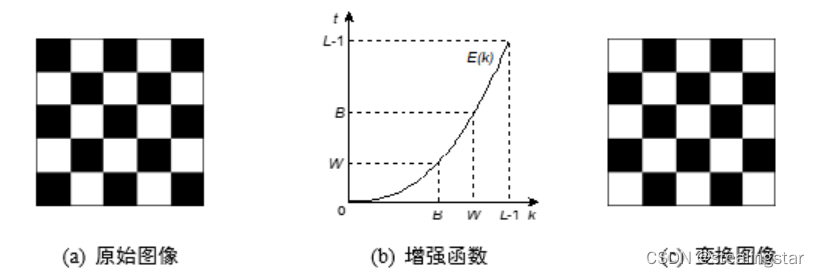
灰度变换的关键在于根据增强要求设计灰度映射规则，即设计灰度增强函数。典型灰度变换函数包括：比例线性变换、分段线性变换、非线性变换

图像二值化就是将图像上的像素点的灰度值设置为0或255，也就是将整个图像呈现出明显的黑白效果的过程。二值图像每个像素只有两种取值：要么纯黑，要么纯白。由于二值图像数据足够简单，许多视觉算法都依赖二值图像。通过二值图像，能更好地分析物体的形状和轮廓。二值图像也常常用作原始图像的掩模（又称遮罩、蒙版，mask）：它就像一张部分镂空的纸，把我们不感兴趣的区域遮掉。进行二值化有多种方式，其中最常用的就是采用阈值法（thresholding）进行二值化。

转换为灰度图像使用函数cvcolor，这里转化为二值图像直接设置阈值判断灰度值大小，如果灰度值大于阈值直接赋值为255，反之赋值为0

实验代码：

实验结果：

2、对图像（自选）执行平移、镜像（水平镜像、垂直镜像）放大、缩小及旋转操作，其中放大、旋转操作分别采用最近邻插值及双线性插值方法实现，要求根据算法自己编写代码实现，并分析两种插值方法的优缺点。

（1）平移

图像平移首先定义平移矩阵m，再调用warpaffine()函数实现平移，python函数如下：

m = np.float32([[1, 0, x], [0, 1, y]])

m表示平移矩阵，其中x表示水平平移量，y表示垂直平移量

shifted = cv2.warpaffine(src, m, dsize[, dst[, flags[, bordermode[, bordervalue]]]])

src表示原始图像

m表示平移矩阵

dsize表示变换后的输出图像的尺寸大小

dst为输出图像，其大小为dsize，类型与src相同

flag表示插值方法的组合和可选值

bordervalue表示像素外推法，当bordermode = border_transparent时，表示目标图像中的像素不会修改源图像中的“异常值”。

bordervalue用于边界不变的情况，默认情况下为0

平移后图像

（2）旋转

旋转前：

x0=rcosb，y0=rsinb

旋转后：

x1=rcos(b-a)=rcosbcosa+rsinbsina=x0cosa+y0sina

y1=rsin(b-a)=rsinbcosa-rcosbsina=-x0sina+y0cosa

一般3-d旋转的变换。将一个空间点p绕一个中心点c旋转可用连续的3个变换来实现：

第1个变换：平移点c到坐标原点。

第2个变换：将p绕原点旋转。

第3个变换：平移点c回到原始位置。

本实验中要求旋转采用双线性插值法

如下为主要算法代码：

import math
import random
import cv2
import numpy as np
def bilinear_rotate(imgarray):
    h, w, channel = imgarray.shape
    pi = math.pi
    theta = random.randint(0,360)
    angle = theta * pi / 180
    matrix1 = np.array([[1, 0, 0],
                        [0, -1, 0],
                        [-0.5 * h, 0.5 * w, 1]])
    matrix2 = np.array([[math.cos(angle), -math.sin(angle), 0],
                        [math.sin(angle), math.cos(angle), 0],
                        [0, 0, 1]])
    matrix3 = np.array([[1, 0, 0],
                        [0, -1, 0],
                        [0.5 * h, 0.5 * w, 1]])
    new_data = np.zeros_like(imgarray,dtype=np.uint8)
    for i in range(h):
        for j in range(w):
            dot1 = np.matmul(np.array([i, j, 1]), matrix1)
            dot2 = np.matmul(dot1, matrix2)
            dot3 = np.matmul(dot2, matrix3)
            new_coordinate = dot3
            new_i = int(math.floor(new_coordinate[0]))
            new_j = int(math.floor(new_coordinate[1]))
            u = new_coordinate[0] - new_i
            v = new_coordinate[1] - new_j
            if new_j>=w or new_i >=h or new_i<1 or new_j<1 or (i+1)>=h or (j+1)>=w:
                continue
            if (new_i + 1)>=h or (new_j+1)>=w:
                new_data[i, j, :] = imgarray[new_i,new_j, :]
            else:
                new_data[i, j, :] = (1-u)*(1-v)*imgarray[new_i,new_j, :] + \
                                   (1-u)*v*imgarray[new_i,new_j+1, :] + \
                                   u*(1-v)*imgarray[new_i+1,new_j, :] +\
                                   u*v*imgarray[new_i+1,new_j+1, :]
    return new_data
image = cv2.imread('asen.jpg')
new_image = bilinear_rotate(image)
cv2.imshow('rotated image', new_image)

运行结果：

（3）缩放

缩放采用最邻近插值缩放

插值的目的是根据已知的图像的像素值获得未知目标图像的像素值

其中src表示原始图像，tar表示插值得到的目标图像，h和w分别表示图像的高度和宽度。插值的核心是找到(tar_x, tar_y)和(src_x, src_y)的映射关系，从而实现对目标图像的每一个像素点进行赋值。假设目的是将原始图像长度和宽度扩大(3，4)倍，即：

ratio_h = tar_h/src_h = tar_x/src_x = 3

ratio_w = tar_w/src_w = tar_y/src_y = 4

通过上式变形，得到目标图像的像素点和原始图像的像素点映射如下：

tar_x = src_x/ratio_h

tar_y = src_y/ratio_w

知道了像素点之间的映射关系，实现算法就很容易了，算法流程如下：

根据tar_h和tar_w创建目标图像

计算缩放比例因子ratio

遍历目标图像每个像素点，计算映射关系

遍历目标图像每个像素点，使用对应原始图像的对应像素点对其赋值

算法代码：

import cv2
import numpy as np

def test(img, weight_out, height_out):
    # 获取图像的大小
    height_in, weight_in, _ = img.shape
    # 创建输出图像
    outimg = np.zeros((height_out, weight_out, 3), dtype=np.uint8)

    for x in range(height_out - 1):
        for y in range(weight_out - 1):
            # 计算输出图像坐标（i,j）坐标使用输入图像中的哪个坐标来填充
            x_out = round(x * (height_in / height_out))
            y_out = round(y * (weight_in / weight_out))
            # 插值
            outimg[x, y] = img[x_out, y_out]
    return outimg


# 读取图像
img = cv2.imread('asen.jpg')
test = test(img, int(img.shape[1] * 1.5), int(img.shape[0] * 1.5))
# opencv函数
opencv_test = cv2.resize(img, (int(img.shape[1] * 1.5), int(img.shape[0] * 1.5)))

cv2.imshow("nearest neighbor", test)  # 近邻插值缩放后
cv2.imshow("image", img)  # 原图
cv2.waitkey(0)

运行结果：

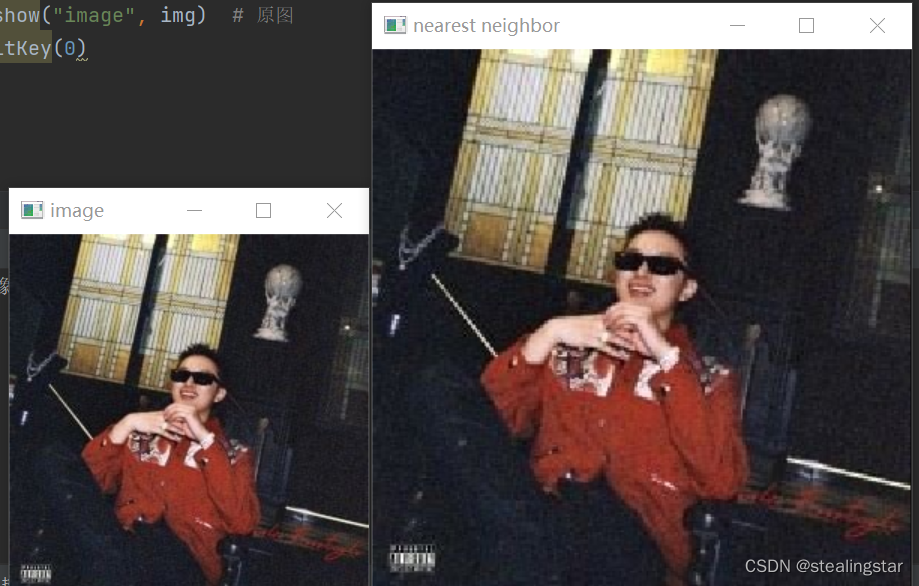
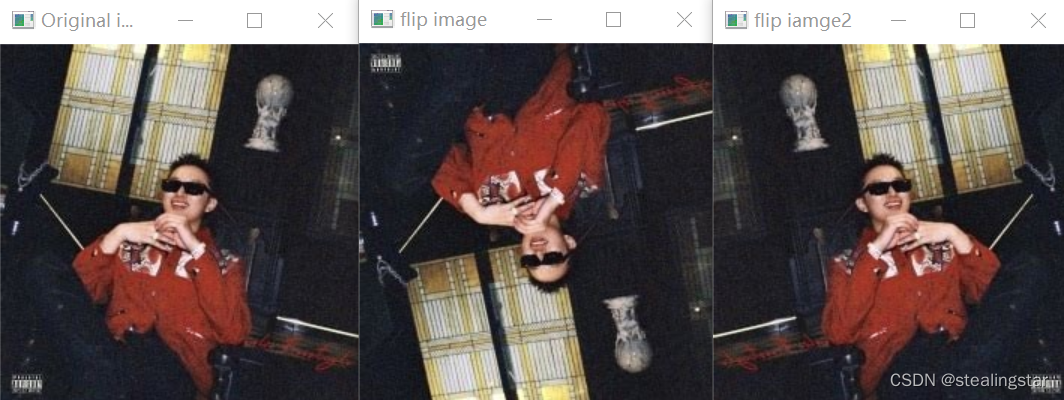
（4）镜像

opencv的函数flip()可以实现图像沿x轴翻转、沿y轴翻转、同时沿x轴和y轴翻转，从而实现图像的水平镜像和垂直镜像。

函数()的c++原型如下：

void cv::flip(inputarray src,

outputarray dst,

int flipcode )

如果flipcode的值大于0，表示绕y轴翻转，对应于实现图像的水平镜像；
如果flipcode的值等于0，表示绕x轴翻转，对应于实现图像的垂直镜像；
如果flipcode的值小于0，表示同时绕x轴和y轴翻转，对应于同时实现图像的垂直镜像和水平镜像

运行结果：

四、实验心得

本次图像处理实验主要是对图像进行了灰度值的变化，以及平移、镜像、放大、旋转等操作。我使用的是python，python中的opencv库中包含许多丰富图像处理函数，我们可以方便的直接使用这些封装好的函数，但是对于我们学习这门课程的主要意义不仅仅是会进行图像处理，还要明白图像处理的原理，以及函数实现的过程。这就要求我们可以不使用库函数的情况下，自己编写相应的插值方法来实现图像的放大缩小等操作。总而言之，图像处理对我们生活方方面面影响巨大，我们学习这门课程要懂得图像处理原理，并运用于实践当中。