文章目录
前言
本文是我学习pomdp相关的笔记,由于个人能力所限,可能有所纰漏,还请批评指正。初学者,希望和大家共同学习.
markov property
markov property或者markov assumption:
未来状态的概率分布只与当前状态有关,而与过去状态无关。
p s s ′ \boldsymbol{p}_{ss^{\prime}} pss′为从状态 s s s转移到状态 s ′ s' s′的概率,又称一步状态转移概率。 p \boldsymbol{p} p为一步状态转移矩阵。
p [ s t + 1 ∣ s t ] = p [ s t + 1 ∣ s 1 , … , s t ] p s s ′ = p [ s t + 1 = s ′ ∣ s t = s ] p = [ p 11 p 12 … p 1 n p 21 p 22 … p 2 n … … p n 1 p n 2 … p n n ] \begin{gathered} p[s_{t+1}|s_t]=p[s_{t+1}|s_1,\ldots,s_t] \\ \boldsymbol{p}_{ss^{\prime}}=p[s_{t+1}=s^{\prime}|s_{t}=s] \\ \boldsymbol{p}=\begin{bmatrix}p_{11}&p_{12}&\ldots&p_{1n}\\p_{21}&p_{22}&\ldots&p_{2n}\\\ldots\\\ldots\\p_{n1}&p_{n2}&\ldots&p_{nn}\end{bmatrix} \end{gathered} p[st+1∣st]=p[st+1∣s1,…,st]pss′=p[st+1=s′∣st=s]p= p11p21……pn1p12p22pn2………p1np2npnn
矩阵有以下性质:
- 非负性性质, p i j ≥ 0 p_{ij}\geq0 pij≥0
- 行元素和为1, ∑ p i j = 1 , i = 1 , 2 , . . . , n \sum p_{ij}=1,i=1,2,...,n ∑pij=1,i=1,2,...,n
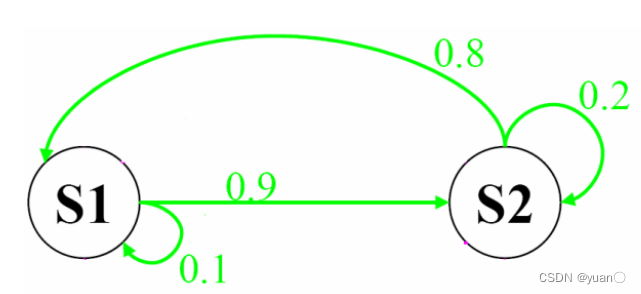
以上图为例,
s
1
s_1
s1转移到自身和
s
2
s2
s2的概率分别为0.1,0.9;
s
2
s_2
s2转移到自身和
s
1
s1
s1的概率分别为0.2,0.8。状态转移矩阵可表示为:
p
=
[
0.1
0.9
0.8
0.2
]
\boldsymbol{p}=\begin{bmatrix}0.1&0.9\\0.8&0.2\end{bmatrix}
p=[0.10.80.90.2]
markov chain
时间和状态都是离散的马尔科夫过程称为马尔科夫链markov chain.markov chain可由二元组 ( s , p ) (s, p) (s,p)描述。状态转移概率不随时间发生变化。
hidden markov model
隐马尔可夫模型(hidden markov model, hmm)是一种统计模型,它用于描述一个含有隐含未知参数的马尔可夫过程。通俗地说,就是在一个不可见的马尔可夫链的基础上,系统会根据内部状态的转移次数发生事件,从而观察到系统的输出。它在语音识别、自然语言处理、生物信息学等领域得到了广泛应用。
在hmm中,假设只有观测到的状态是可见的,而模型的内部状态是不可见的。每个状态对应于一个观测值,然后通过观测值的分布和状态转移的概率来定义模型的参数。具体来说,hmm由以下几部分组成:
- 状态序列:用s表示,其中,每个状态s属于状态集合 s = s 1 , s 2 , . . . , s n s={s_1, s_2, ..., s_n} s=s1,s2,...,sn。
- 观测序列:用o表示,其中,每个观测 o o o属于观测集合 o = o 1 , o 2 , . . . , o m o={o_1, o_2, ..., o_m} o=o1,o2,...,om。
- 状态转移概率:用 p i j p_{ij} pij表示,表示从状态 s i s_i si转移到状态 s j s_j sj的概率,其中 p = p i j p={p_{ij}} p=pij是一个 n × n n\times n n×n的矩阵,且对于所有的 i i i, ∑ j = 1 n p i j = 1 \sum_{j=1}^{n}p_{ij}=1 ∑j=1npij=1。
- 观测概率:用 b i ( o ) b_{i}(o) bi(o)表示,表示在状态 s i s_i si时观测到 o o o的概率,其中 b = b i ( o ) b={b_i(o)} b=bi(o)是一个 n × m n\times m n×m的矩阵,且对于所有的 i i i, ∑ o = 1 m b i ( o ) = 1 \sum_{o=1}^{m}b_{i}(o)=1 ∑o=1mbi(o)=1。
- 初始状态概率:用
π
i
{\pi_{i}}
πi表示,表示初始状态为
s
i
s_i
si的概率,其中
π
=
π
i
\pi={\pi_{i}}
π=πi是一个长度为
n
n
n的向量,且对于所有的
i
i
i,
∑
i
=
1
n
π
i
=
1
\sum_{i=1}^{n}\pi_{i}=1
∑i=1nπi=1。

markov decision process
mdp(markov decision process)是用于描述智能体与环境交互的数学模型。mdp 可以表示为五元组 ( s , a , p , r , γ ) (s, a, p, r, \gamma) (s,a,p,r,γ):
- s s s:状态集合, s = { s 1 , s 2 , . . . , s n } s=\{s_1, s_2, ..., s_n\} s={s1,s2,...,sn},包含了车道、环境、世界模型等信息。
- a a a:动作集合, a = { a 1 , a 2 , . . . , a m } a=\{a_1, a_2, ..., a_m\} a={a1,a2,...,am},车辆的决策空间,包含换道、跟随、超车等等。
- p ( s ′ ∣ s , a ) p(s'|s, a) p(s′∣s,a):状态转移概率,表示在当前状态 s s s 下,采取动作 a a a 后转移到状态 s ′ s' s′ 的概率, s ′ ∈ s s'\in s s′∈s, s , s ′ ∈ s s, s'\in s s,s′∈s, a ∈ a a\in a a∈a。
- r ( s , a , s ′ ) r(s, a, s') r(s,a,s′):即时奖励函数,表示在当前状态 s s s 下,采取动作 a a a 后转移到状态 s ′ s' s′ 所获得的即时奖励, s , s ′ ∈ s s, s'\in s s,s′∈s, a ∈ a a\in a a∈a。
- γ ∈ ( 0 , 1 ) γ\in(0,1) γ∈(0,1):折扣因子,表示当前奖励和未来奖励的权重比例。
mdp 将智能体的行动转化为对状态的选择,使得智能体可以基于经验策略不断学习并优化其决策。因此,mdp 在强化学习等领域广泛应用。
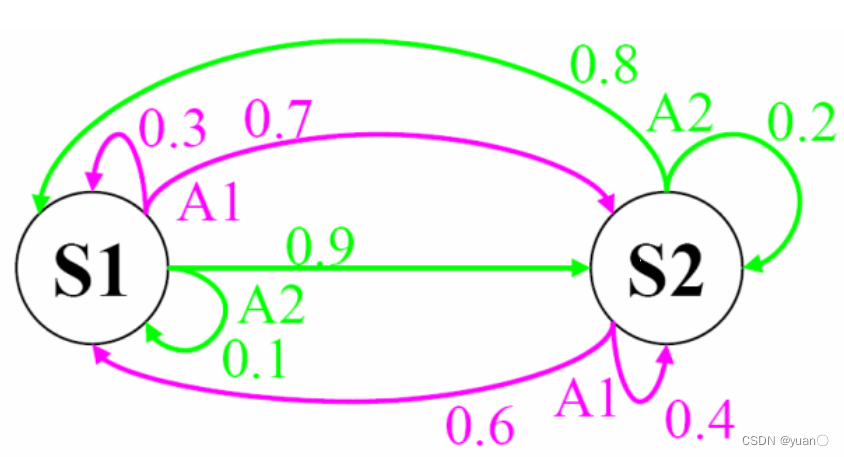
自动驾驶车辆的决策问题本质上是寻找到一个最优的策略,对于当前状态
s
s
s,通过一定的动作
a
a
a,使之达到目标状态。因此可以通过一个目标函数去最大化总的奖励:
∑
t
=
0
∞
γ
t
r
(
s
t
+
1
∣
s
t
)
\sum_{t=0}^\infty\gamma^tr(s_{t+1}|s_t)
t=0∑∞γtr(st+1∣st)动作
a
a
a可以用policy
π
\pi
π去定义:
a
=
π
(
s
)
a=\pi(s)
a=π(s),policy则是我们所求的mdp的解。
问题的解可以通过动态规划的方法进行求解,通过迭代求解最大的奖励,最后回溯得到解。假设状态转移概率矩阵
p
p
p和奖励函数
r
r
r已知,通过对以下过程的不断迭代可以得到最优解:
π
(
s
t
)
←
a
r
g
m
a
x
{
∑
s
t
+
1
p
(
s
t
+
1
∣
s
t
)
(
r
(
s
t
+
1
∣
s
t
)
+
γ
v
(
s
t
+
1
)
)
}
v
(
s
t
)
←
∑
s
t
+
1
p
π
(
s
t
)
(
s
t
+
1
∣
s
t
)
(
r
π
(
s
t
)
(
s
t
+
1
∣
s
t
)
+
γ
v
(
s
t
+
1
)
)
\begin{aligned}\pi(s_t)&\leftarrow\mathrm{argmax}\left\{\sum_{s_t+1}p(s_{t+1}|s_t)\left(r(s_{t+1}|s_t)+\gamma v(s_{t+1})\right)\right\}\\v(s_t)&\leftarrow\sum_{s_{t+1}}p_{\pi(s_t)}(s_{t+1}|s_t)(r_{\pi(s_t)}(s_{t+1}|s_t)+\gamma v(s_{t+1}))\end{aligned}
π(st)v(st)←argmax{st+1∑p(st+1∣st)(r(st+1∣st)+γv(st+1))}←st+1∑pπ(st)(st+1∣st)(rπ(st)(st+1∣st)+γv(st+1))
v ( s t ) v(s_t) v(st)为价值函数(value function),表示奖励中的累计折扣。求解过程就是在 s t s_t st和 s t + 1 s_{t+1} st+1之间不断迭代直到收敛。
对于动态规划迭代求解的过程,这篇文章简洁地揭示了相关原理(value iteration algorithm):brief introduction to the value iteration algorithm.
mdp比较重要的一点就是如何设计奖励函数,通常需要考虑以下因素:
- 抵达目标点同时不偏离路径;
- 安全性;
- 舒适性。
除此之外,状态空间、状态转移矩阵等等的设计都是十分重要的。
partially observable markov decision process
partially observable markov decision process (pomdp) 是一个基于马尔可夫决策过程 (mdp) 的扩展模型,其状态不完全可观测。pomdp 可以表示为一个七元组 ( s , a , p , r , z , o , γ ) (s, a, p, r, z, o,γ) (s,a,p,r,z,o,γ),其中:
- s s s:状态集合, s = { s 1 , s 2 , . . . , s n } s=\{s_1, s_2, ..., s_n\} s={s1,s2,...,sn},包含了车道、环境、世界模型等信息。
- a a a:动作集合, a = { a 1 , a 2 , . . . , a m } a=\{a_1, a_2, ..., a_m\} a={a1,a2,...,am},车辆的决策空间,包含换道、跟随、超车等等。
- p ( s ′ ∣ s , a ) p(s'|s, a) p(s′∣s,a):状态转移概率,表示在当前状态 s s s 下,采取动作 a a a 后转移到状态 s ′ s' s′ 的概率, s ′ ∈ s s'\in s s′∈s, s , s ′ ∈ s s, s'\in s s,s′∈s, a ∈ a a\in a a∈a。
- r ( s , a , s ′ ) r(s, a, s') r(s,a,s′):即时奖励函数,表示在当前状态 s s s 下,采取动作 a a a 后转移到状态 s ′ s' s′ 所获得的即时奖励, s , s ′ ∈ s s, s'\in s s,s′∈s, a ∈ a a\in a a∈a。
- γ ∈ ( 0 , 1 ) γ\in(0,1) γ∈(0,1):折扣因子,表示当前奖励和未来奖励的权重比例。
- z z z 是观测集合, z = { z 1 , z 2 , . . . , z n } z=\{z_1, z_2, ..., z_n\} z={z1,z2,...,zn};
- o ( z ∣ s ′ , a ) o(z|s', a) o(z∣s′,a) 是观测函数 o : s × a × z → [ 0 , 1 ] o: s \times a \times z \rightarrow [0, 1] o:s×a×z→[0,1],定义了在执行一个动作 a ∈ a a \in a a∈a 后,在一个状态 s ∈ s s \in s s∈s 产生一个观测 z ∈ z z \in z z∈z 的概率。
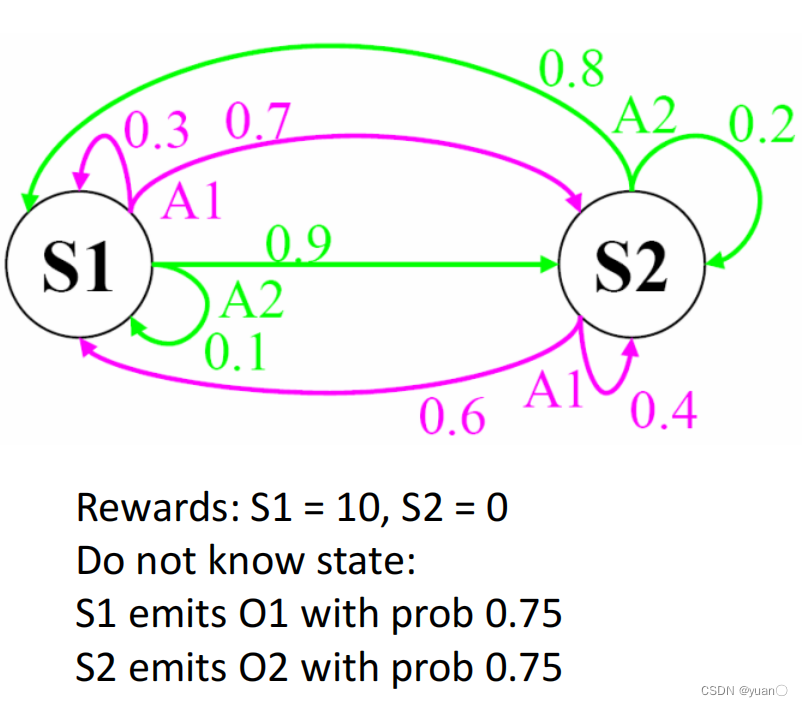
在pomdp中,将一组观测值(observation)添加到模型中。我们不能直接观测到当前的状态,而是通过整个模型的全域和状态给予的观测值去估计当前的状态是什么。观测值通常是一个概率,因此需要建立相应的观测模型。
background on solving pomdps
这部分内容参考了https://cs.brown.edu/research/ai/pomdp/tutorial/pomdp-solving.html。
对于co-mdp(完全可观的mdp)问题,我们需要找到状态state与动作action的映射关系;而对于pomdp问题,我们需要找到基于状态的概率分布与动作之间的映射关系。在接下来的部分,我们用belief state(信念状态)来代替基于状态的概率分布(probability distribution over states);用belief space(信念空间)来代替概率空间probability space (the set of all possible probability distributions)。
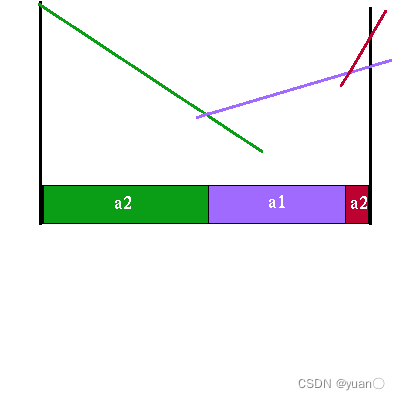
接下来这幅图将会描述信念空间的概念。为了简化问题,我们采用2个状态的pomdp问题进行阐述。从前面的内容中可知,信念状态代表概率分布,所有的概率之和应该为1.因此在2 state pomdp问题中,若一个状态的概率为 p p p,这另一个状态概率为 1 − p 1-p 1−p.于是,整个信念空间可以用一个线段进行描述。线段宽度可忽略。

如图所示,若信念状态非常靠近最左边时,意味着处于状态 s 2 s_2 s2的概率为1,反之这是处于状态 s 1 s_1 s1的概率为1。值得注意的是,将2 state推广到高维空间时亦成立。
接着,若假设我们从一个指定的信念状态 b b b开始,然后采取动作 a 1 a_1 a1并且收到观测值 z 1 z_1 z1,于是下一个信念状态就可以完全确定了。事实上,若我们假定有有限个的动作actions以及有限个数量的观测值observations,给定一个信念状态,就可以确定接下来的信念状态。
下图显示了上述的过程:两个state(
s
1
,
s
2
s_1,s_2
s1,s2),两个actions(
a
1
,
a
2
a_1,a_2
a1,a2)以及三个observations(
z
1
,
z
2
,
z
3
z_1,z_2,z_3
z1,z2,z3),黑色竖线段为起始的信念状态。
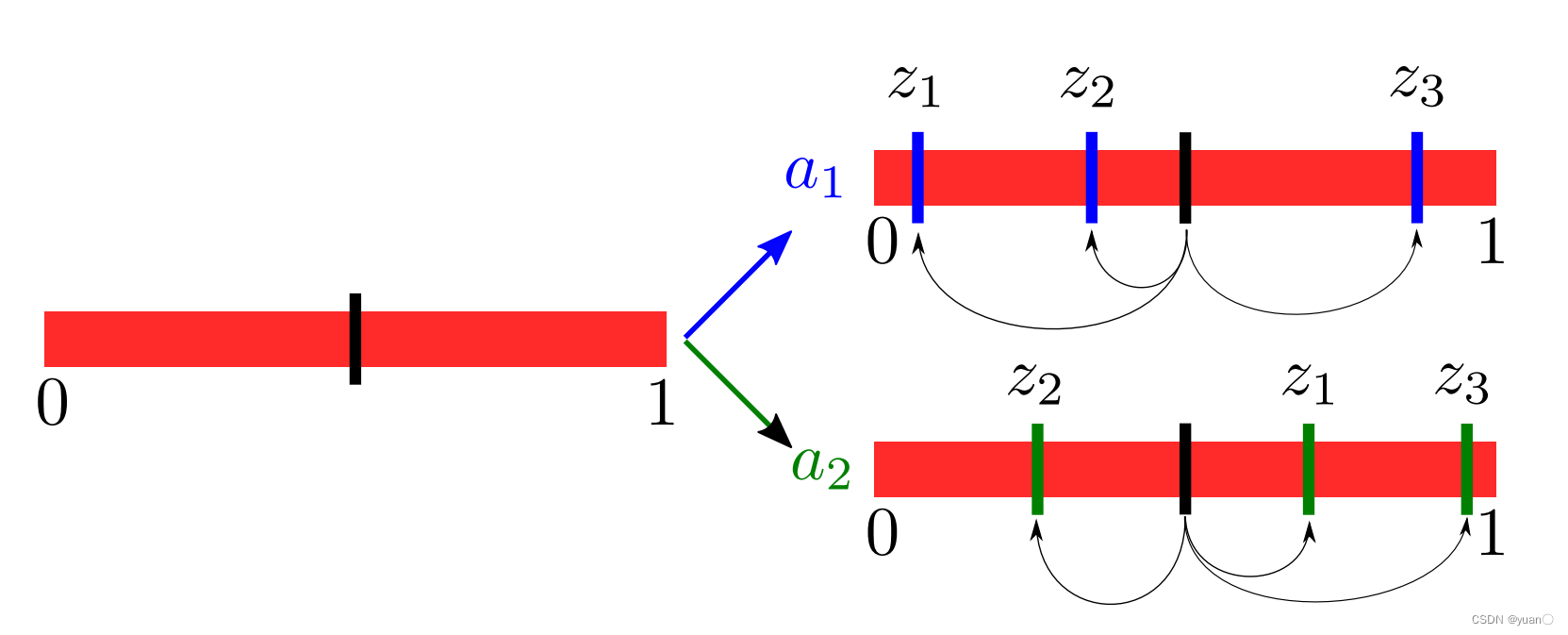
上图显示了所有可能的信念状态。总结一下:对于一个起始的信念状态,若产生一个动作并且得到相应的观测值,就可以确定下一个信念状态。不过对于一个pomdp问题中,在产生一个action之前,每一个最终的信念状态都会对应相应的概率,而这样的信念状态(包括相应的observations)有很多,但是对于一个action,下一步的信念状态所对应的概率之和应该为1.
显然,上述的过程符合markov property,下一步的信念状态取决于上一步信念状态(以及action和observations)。事实上,我们可以将离散的pomdp问题转化为连续空间的co-mdp问题,其中连续空间是信念空间。也就意味着我们可以利用value iteration (vi) algorithm进行求解。但是这个算法还需要被进一步完善。
在一些教程里,将其描述为belief-mdp。
mdp的可以很好地利用value iteration进行求解,因为其状态是离散的,每一个状态的价值函数也是离散的。但是pomdp问题则不一样,因为状态(信念状态)是连续的,就需要合理的一个价值函数进行描述。下图是价值函数的一个示例:
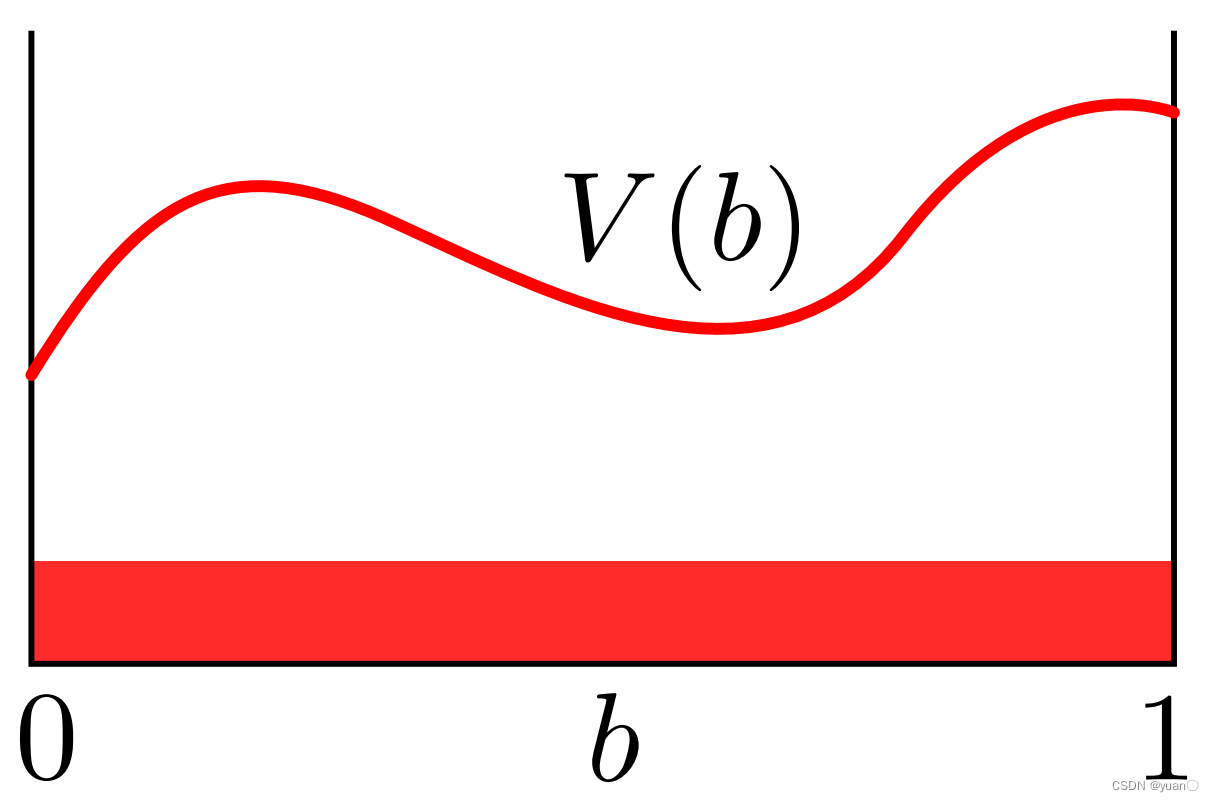
pomdp公式对于上述问题施加了相关约束。核心点就是:对于每一个视野长度horizon length,价值函数是分段线性且凸的piecewise linear and convex (pwlc) 。这就意味着对于每一个值迭代过程,我们只需要找到有限个的线段去构造价值函数。
下图是相应的例子,重合部分的线段取最大值。
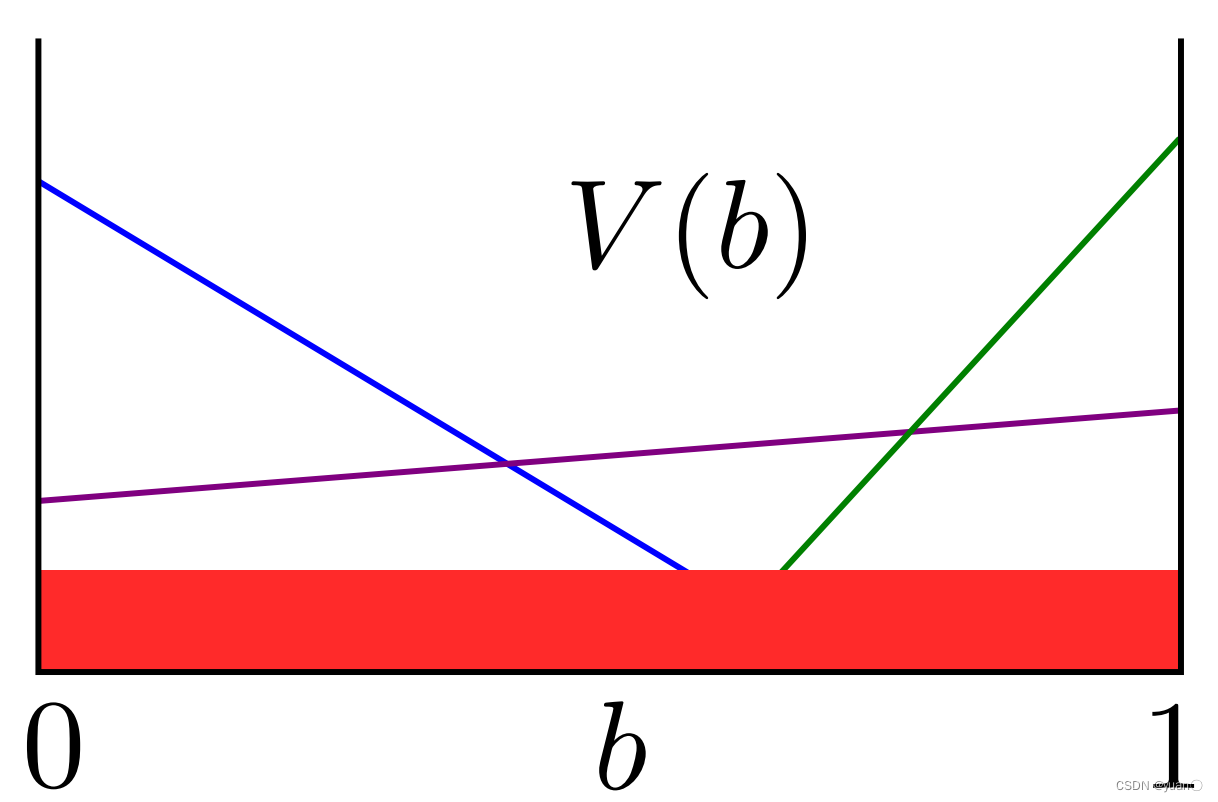
如果我们将超平面表示为一个向量(即方程的系数,又称为alpha vector),并将每个信念状态表示为一个向量(每个状态的概率),那么信念状态的价、值就是两个向量的点积( α ⋅ b \alpha \cdot b α⋅b)。
下面是另一种方式,将信念空间分段,两者其实是等效的:
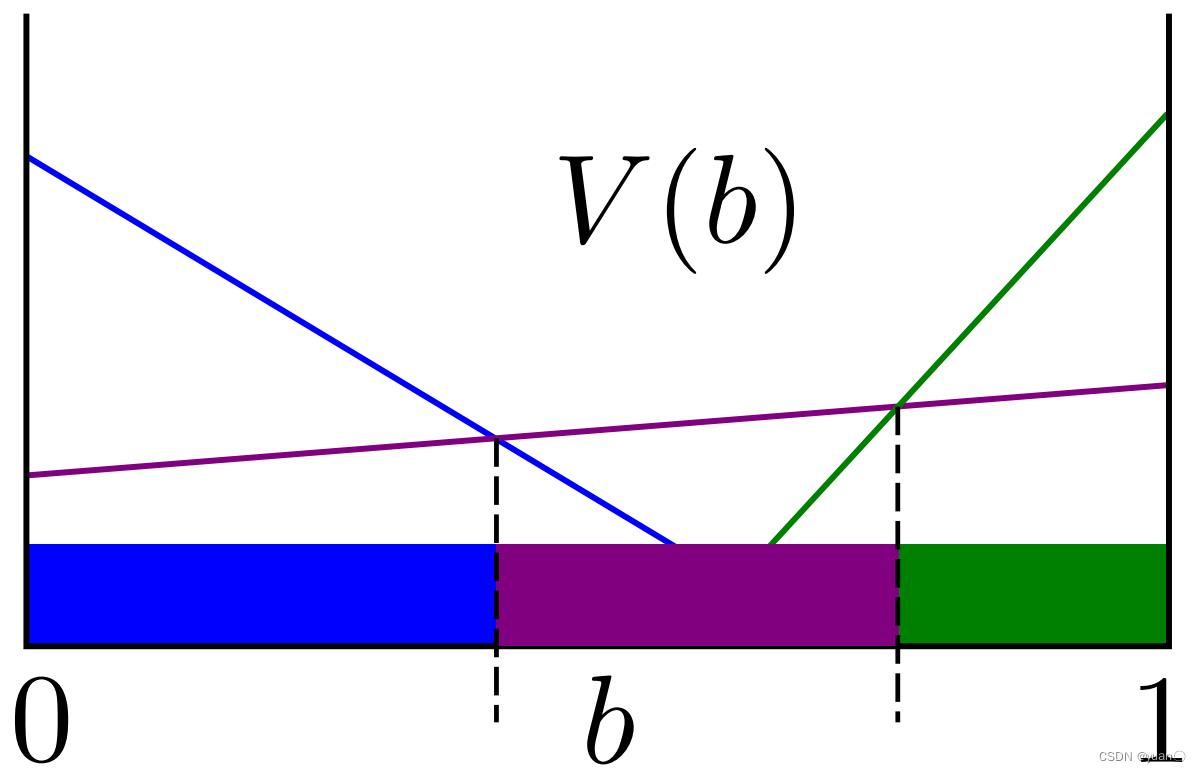
总结一下:给定一组合向量表示某一时间窗口(或称时间步长)'h’的价值函数,我们通常需要推导出时间窗口 ‘h+1’ 的价值函数的向量集合。
但是,连续状态空间的确会带来进一步的问题。在离散状态空间中的每次值迭代中,我们可以通过遍历所有可能的下一个状态来找到一个状态的新值。然而,对于连续状态 co-mdps,我们无法枚举所有可能的状态,因为它们是"无限"的。
接下来将会介绍一系列方法用以解决上述问题。
pomdp value iteration example
接下来是一个horizon length为3的例子。依旧是两个state( s 1 , s 2 s_1,s_2 s1,s2),两个actions( a 1 , a 2 a_1,a_2 a1,a2)以及三个observations( z 1 , z 2 , z 3 z_1,z_2,z_3 z1,z2,z3)
horizon 1 value function
对于horizon=1的情况,我们只关心即刻的奖励,因此价值函数就变成了即刻奖励的函数,而不再考虑未来奖励的影响(就是不用考虑折扣因子 γ \gamma γ的影响)。
对于此问题,我们有两个state和两个action,因此我们有四种行为和状态的组合,每种组合有不同的价值:
r
(
s
1
,
a
1
)
,
r
(
s
2
,
a
1
)
,
r
(
s
1
,
a
2
)
,
r
(
s
2
,
a
2
)
r(s_1,a_1),r(s_2,a_1),r(s_1,a_2),r(s_2,a_2)
r(s1,a1),r(s2,a1),r(s1,a2),r(s2,a2)
这些价值是离散的(基于离散state的pomdp),但是若是在一个特定的信念状态去执行一个特定的action,这个值就变得容易获得。我们只需使用信念状态的概率分布作为每个state价值的权重。
用一个简单例子来进一步理解:若执行action a 1 a_1 a1时,价值为 r ( s 1 , a 1 ) = 1 , r ( s 2 , a 1 ) = 0 r(s_1,a_1)=1,r(s_2,a_1)=0 r(s1,a1)=1,r(s2,a1)=0,执行action a 2 a_2 a2时,价值为 r ( s 1 , a 2 ) = 0 , r ( s 2 , a 2 ) = 1.5 r(s_1,a_2)=0,r(s_2,a_2)=1.5 r(s1,a2)=0,r(s2,a2)=1.5。若当前的信念状态为 [ 0.25 , 0.75 ] [0.25,0.75] [0.25,0.75](意味着我们“相信”当前有75%的可能在 s 2 s_2 s2,有25%的可能在 s 1 s_1 s1),则可得到执行 a 1 a_1 a1的价值为: 0.25 × 1 + 0.75 × 0 = 0.25 0.25 \times 1 + 0.75 \times 0 = 0.25 0.25×1+0.75×0=0.25,执行 a 2 a_2 a2的价值为: 0.25 × 0 + 0.75 × 1.5 = 1.125 0.25 \times 0 + 0.75 \times 1.5 = 1.125 0.25×0+0.75×1.5=1.125。我们可以用下图在信念空间上显示这些值。
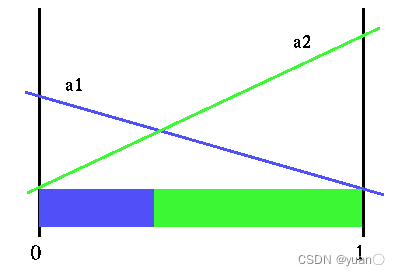
可以看到,每一个action对应的即时奖励都指定了一段在信念空间上的线性函数。基于特定的信念状态,我们会去选择能带来更高收益的动作。上图中对于绿色部分的信念空间,显然选择 a 2 a_2 a2会带来更高的收益,而蓝色部分的信念空间,选择 a 1 a_1 a1会带来更高的收益。
horizon 2 value function
接下来介绍horizon 2 value function的情况。
我们的目的是找到在每个信念状态中,仅使用两种行动的最佳策略。这个问题比较复杂,我们将问题拆解,去依次回答如下3个问题:
- 如何在给定一个action和observation的情况下计算单个信念状态的价值。
- 如何在只给定action的情况下计算一个信念状态的价值。
- 如何计算一个信念状态的价值.
v(b) given a and z
首先从第一个问题开始:给定一个特定的信念状态 b b b,如何计算在执行action a 1 a_1 a1并收到观测值observation z 1 z_1 z1的情况下的价值。
在horizon=2的情况下,当前每个信念状态的价值就是即时行动的价值加上下一个行动的价值。因为我们固定了即时行动的action,所以总的流程其实类似于horizon=1的情况。
来看下图的例子:
左边是即时奖励的函数,右边是horizon=1时的价值函数。
a
2
a_2
a2的即时奖励函数是虚线,我们不必去考虑它(因为我们已经给定了action
a
1
a_1
a1)。

我们定义 t t t是在给定 a 1 , z 1 a_1,z_1 a1,z1下,从信念状态 b b b转移到 b ′ b' b′的函数。从 b ′ b' b′的角度去看,很容易决定选择哪一个action能够带来更高的收益。上图的 b ′ b' b′落在绿色的区域,意味着对于horizon=2的情况,若我们首先选择 a 1 a_1 a1,且观测到了 z 1 z_1 z1,那么接下来选择 a 2 a_2 a2会给我们带来更大的收益。显然,我们知道所有需要计算价值的变量,知道了即时奖励的值,知道转移到 b ′ b' b′后的最佳的价值,只需要将两者相加,就可以求得在给定 a 1 , z 1 a_1,z_1 a1,z1时, b b b状态下的价值。
我们可以通过重复上一节的步骤计算任意的一个信念状态的价值(即刻回报+转换后的价值)。接下来我们希望找到所有的信念状态的价值(横轴上[0,1]中每一个点的价值)。
horizon=1时的价值函数是基于转移后的信念状态 b ′ b' b′的函数, b ′ b' b′则是在给定 a 1 , z 1 a_1,z_1 a1,z1下基于初始信念状态 b b b的转移函数( b ′ = τ ( b , a 1 , z 1 ) b'=\tau(b,a_1,z_1) b′=τ(b,a1,z1))。因此,我们可以根据horizon=1的价值函数,在整个信念空间上构造一个函数,这个函数内置了转移函数 b ′ = τ ( b , a 1 , z 1 ) b'=\tau(b,a_1,z_1) b′=τ(b,a1,z1)。
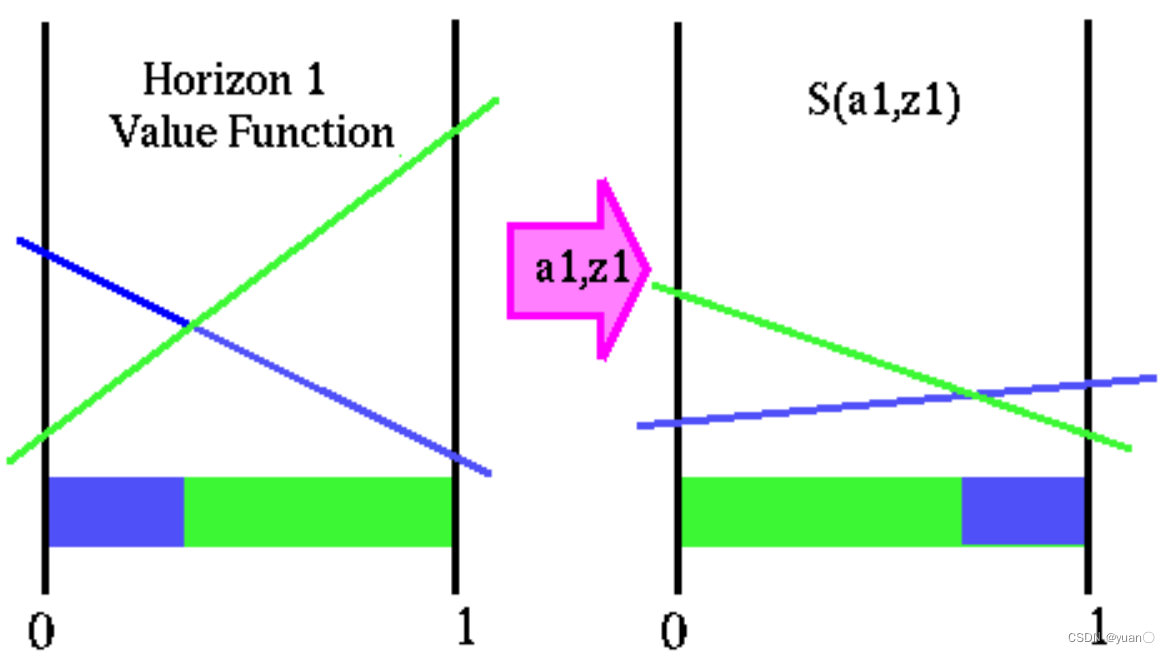
接着,我们可以使用 s ( a i , z j ) s(a_i,z_j) s(ai,zj)去代表上述的函数(transformed value function)。现在,如果我们要找到一个给定 ( a i , z j ) (a_i,z_j) (ai,zj)的信念状态,只需要将 s ( a i , z j ) s(a_i,z_j) s(ai,zj)和即时奖励 r ( s i , a i ) r(s_i,a_i) r(si,ai)相加即可。
v(b) given a
接着上面的问题,对于给定的
(
a
i
,
z
j
)
(a_i,z_j)
(ai,zj),我们可以通过上述的方法知道一个信念状态
b
b
b的价值。然而,通常情况下,observation
z
z
z是不可知的,我们不能保证就能观测到给定的
z
j
z_j
zj值。因此,我们给出下面的例子,进一步对问题进行解释:
如图所示, b b b在给定动作 a 1 a_1 a1的情况下,可能会出现三种观测值 z 1 , z 2 , z 3 z_1,z_2,z_3 z1,z2,z3,并导致三种可能的结果。
解决这个问题很简单:如果我们知道给定观测值
z
j
z_j
zj后的信念状态的结果,那么即便我们不知道观测值,我们也可以计算信念状态的价值:用每个观察结果
z
j
z_j
zj出现的概率进行加权得即可。
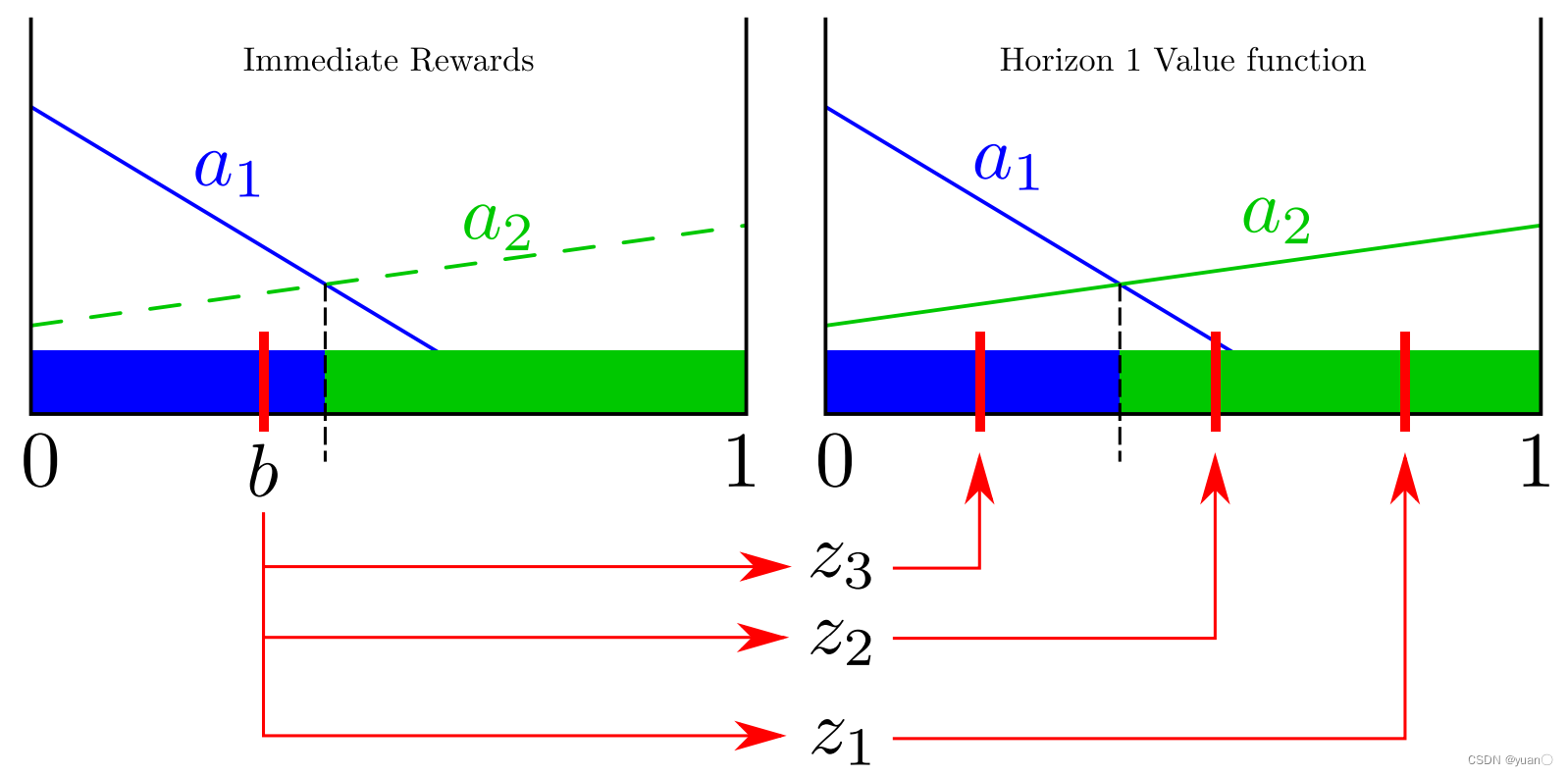
在这个例子中(有三个可能的observation),每一个 z i z_i zi都有对应的 s s s函数。很明显可以得到一个结论:下一步要采取的最佳行动不仅取决于最初的信念状态,还取决于我们得到的确切观测结果。
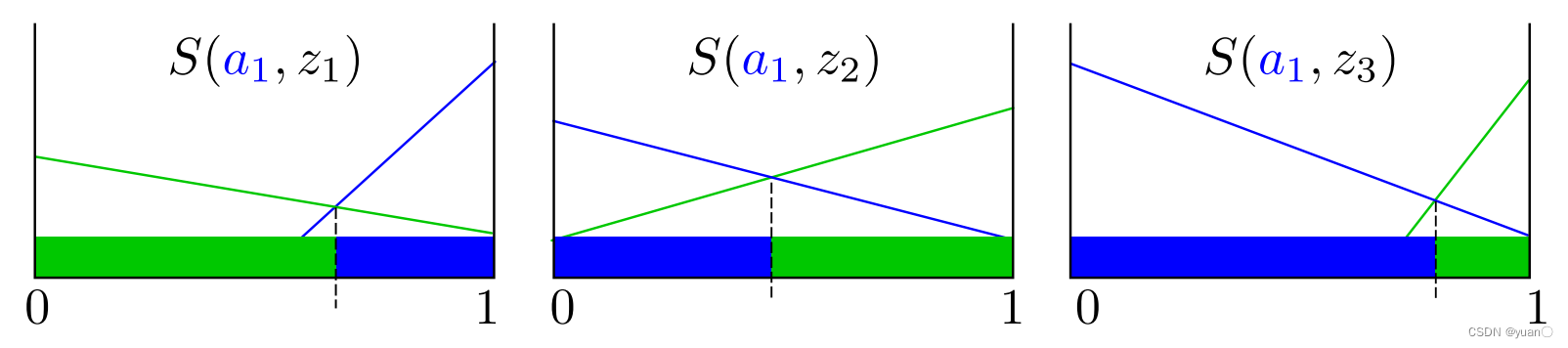
horizon=2时的价值不仅仅取决于给定的动作
a
1
a_1
a1,还取决于下一步的动作。对于给定的信念状态和观测值,我们可以查看
s
s
s函数分区,以决定下一步要做的最佳操作是什么。
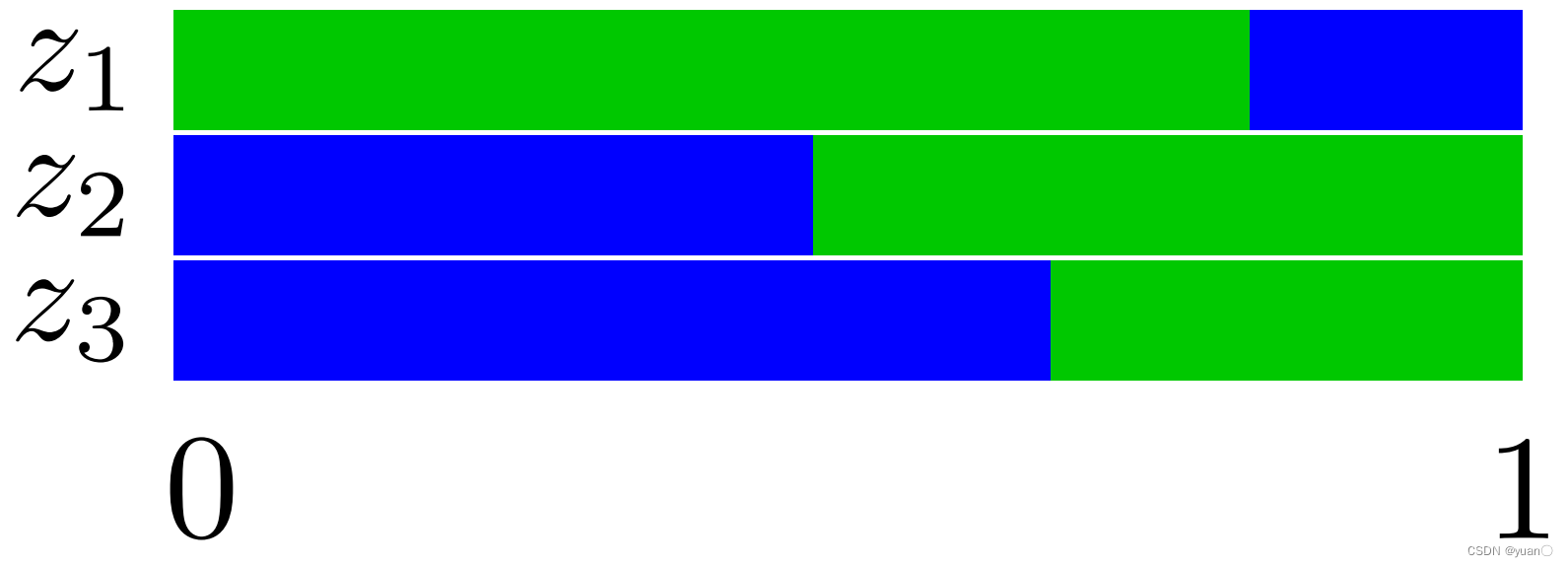
如下图所示,若给定信念状态 b b b,动作 a 1 a_1 a1,我们很容易从图中知道接下来的策略:若观测到 z 1 z_1 z1,则执行 a 2 a_2 a2;若观测到 z 2 , z 3 z_2,z_3 z2,z3,则执行 a 1 a_1 a1。对于信念空间中的每一个点,我们都可以划这么一条竖线,得到在这个信念状态下的策略:如果观察到 z i z_i zi,则选择 a j a_j aj。 下图的策略就是 ( z 1 : a 2 , z 2 : a 1 , z 3 : a 1 ) (z_1:a_2, z_2:a_1, z_3:a_1) (z1:a2,z2:a1,z3:a1)。

v(b)
但是,上述的过程只是代表了在信念状态 b b b中能够获得的最优策略,并不代表是所有信念状态 b i b_i bi的最优策略。接着来看下面的图:
下图中,上面的矩形中不同的颜色代表了对应于不同最优策略
b
b
b的范围。我们有三个观测值
z
1
,
z
2
,
z
3
z_1,z_2,z_3
z1,z2,z3,两个动作
a
1
,
a
2
a_1,a_2
a1,a2,因此我们有8种对应的策略,但并非每一种策略都是有效的(任何情况下非最优),比如图中这个例子就只有4种策略。
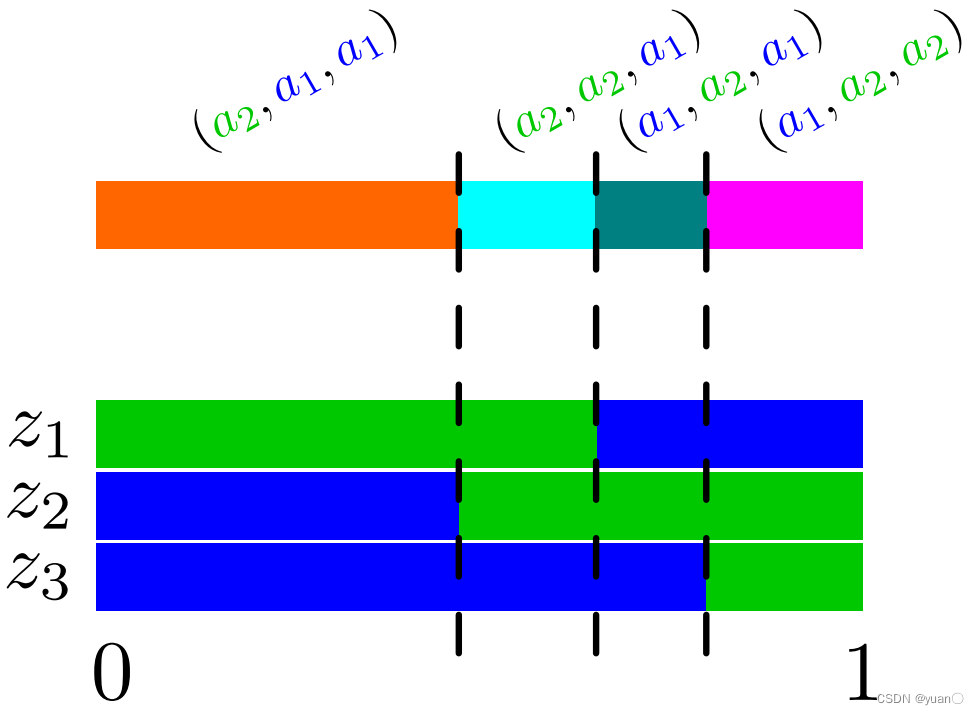
同样地,可以为这之中的四个构造相应的线段,最后会得到如下图所示的线性分段凸函数。
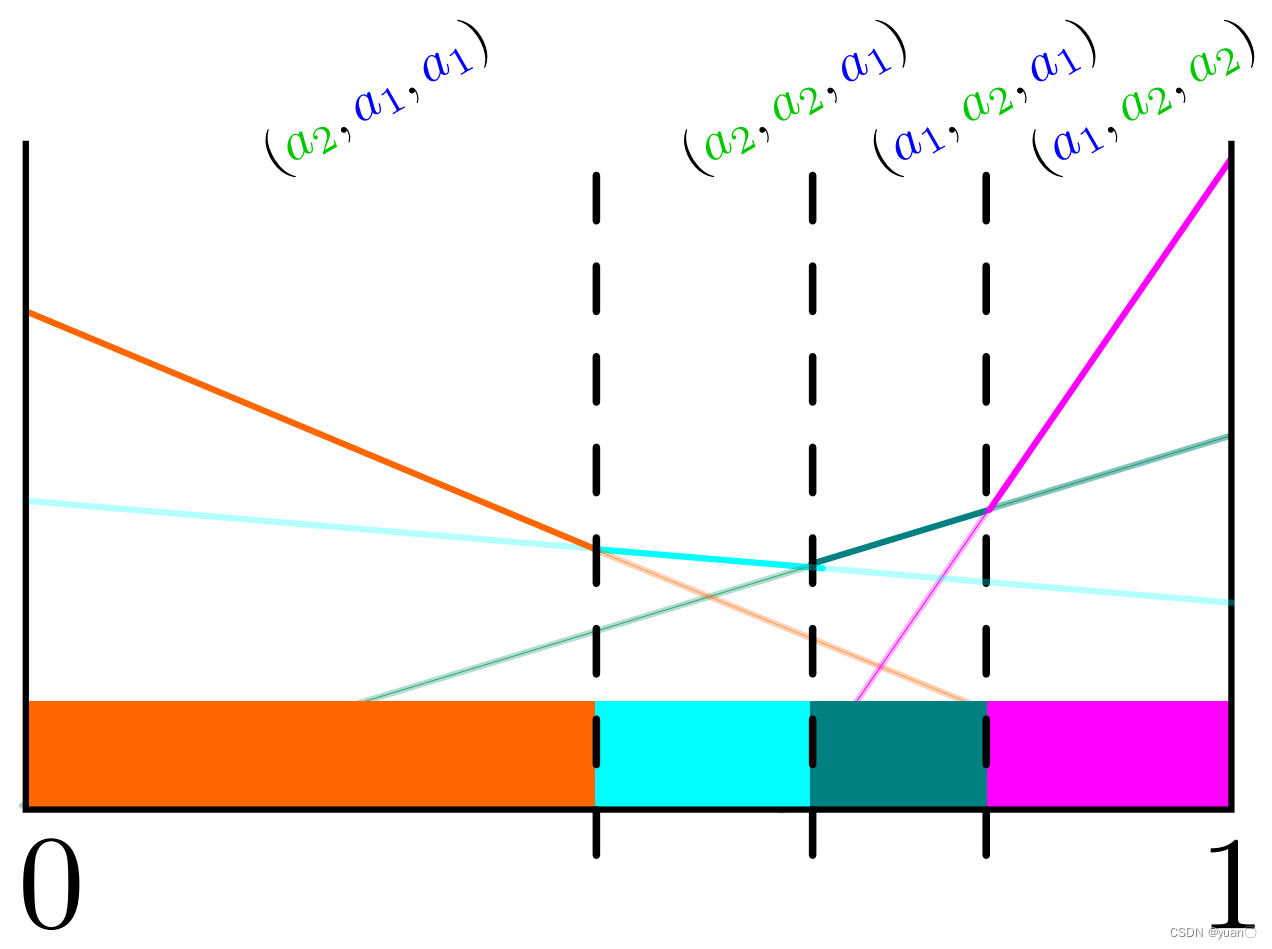
注意上图中的每一个线段代表了两个动作:action a 1 a_1 a1以及依赖于观测的另一个动作。
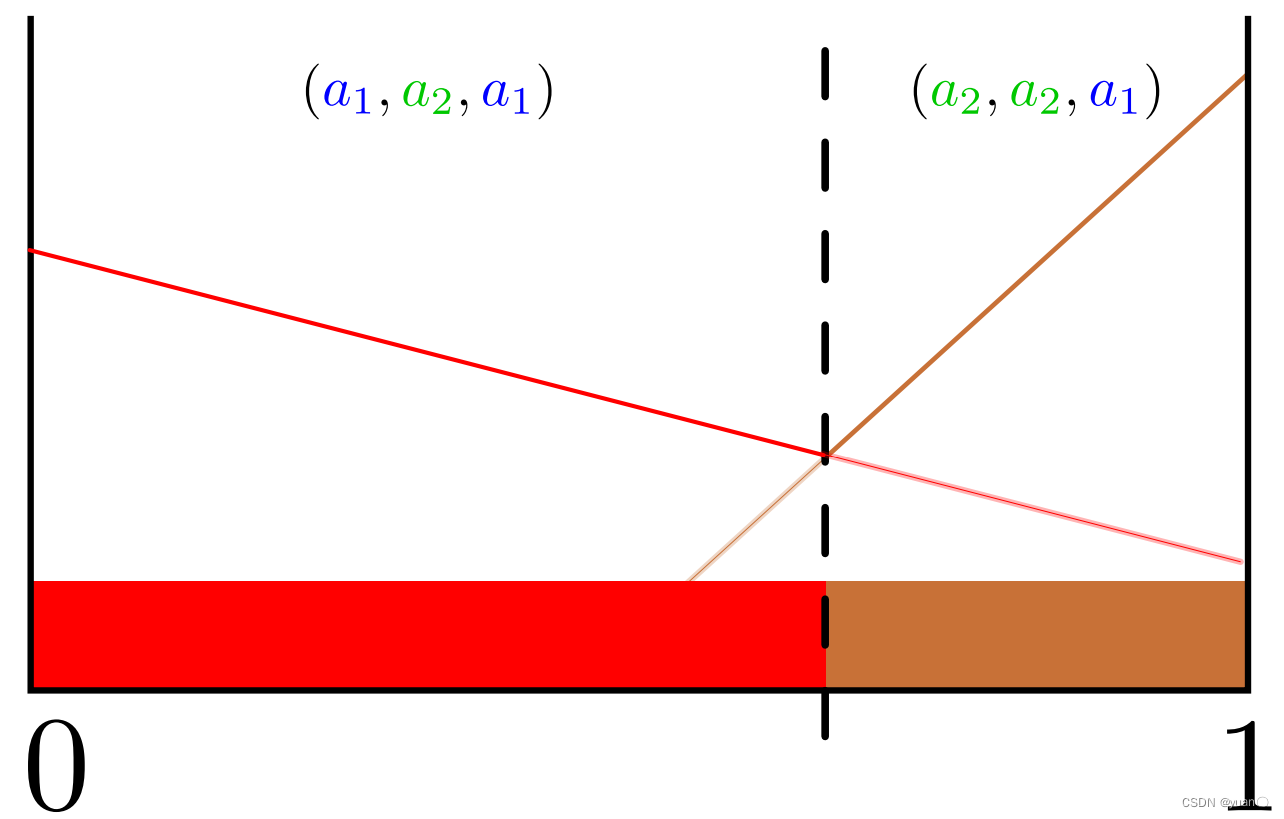
若我们的模型中只有一个动作
a
1
a_1
a1,那么上述的过程就已经结束了,我们也得到了horizon=2的价值函数。但是,我们还有其他action。如上图所示,对
a
2
a_2
a2也重复上述过程,可得到
a
2
a_2
a2的价值函数以及具有两个分区的图。
接着,我们将
a
1
a_1
a1和
a
2
a_2
a2两个价值函数进行叠加,从而去找到哪一个action能够提高更大的价值。
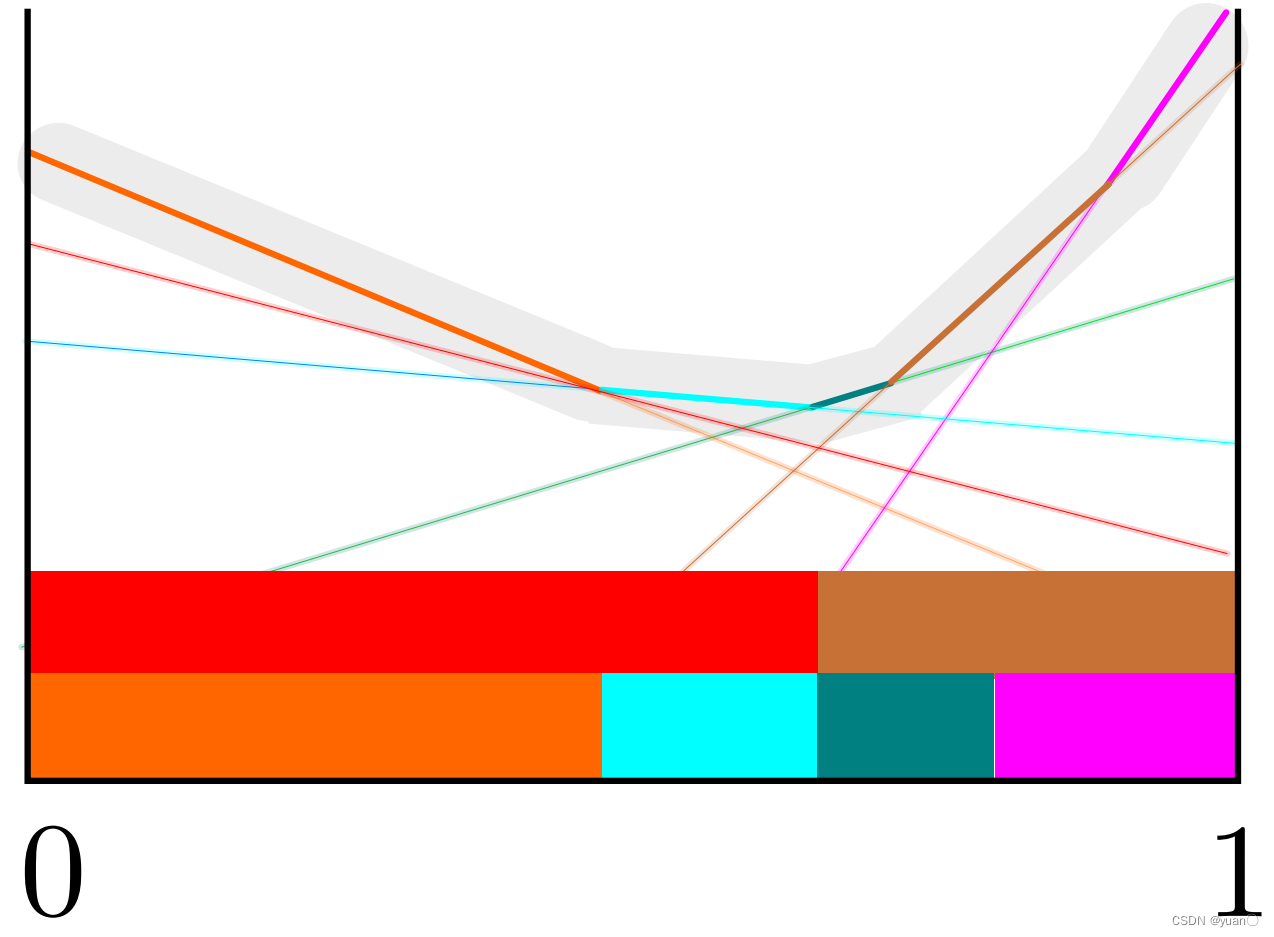
同样是构造pwlc,可以注意到有些线段对于两个动作来说都是无效的,因此被剪枝。最后得到下图所示的horizon=2时的价值函数。
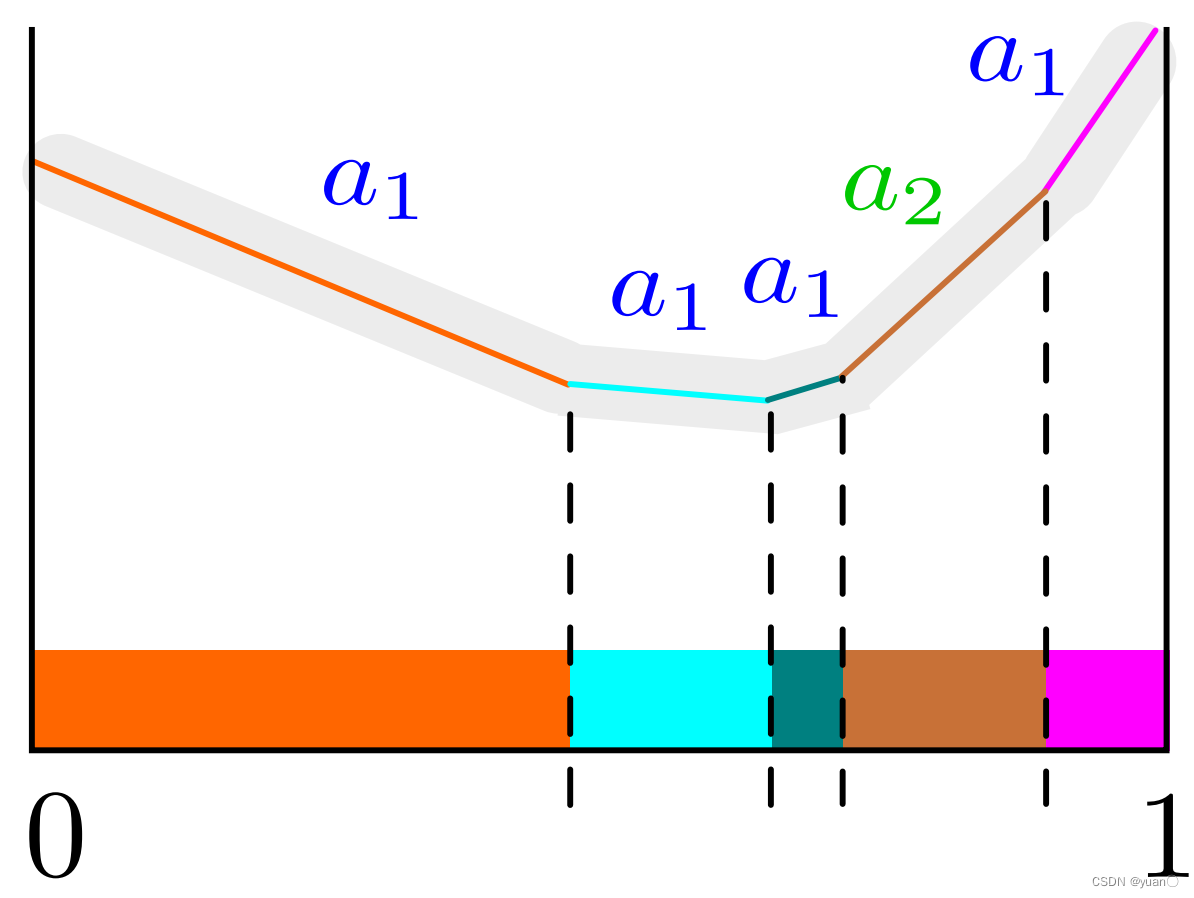
horizon 3 value function
horizon=3的情况类似于horizon=2的情况。首先对
a
1
a_1
a1构造价值函数(同样利用
s
s
s函数将horizon=2的价值函数进行转移变换)。如下图所示,有六种有效策略。
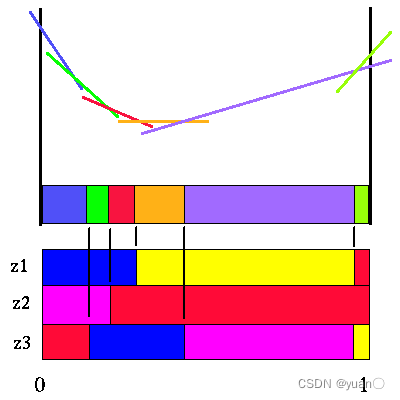
接着构造
a
2
a_2
a2的价值函数,如下图所示,有4种有效策略。
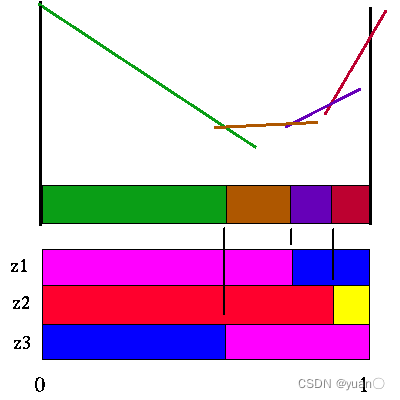
将两者叠加可得到,
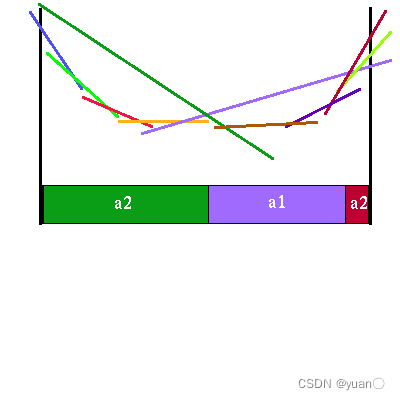
我们将两个可能的action的情况结合起来,并进行剪枝(去掉无法达到最优的策略),那么最终右下图就是horizon=3的value function了。
目前解决pomdp的方法有预测模型法。引入置信度,将问题转化为统计上的mdp进行解决。

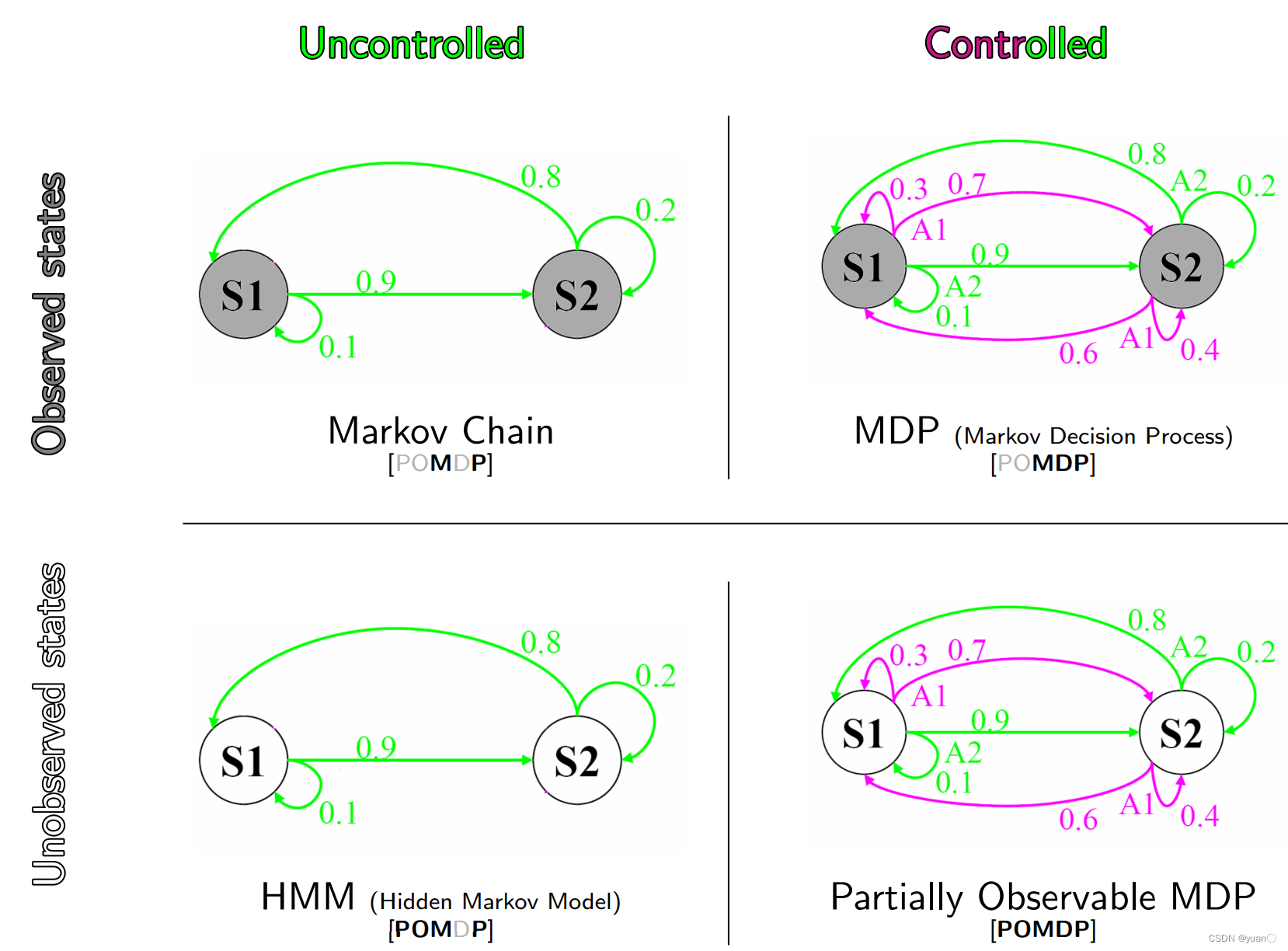
下面这张图很好地显示了四种markov模型之间的关系。
推荐阅读与参考
[1] https://cs.brown.edu/research/ai/pomdp/tutorial/(讲解mdp和pomdp,非常通俗易懂)
[2] http://cbl.eng.cam.ac.uk/pub/intranet/mlg/readinggroup/pomdp.pdf
[3] https://besjournals.onlinelibrary.wiley.com/doi/full/10.1111/2041-210x.13692
[4] [规划问题] 1 pomdp值迭代的直观理解
[5] https://www.cs.cmu.edu/~ggordon/780-fall07/lectures/pomdp_lecture.pdf





发表评论