【数据结构】建堆算法复杂度分析及top-k问题

🔥个人主页:大白的编程日记
🔥专栏:数据结构
前言
一.复杂度分析
我们都知道堆是一个完全二叉树。那他的高度h和节点数量n有什么关系呢?

那我们再来对比一下满二叉树和完全二叉树的高度h.

我们用大o渐进表示法看的话他们两个的高度h都可以认为是logn的量级
所以我们的堆的上下调整可以认为是logn,也就是高度次。
1.1向下建堆复杂度
我们先分别算出第一层到h-1层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

1.2向上建堆复杂度
我们先分别算出第2层到h层的节点个数和该层节点的调整次数
然后再推出总的调整次数。
- 推导

所以向下建堆的时间复杂度是o(n),向上建堆的复杂度是o(n*logn).
所以以后我们都尽量使用向下调整建堆。因为他的效率更高。
1.3堆排序复杂度
现在我们来看一下我们堆排序的时间复杂度是多少呢?
- 推导
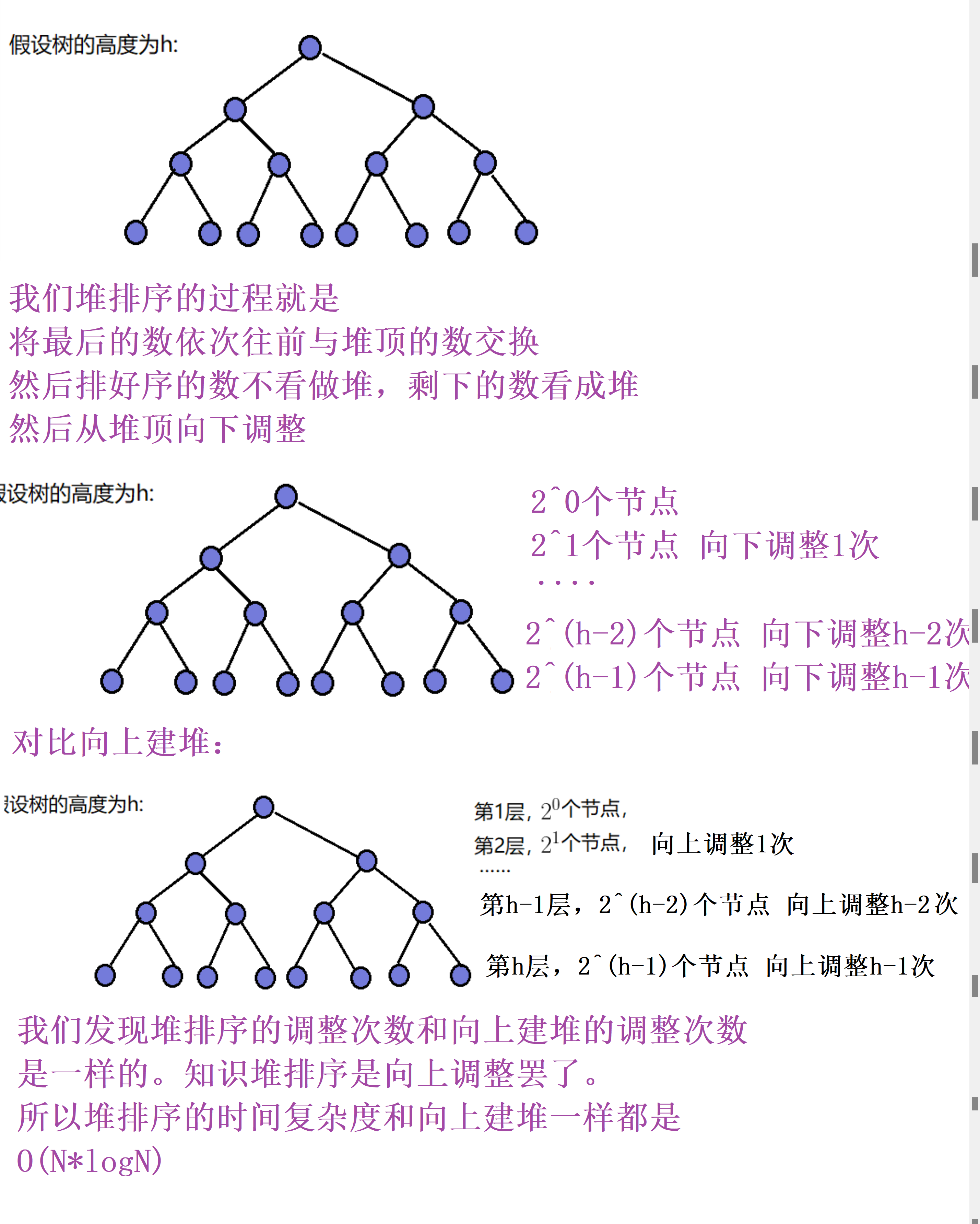
堆排序的复杂度是o(n*logn).
二.top-k问题
2.1思路分析
- 方法一
我们很容易想到直接排序然后取出前k个即可。
但是这个方法有个致命缺陷。
如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

我们发现这个方法在数据量太大的时候并不适用。
那有什么其他好的方法吗? - 方法二
最佳的方式就是用堆来解决,基本思路如下:
1 .用数据集合中前k个元素来建堆
前k个最大的元素,则建k个数的小堆
前k个最小的元素,则建k个数的大堆
2 . 用剩余的n-k个元素依次与堆顶元素来比较,
如果比堆顶元素还要大或小(小堆大 大堆小)则替换堆顶元素,然后向下调整重新建堆。
为什么呢?
- 证明

我们通过n-k次比较就可以筛选出n-k个不满足最大前k个数的数
剩下在堆的数就是最大的前k个。 - 疑问

我们用反证法可以得知这种情况不存在。
2.2代码实现
- 生成数据函数
我们先用srand生成不同的种子防止生成的随机数是伪随机数。
然后fopen打开文件。循环生成随机数然后写入文件即可。最后关闭文件。
void creatdata()
{
int n = 100000;//生成10万个数据
srand(time(0));//生成不同的种子
file* pf = fopen("test.txt", "w");//打开文件
for (int i = 0; i < n; i++)
{
int x = rand() % 100001+i;//生成随机数
fprintf(pf, "%d\n", x);//写数据
}
fclose(pf);//关闭文件
pf = null;
}
这样10万个数据就生成好了。
- 比较函数
我们先接收k。然后开好k个数是堆空间。
然后从文件读取前k个数并填充到堆里面。然后建堆
然后继续读取文件里的数据直到文件末尾(返回eof)
然后当数据大于堆顶元素是在进堆,然后重新调整建堆即可。
void test()
{
int k;
printf("请输入前k个数:");
scanf("%d", &k);
int* a = (int*)malloc(sizeof(int) * k);//开空间建堆
file* pf = fopen("test.txt", "r");
for (int i = 0; i < k; i++)
{
fscanf(pf, "%d", &a[i]);
}//填充数据
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
adjustdown(a, k, i);
}//建小堆
int x;
while (fscanf(pf, "%d", &x) !=eof)
{
if (x > a[0])
{
a[0] = x;
adjustdown(a, k, 0);
}
}//对比
for (int i = 0; i < k; i++)
{
printf("%d ", a[i]);
}//打印
}
- 检验
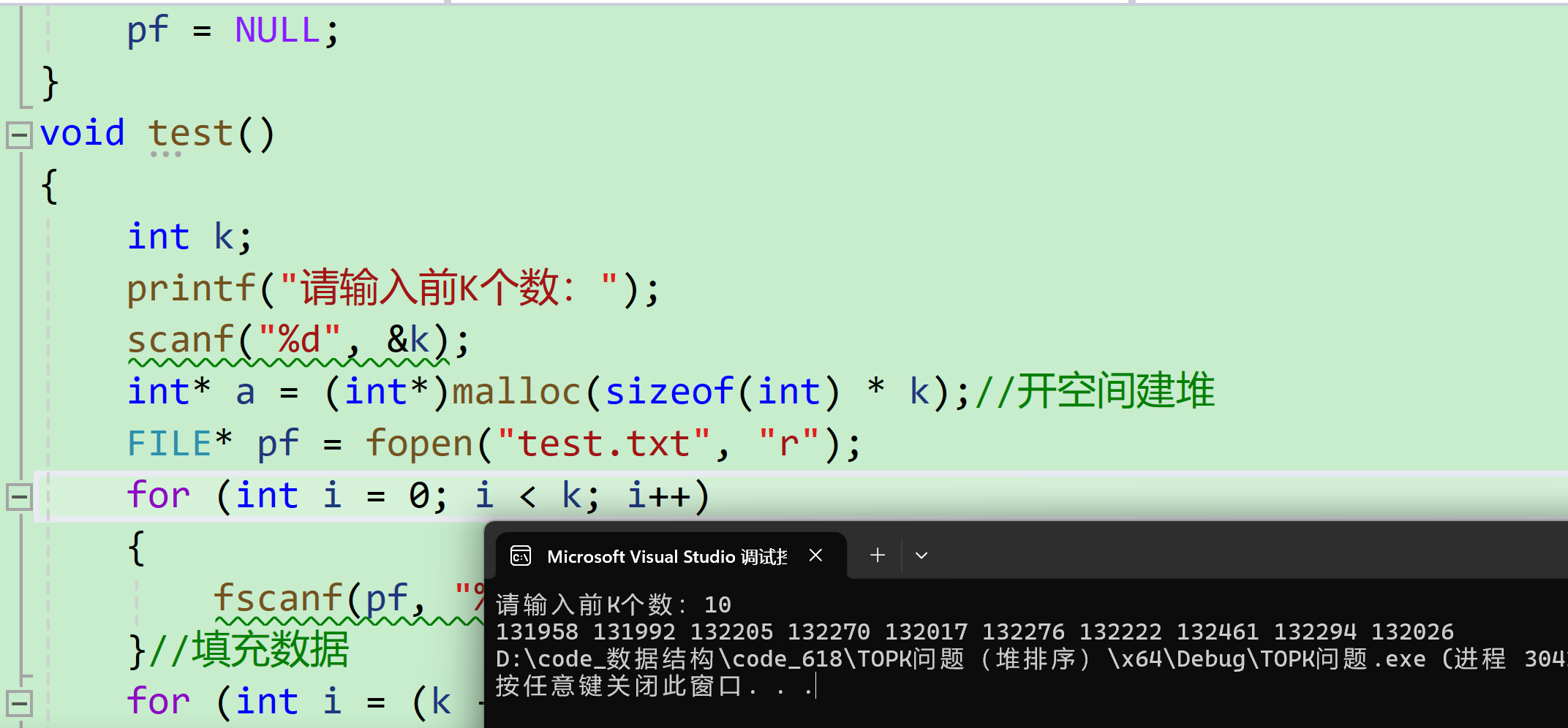
那我们如何确保这10个数一定是最大的呢?万一我们的算法写错不是最大的前10个数怎么办?










那我们就可以在不同的地方在一些k标点。
也就是k个很大的数,确保他们是最大的前k个。
然后只需要看结果是不是这k个数即可。
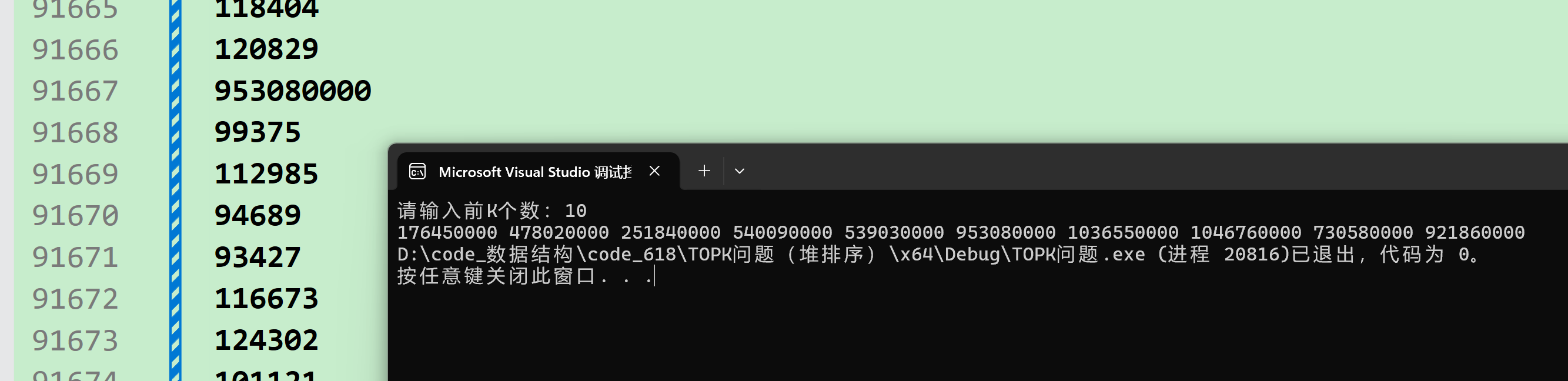
大家发现结果就是我们手动给的这10个数。说明我们的程序时没问题的。
后言





发表评论