文章目录
一、算法原理
(一)概念:
森林(forest)在计算机科学中,在数据结构中,可以看作是一组不相交的树(tree)的集合。每棵树都是独立的,它们之间没有边直接相连。在数据结构和算法中,森林经常用于表示和处理一系列没有共同祖先的节点集合。
并查集(union-find)是一种数据结构,用于高效地处理一些不交集的合并及查询问题。它主要用于处理一些动态连通性问题,如判断两个元素是否属于同一个集合,或者合并两个集合。
(二)quick_find算法
图中每一个结点代表一棵树,我们如果要连接两棵树,可以通过染色法将两个结点染成相同的颜色。

例:
连接结点1——结点4

连接结点2——结点5

连接结点4——结点5
代码演示
void init(int n) {
for (int i = 0; i <= n; i++) color[i] = i;
return ;
}
int find(int a) {
return color[a];
}
int merge(int a, int b, int n) {
int aa = find(a), bb = find(b);
if (aa == bb) return 0;
for (int i = 0; i <= n; i++) {
if (color[i] == aa) {
color[i] = bb;
}
}
return 1;
}
复杂度分析
查找判断:o(1)
联通操作:o(n)
(三)quick_union算法
图中每一个结点代表一棵树,我们如果要连接两棵树,可以通过将一棵树作为另一棵树的子树。
例:
注:默认将前一棵子树连接到后一颗上面
连接结点1——结点4

连接结点2——结点5
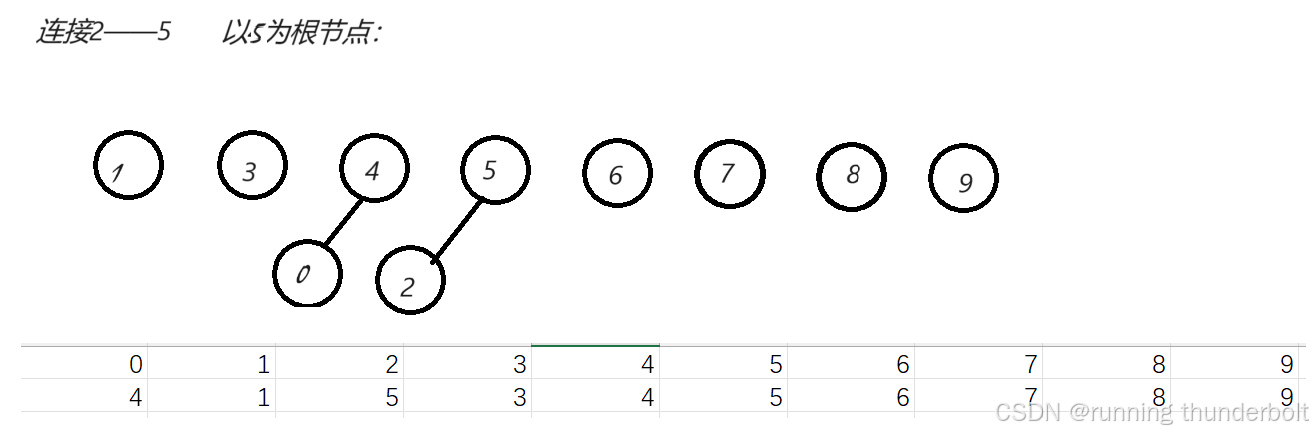
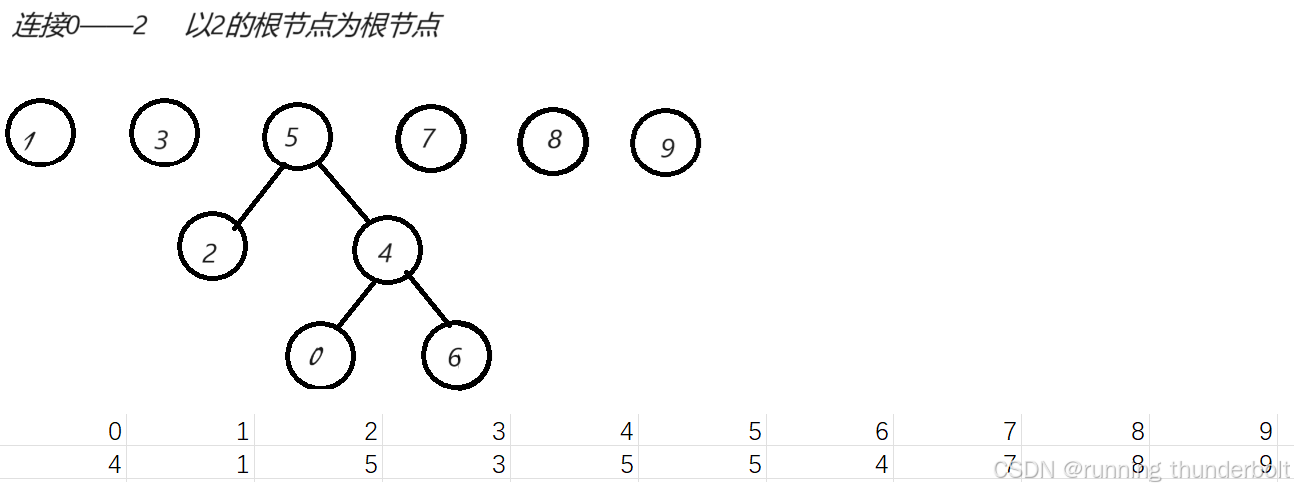
连接结点6——结点4
代码演示
void init(int n) {
for (int i = 0; i <= n; i++) {
fa[i] = i;
}
return ;
}
int find(int x) {
if (fa[x] == x) return x;
return find(fa[x]);
}
int merge(int a, int b) {
int aa = find(a), bb = find(b);
if (aa == bb) return 0;
fa[aa] = bb;
return 1;
}
复杂度分析
查找判断:
时间复杂度:最好情况o(lgn)最坏情况下是o(n),其中n是节点的总数。这是因为在极端情况下(如树退化为链表),从任意节点到根节点的路径可能包含n-1个边。
联通操作:o(1)
(四)并查集优化
按秩优化
通过加入每棵树的权重(即结点数量)使得每棵树不至于退化为链表。
代码演示
void init(int n) {
for (int i = 0; i <= n; i++) {
fa[i] = i;
size[i] = 1;
}
return ;
}
int find(int x) {
if (fa[x] == x) return x;
return find(fa[x]);
}
int merge(int a, int b) {
int aa = find(a), bb = find(b);
if (aa == bb) return 0;
if (size[aa] < size[bb]) {
fa[aa] = bb;
size[bb] += size[aa];
} else {
fa[bb] = aa;
size[aa] += size[bb];
}
return 1;
}
复杂度分析
查找判断:
时间复杂度:加入权重使得复杂度稳定在o(lgn)
联通操作:o(1)
路径压缩
在查找过程中每查找一条路径,就将路径上的所有结点放在根节点底下,使得数的整体高度变扁,查找单次的操作次数可能比较高,但是均摊时间复杂度为1。
代码演示
void init(int n) {
for (int i = 0; i <= n; i++) {
fa[i] = i;
size[i] = 1;
}
return ;
}
int find(int x) {
return fa[x] = (fa[x] == x ? x : find(fa[x]));
}
int merge(int a, int b) {
int aa = find(a), bb = find(b);
if (aa == bb) return 0;
if (size[aa] < size[bb]) {
fa[aa] = bb;
size[bb] += size[aa];
} else {
fa[bb] = aa;
size[aa] += size[bb];
}
return 1;
}
二、算法演示
(一)leetcode_128
代码演示
class unionset{
public:
unionset(int n):fa(n + 1),wight(n + 1){
for(int i = 0; i <= n; i++){
fa[i] = i;
wight[i] = 1;
}
}
int get(int i){
return fa[i] = (fa[i] == i ? i : get(fa[i]));
}
int merge(int a, int b){
/*
if(get(a) == get(b)) return 0;
fa[get(a)] = get(b);
wight[get(b)] += wight[get(a)];
return 1;
*/这里a的父节点更新,导致错误
int aa = get(a), bb = get(b);
if(get(a) == get(b)) return 0;
fa[aa] = bb;
wight[bb] += wight[aa];
return 1;
}
vector<int> fa,wight;
};
class solution {
public:
int longestconsecutive(vector<int>& nums) {
int n = nums.size(), cnt = 1;
if(n == 0) return 0;
unionset set(n);
unordered_map<int,int> map;
for(int i = 0; i < n; i++){
if(map.find(nums[i]) != map.end()) continue;
map[nums[i]] = cnt++;
if(map.find(nums[i] - 1) != map.end()) set.merge(map[nums[i] - 1], map[nums[i]]);
if(map.find(nums[i] + 1) != map.end()) set.merge(map[nums[i] + 1], map[nums[i]]);
}
int ans = 0;
for(int i = 0; i <= n; i++) if(set.wight[i] > ans) ans = set.wight[i];
return ans;
}
};
(二)leetcode_130
代码演示
class unionset{
public:
vector<int> fa;
unionset(int n):fa(n + 1){
for(int i = 0; i <= n; i++){
fa[i] = i;
}
}
int find(int x){
return fa[x] = (fa[x] == x ? x : find(fa[x]));
}
void merge(int a, int b){
fa[find(a)] = find(b);
return;
}
};
class solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size(), m = board[0].size(), ind;
unionset u(n*m);
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(board[i][j] != 'o') continue;
ind = i * m + j + 1;
if(i == 0 || i == n - 1) u.merge(ind, 0);
if(j == 0 || j == m - 1) u.merge(ind, 0);
if(j < (m - 1) && board[i][j + 1] == 'o') u.merge(ind, ind + 1);
if(i < (n - 1) && board[i + 1][j] == 'o') u.merge(ind, ind + m);
}
}
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(board[i][j] != 'o') continue;
ind = i * m + j + 1;
if(u.find(ind) != u.find(0)) board[i][j] = 'x';
}
}
return;
}
};
(三)hzoj_322
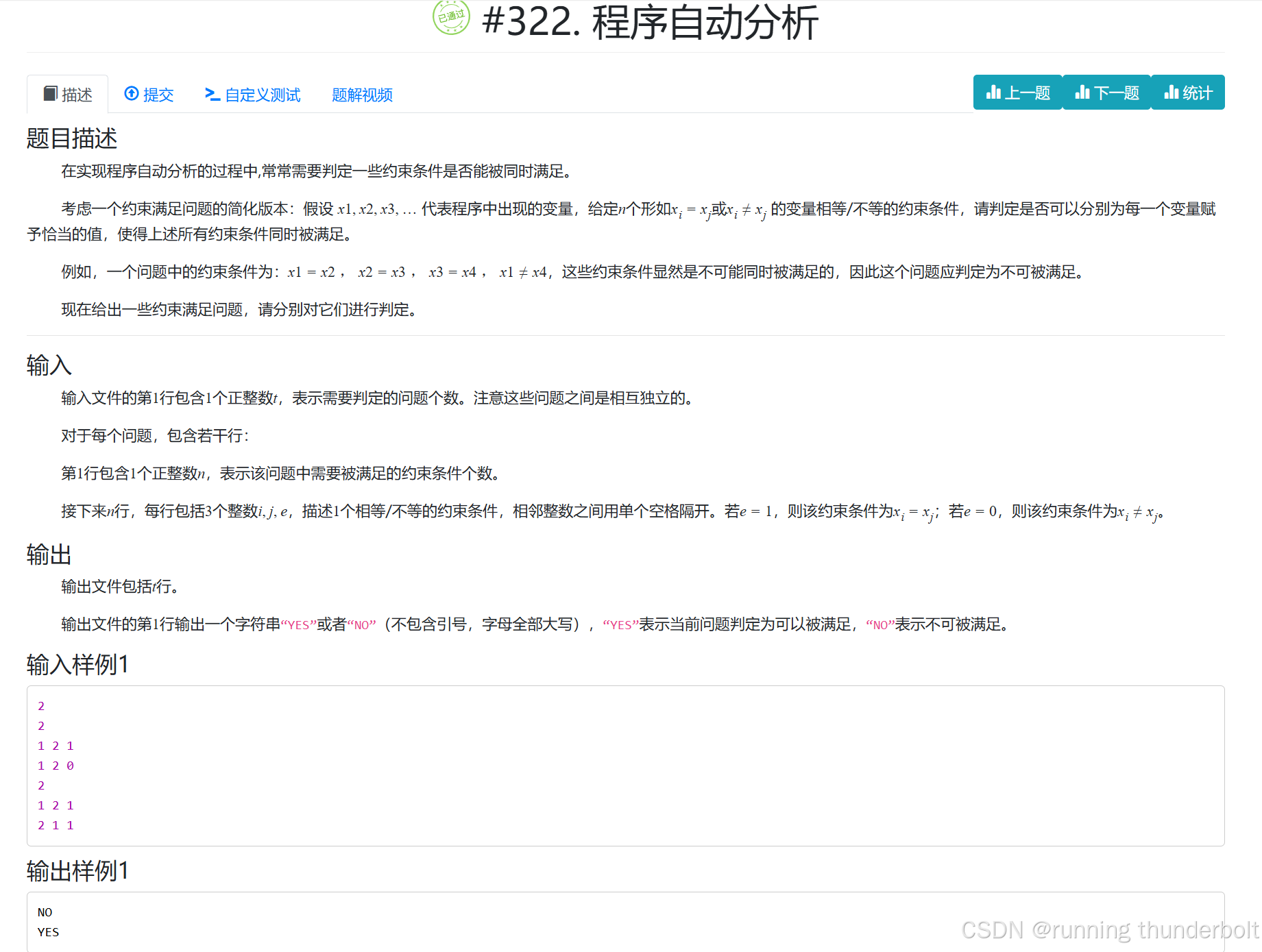
代码演示
class unionset {
public :
unionset(int n) : fa(n + 1) {
for (int i = 0; i <= n; i++) fa[i] = i;
}
int get(int x) {
return fa[x] = (fa[x] == x ? x : get(fa[x]));
}
void merge(int a, int b) {
fa[get(a)] = get(b);
}
vector<int> fa;
};
struct data {
int i, j, e;
};
void solve() {
int n, cnt = 0;
scanf("%d", &n);
vector<data> arr(n);
unordered_map<int, int> h;
for (int i = 0; i < n; i++) {
data &x = arr[i];
scanf("%d%d%d", &x.i, &x.j, &x.e);
if (h.find(x.i) == h.end()) h[x.i] = cnt++;
if (h.find(x.j) == h.end()) h[x.j] = cnt++;
}
unionset u(2 * n);
for (int i = 0; i < n; i++) {
if (arr[i].e == 0) continue;
u.merge(h[arr[i].i], h[arr[i].j]);
}
int flag = 1;
for (int i = 0; i < n && flag; i++) {
if (arr[i].e == 1) continue;
if (u.get(h[arr[i].i]) == u.get(h[arr[i].j])) {
flag = 0;
}
}
printf("%s\n", flag ? "yes" : "no");
return ;
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
solve();
}
return 0;
}
三、小结
用并查集解决连通性问题是一个很好的方法,如果文章有帮助,就给个免费的赞吧!小编和大家一起进步!







发表评论