机器学习之逻辑回归

一、逻辑回归算法原理

1. 1 逻辑回归的基本概念

在机器学习领域，逻辑回归是一个基础且重要的分类算法。它通常用于解决二分类问题，即输出结果只有两种可能性的问题。尽管名为“回归”，逻辑回归实际上是一种分类方法，而不是回归方法。

逻辑回归基于一个关键假设：数据可以通过线性组合的logistic函数进行建模。具体来说，逻辑回归模型通过将输入特征的线性组合传递给sigmoid函数（也称为logistic函数），从而预测出属于某一类的概率。我们顺便来说一下回归与分类在输出结果上的不同之处。

• 回归：回归任务的目标是预测一个连续值。例如，根据房屋的特征来预测其市场价格，或者预测明天的具体气温。
• 分类：分类任务则是将数据点分配到预定义的类别中是离散值。比如，根据邮件的内容判断其是否为垃圾邮件，或者预测天气属于晴、阴还是雨等离散类别。

1.2 数学表达

逻辑回归的数学表达式可以写作：

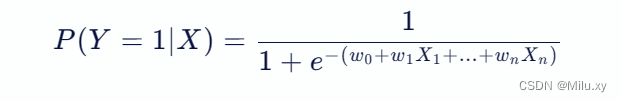
其中：

• p(y=1∣x) 是在给定输入 x 的情况下，输出为1（正类）的概率。
• w0​,w1​,...,wn​ 是模型参数，通过训练数据学习得到。
• x1​,...,xn​ 是输入特征。

1.3 工作原理

逻辑回归 = 线性回归 + sigmoid函数

a. 线性回归

首先，逻辑回归模型计算输入特征的加权和。这个过程类似于线性回归中的操作，但逻辑回归的目的不是预测具体的数值，而是用来估计概率。

b. sigmoid函数

接着，线性组合的结果被传递到一个sigmoid函数中。sigmoid函数可以将任何实数映射到(0,1)区间内，这使得输出可以被解释为一个概率值。下面是该函数的图像：

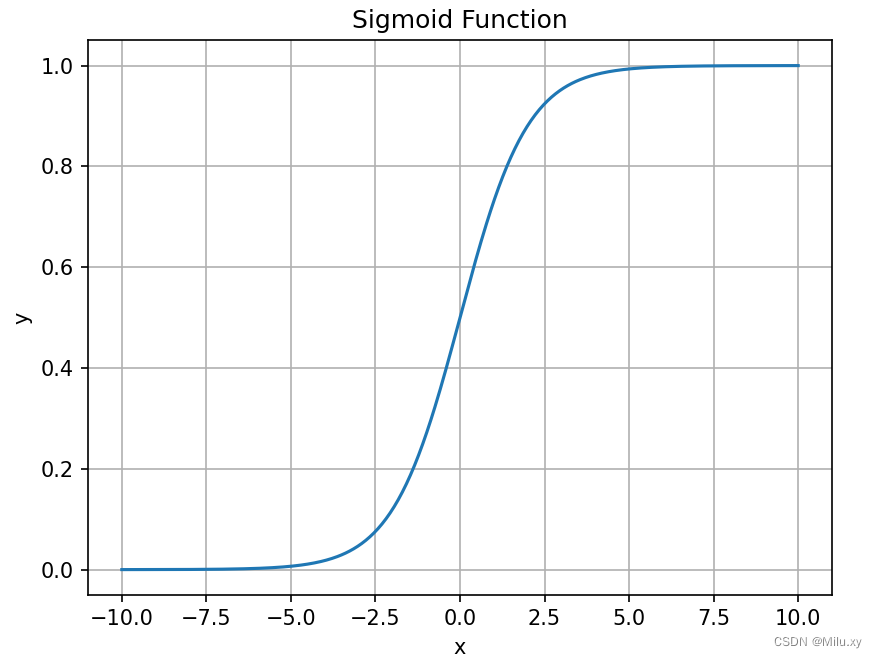
c. 概率解释

最终，模型输出一个概率值，表示给定输入属于正类的可能性。在实际应用中，通常会设置一个阈值（如0.5），如果计算出的概率大于这个阈值，则预测该样本属于正类，否则属于负类。

二、 损失函数与优化

2.1 交叉熵损失

对于二分类问题，我们使用交叉熵损失来衡量模型预测的概率分布与真实概率分布之间的差异。对于单个样本，交叉熵损失可以表示为：

l(y,hθ​(x))=−ylog(hθ​(x))−(1−y)log(1−hθ​(x))

• 当 y=1 时，损失简化为 −log(hθ​(x))
• 当 y=0 时，损失简化为 −log(1−hθ​(x))

2.2 损失函数推导

在机器学习中，我们通常使用所有样本的平均损失作为优化目标。因此，对于包含 m 个样本的数据集，逻辑回归的损失函数（也称为成本函数）可以表示为：

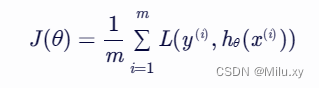
将单个样本的交叉熵损失代入上式，得到：

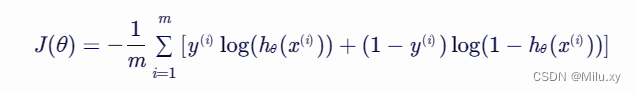
2.3 梯度下降法优化

为了找到使损失函数 j(θ) 最小的参数 θ，我们通常使用梯度下降算法。这需要我们计算 j(θ) 关于 θ 的梯度。梯度下降算法会沿着梯度的反方向更新 θ，从而逐渐减小损失函数的值。

梯度计算

计算 j(θ) 关于 θj​ 的偏导数（即梯度），得到：

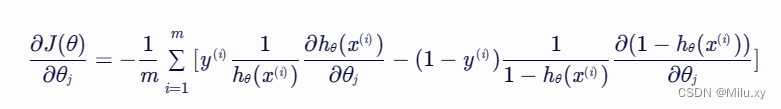
由于 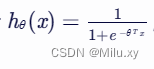，我们可以进一步计算​：

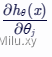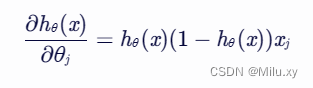
将上述结果代入梯度表达式中，得到：

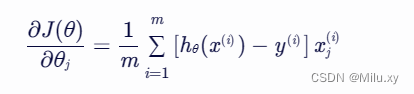
这个梯度表达式将用于梯度下降算法中，以更新逻辑回归的参数 θ。

三、算法实现

3.1 初始化函数

将sigmoid函数进行定义

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

3.2 初始的方法

初始化方法，用于设置学习率和迭代次数。学习率是梯度下降过程中参数更新的步长，迭代次数是梯度下降的迭代次数。

    def __init__(self, learning_rate=0.003, iterations=100):
        self.learning_rate = learning_rate  # 学习率
        self.iterations = iterations  # 迭代次数

3.3 训练方法与模型

输入参数为特征矩阵x和目标向量y。在这个方法中，首先初始化权重和偏置，然后使用梯度下降法更新权重和偏置，最后计算损失函数并打印。

    def fit(self, x, y):
        # 初始化参数
        self.weights = np.random.randn(x.shape[1])
        self.bias = 0

        # 梯度下降
        for i in range(self.iterations):
            # 计算sigmoid函数的预测值, y_hat = w * x + b
            y_hat = sigmoid(np.dot(x, self.weights) + self.bias)

            # 计算损失函数
            loss = (-1 / len(x)) * np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))

            # 计算梯度
            dw = (1 / len(x)) * np.dot(x.t, (y_hat - y))
            db = (1 / len(x)) * np.sum(y_hat - y)

            # 更新参数
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

            # 打印损失函数值
            if i % 10 == 0:
                print(f"loss after iteration {i}: {loss}")

 3.4 预测方法

用于对输入的特征矩阵x进行预测。输出为预测结果向量y_hat。

    def predict(self, x):
        y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
        y_hat[y_hat >= 0.5] = 1
        y_hat[y_hat < 0.5] = 0
        return y_hat

 3.5 评估方法

评估方法，用于计算预测结果的准确率。输入参数为预测结果向量y_pred和真实目标向量y。输出为准确率。

    def score(self, y_pred, y):
        accuracy = (y_pred == y).sum() / len(y)
        return accuracy

3.6 完整代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 设置随机种子
seed_value = 2023
np.random.seed(seed_value)


# sigmoid激活函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))


# 定义逻辑回归算法
class logisticregression:
    def __init__(self, learning_rate=0.003, iterations=100):
        self.learning_rate = learning_rate  # 学习率
        self.iterations = iterations  # 迭代次数

    def fit(self, x, y):
        # 初始化参数
        self.weights = np.random.randn(x.shape[1])
        self.bias = 0

        # 梯度下降
        for i in range(self.iterations):
            # 计算sigmoid函数的预测值, y_hat = w * x + b
            y_hat = sigmoid(np.dot(x, self.weights) + self.bias)

            # 计算损失函数
            loss = (-1 / len(x)) * np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))

            # 计算梯度
            dw = (1 / len(x)) * np.dot(x.t, (y_hat - y))
            db = (1 / len(x)) * np.sum(y_hat - y)

            # 更新参数
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

            # 打印损失函数值
            if i % 10 == 0:
                print(f"loss after iteration {i}: {loss}")

    # 预测
    def predict(self, x):
        y_hat = sigmoid(np.dot(x, self.weights) + self.bias)
        y_hat[y_hat >= 0.5] = 1
        y_hat[y_hat < 0.5] = 0
        return y_hat

    # 精度
    def score(self, y_pred, y):
        accuracy = (y_pred == y).sum() / len(y)
        return accuracy


# 导入数据
iris = load_iris()
x = iris.data[:, :2]
y = (iris.target != 0) * 1

# 划分训练集、测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.15, random_state=seed_value)

# 训练模型
model = logisticregression(learning_rate=0.03, iterations=1000)
model.fit(x_train, y_train)

# 结果
y_train_pred = model.predict(x_train)
y_test_pred = model.predict(x_test)

score_train = model.score(y_train_pred, y_train)
score_test = model.score(y_test_pred, y_test)

print('训练集accuracy: ', score_train)
print('测试集accuracy: ', score_test)

# 可视化决策边界
x1_min, x1_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
x2_min, x2_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 100), np.linspace(x2_min, x2_max, 100))
z = model.predict(np.c_[xx1.ravel(), xx2.ravel()])
z = z.reshape(xx1.shape)
plt.contourf(xx1, xx2, z, cmap=plt.cm.spectral)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.spectral)
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.show()

3.6运行结果

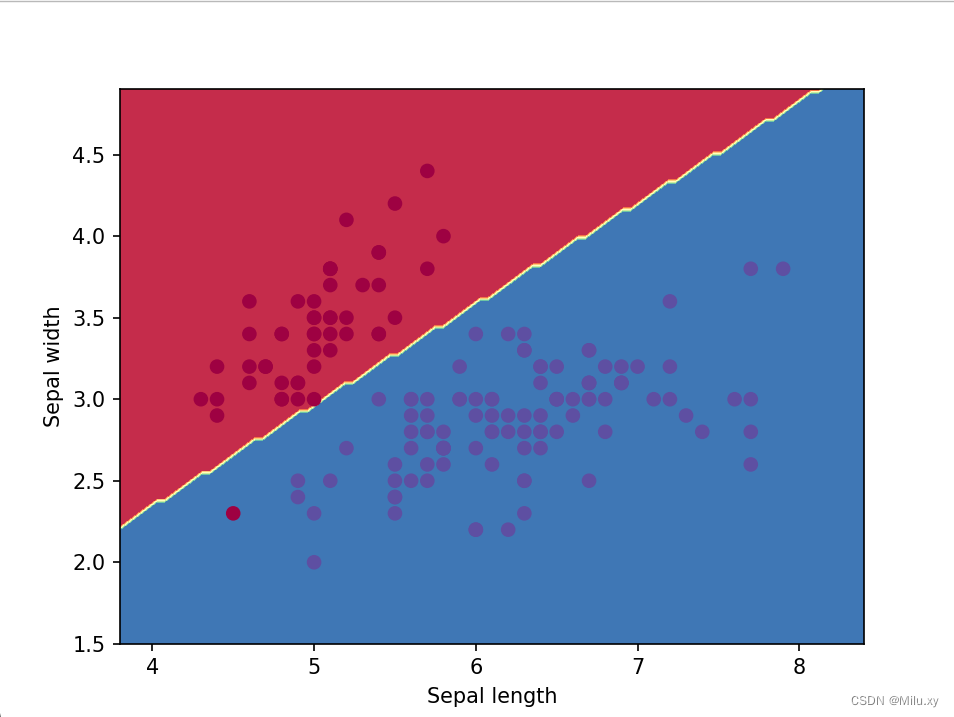
 四、总结

4.1 优点与局限性

优点：逻辑回归的优点包括其简单性、易于理解以及高效性。它不需要复杂的数学运算，因此在处理大型数据集时表现良好。

局限性：逻辑回归也有局限性，比如它不能很好地处理非线性关系，且对于高度相关的输入特征可能会产生多重共线性问题。

4.2 总结

逻辑回归是一个强大的机器学习算法，尤其适用于二分类问题。通过理解和应用逻辑回归的基本原理，我们可以构建出能够预测分类结果的模型。虽然它在某些复杂场景下可能不是最佳选择，但在许多实际应用中，逻辑回归仍然是快速而有效的解决方案。

4.3 结语

逻辑回归作为机器学习中的一个经典算法，它的简洁性和效率使其成为初学者和专家都青睐的工具。无论是在学术研究还是在业界实践中，掌握逻辑回归的原理都是迈向高级机器学习应用的重要一步。