我要评论
前言
图像配准方法分为三种：基于灰度信息方法、基于变换域方法和基于特征方法。 基于灰度信息方法是直接根据图像或图像块灰度信息进行像素上的对齐，该方法主要思想是直接最小化图像信息差异。然而，图像信息差异的判断准则衍生出不同的配准方法。常见的基于灰度信息的图像配准方法包括互相关法、互信息法和误差平方和法。
本节将分别对互相关法、互信息法和误差平方和算法展开介绍，并通过matlab进行演示。
一、互相关法
在信号处理中，互相关可以测量两个信号之间的相似性，寻找局部最大值得到信号间的相对位移。类似地，在图像处理领域，通过计算模板图像和目标图像之间的互相关值，也可以判断目标图像相对模板图像的位移值。此外，互相关函数和卷积运算类似，也是两个序列滑动相乘。互相关的两个序列都不翻转，直接滑动相乘，求和。卷积的其中一个序列先翻转，再滑动相乘。计算公式如下：
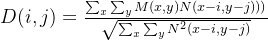
其中，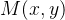
是待配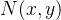准图像，
是基准图像
matlab程序如下：
img1 = im2gray(imread("0000000000.png"));
img2 = im2gray(imread("0000000021.png"));
montage({img1, img2});
c = normxcorr2(img1, img2);
surf(c);
shading flat;
[ypeak,xpeak] = find(c==max(c(:)));
yoffset = ypeak-size(img1,1);
xoffset = xpeak-size(img2,2);
imshow(img2)
drawrectangle(gca,'position',[xoffset,yoffset,size(img1,2),size(img1,1)], 'facealpha',0);仿真结果如下：
二、互信息法
互信息是信息论中的重要概念，描述两个系统之间的相关性，或相互包含信息的多少。在图像配准中，两幅图的互信息是通过它们的熵以及联合熵，来反映它们之间信息的相互包含程度。对应图像x和y，互信息表示为：
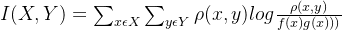
其中，f(x)和g(x)分别表示概率密度函数；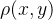
表示联合概率密度函数。
matlab程序如下：
clear all;
img1 = rgb2gray(imread("0000000000.png")); % rgb图转灰度图
[a,b] = size(img1); % 图片尺寸
m = 60; % 原图截取初始x位置
n = 80; % 原图截取初始y位置
s = 44; % 截取长度
img2 = img1(m:m+s-1,n:n+s-1); % 获取截取图像
imshow(img2); % 展示截取图像
et = entropy(img2); % 计算img2熵值
for i = 1: a-s % 遍历每行
for j = 1: b-s % 遍历每列
img3 = img1(i:i+s-1,j:j+s-1); % 构造和img2同尺寸的可移动图像
es = entropy(img3); % 计算img3熵
histq = zeros(256,256); % 初始化灰度值计数矩阵
%% 对两个图像的存在的相同灰度值进行计数
for k = 1:s %
for l = 1:s
x = img2(k,l) + 1; % 若img2(1,1)灰度值为10，则对应x轴11； 考虑灰度值范围为0-255转为1-256
y = img3(k,l) + 1; % 若img3(1,1)灰度值为15，则对应y轴16；
% (11,16)进行计数加1
histq(x,y) = histq(x,y) + 1;
end
end
%%
p = histq./sum(sum(histq)); % 联合概率密度
est = -sum(sum(p.*log(p+eps))); %联合熵，越小越相似
mi(i,j) = es + et - est; % 互信息越大，越相似
nmi(i,j) = (es + et)/est; % nmi越大越相似
ecc(i,j) = 2*mi(i,j)/(es+et); % ecc越大越相似
end
end
max_mi = max(max(mi)); % 最大的mi
max_nmi = max(max(nmi)); % 最大的nmi
max_ecc = max(max(ecc)); % % 最大的ecc
[x1,y1] = find(mi == max_mi); % 最大的mi坐标
[x2,y2] = find(nmi == max_nmi); % 最大的nmi坐标
[x3,y3] = find(ecc == max_ecc); % % 最大的ecc坐标
figure;imshow(img1);hold on; rectangle('position',[y1,x1,s-1,s-1],'edgecolor','r');title('mi配准图');hold off;
figure;imshow(img1);hold on; rectangle('position',[y2,x2,s-1,s-1],'edgecolor','r');title('nmi配准图');hold off;
figure;imshow(img1);hold on; rectangle('position',[y3,x3,s-1,s-1],'edgecolor','r');title('ecc配准图');hold off;
仿真结果如下：
三、误差平方和法
误差平方和法，顾名思义，计算待匹配图像和基准图像的误差平方和，具体表达式如下：
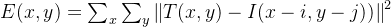
matlab程序如下：
clear all;
img1 = rgb2gray(imread("0000000000.png")); % rgb图转灰度图
[a,b] = size(img1); % 图片尺寸
m = 60; % 原图截取初始x位置
n = 80; % 原图截取初始y位置
s = 114; % 截取长度
img2 = img1(m:m+s-1,n:n+s-1); % 获取截取图像
imshow(img2); % 展示截取图像
min_res = inf;
for i = 1: a-s % 遍历每行
for j = 1: b-s % 遍历每列
img3 = img1(i:i+s-1,j:j+s-1); % 构造和img2同尺寸的可移动图像
res = sum(sum((img2-img3).^2)); % ssd相似函数
if res < min_res
min_res = res;
best_x = i;
best_y = j;
end
end
end
figure;imshow(img1);hold on; rectangle('position',[best_y,best_x,s-1,s-1],'edgecolor','r');hold off;仿真结果如下：
总结
基于灰度的图像方法容易实现，但同样存在不足。该方法对成像条件(光照，遮挡)、图像形变旋转以及噪声极其敏感，同时具有较高的计算复杂度。
发表评论