之前写过b+树的基础概念和图解,数据库中b+树与索引,这里我继续用用c++代码实现一个简单的b+树,通过代码深入了解b+树,包含插入、查找和分裂的过程,我也写了详细的代码注释,以及过程的思路介绍。
这里创建一个节点的结构体,是b+树叶子节点和非叶子节点的内部结构
using namespace std;
const int m = 4; // b+树的阶数,m-1是b+树中每个节点最多存储的关键字个数
struct node {
int n; // 当前节点中关键字的个数
vector<int> keys; // 关键字
vector<node*> children; // 子节点
node() {
n = 0; //初始化关键词个数,空节点
keys.resize(m-1); // 初始化keys数组大小为m-1,及4阶的b+树中,节点内最多3个关键词
children.resize(m); // 初始化children数组大小为m,及4阶的b+树中,最多有4个子树
}
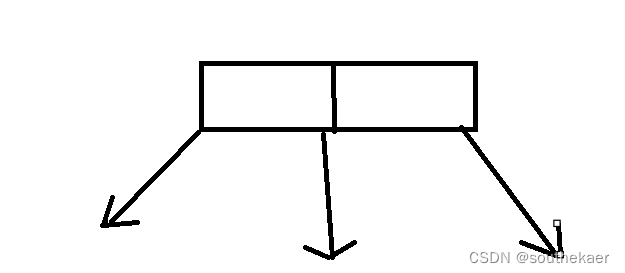
};初始化的节点就如图所示,关键词为2个,子节点为3个,都为空
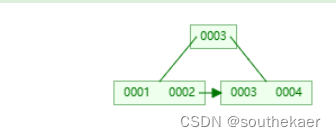
这颗b+树中,根节点内的关键词个数就是1个,而他的子节点就是2个
下面定义了一个b+树的类,里面有insert插入和search查询的成员函数
class bplustree {
public:
bplustree() {
root = nullptr; //根节点
}
~bplustree() { //析构函数
}
node* root;
// 插入关键字
void insert(int key) {
if (root == nullptr) { // 如果根节点为空,创建新节点作为根节点
root = new node();
root->n = 1;
root->keys[0] = key;
} else {
node* node = findleafnode(key); // 查找包含关键字的叶子节点,为后续插入找到节点
insertinnode(node, key); // 在叶子节点中插入关键字
}
}
// 查找关键字
bool search(int key) {
node* node = findleafnode(key); // 查找包含关键字的叶子节点
for (int i = 0; i < node->n; i++) { // 遍历叶子节点中的关键字
if (node->keys[i] == key) { // 如果找到目标关键字,返回true
return true;
}
}
return false; // 否则返回false
}插入的时候,如果根节点为空,创建新的根节点,不为空则需要先找到插入位置,再继续进行插入:
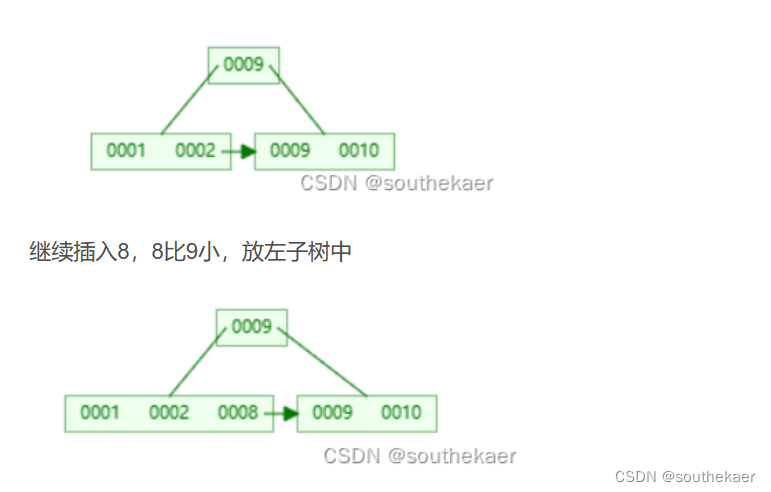
这是查找到所需要插入的节点
1.从根节点开始查找
2.对所插入的值和当前节点的关键词的值进行比较,并用 i 记录,比较后继续跳到当前节点的第i个子节点
3当当前节点是叶子节点,也就是不能继续向下查找时,返回当前节点
// 查找包含关键字的叶子节点
node* findleafnode(int key) {
node* node = root;
while (node->children[0] != nullptr) { // 如果当前节点不是叶子节点,继续向下查找
int i = 0;
while (i < node->n && key >= node->keys[i]) { // 找到目标关键字应该插入的子节点
i++;
}
node = node->children[i];
}
return node; // 返回叶子节点
}而查找关键词则需要在查询到节点后,遍历节点内的元素进行关键词的比较
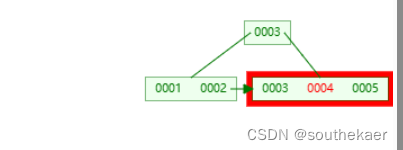
查询4:
找到根节点的右子树节点,然后进行遍历,比较,查到到4
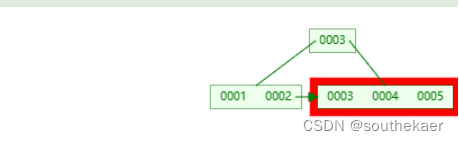
下面是向节点内插入关键字:
1 从最右侧开始比较,如果插入值小于当前关键词的值,则将当前关键词右移一位,并继续比较,直到对比完第一个关键词或对比到不小于的关键词,将插入值保存
2 如果关键词个数大于等于阶数,开始分裂节点
// 在节点中插入关键字
void insertinnode(node* node, int key) {
int i = node->n - 1; // 从当前节点中最右侧关键字开始遍历
while (i >= 0 && key < node->keys[i]) { // 如果待插入的关键字比当前关键字小,则将当前关键字向右移动一位
node->keys[i + 1] = node->keys[i];
i--;
}
node->keys[i + 1] = key; // 将待插入的关键字插入到空出来的位置
node->n++;
if (node->n >= m) { // 如果当前节点中关键字个数超过了m-1,则需要分裂节点
splitnode(node);
}
}
往下面这个节点插入 值 0
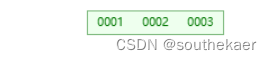
遍历节点内关键词,跟3进行对比,小于3,继续跟2对比,比2小,继续跟1对比,比1小,结束遍历,插入在1的左边

叶子节点的关键词个数大于等于阶数4,开始分裂
下面是分裂节点所需要的查找父节点、查找节点在父节点中的位置的两个函数
因为分裂节点的时候,是需要把一个关键词放入父节点中
// 递归查找节点的父节点
node* getparent(node* node, node* child) {
for (int i = 0; i <= node->n; i++) {
if (node->children[i] == child) { // 如果当前节点是子节点的父节点,返回当前节点
return node;
}else if (node->children[i] != nullptr && child->keys[0] < node->keys[i]){ // 否则,继续向下查找
return getparent(node->children[i], child);
}
}
return nullptr;
}
// 查找节点在父节点中的位置
int getchildindex(node* parent, node* child) {
for (int i = 0; i <= parent->n; i++) {
if (parent->children[i] == child) { // 如果当前节点是子节点的父节点,返回当前节点的位置
return i;
}
}
return -1;
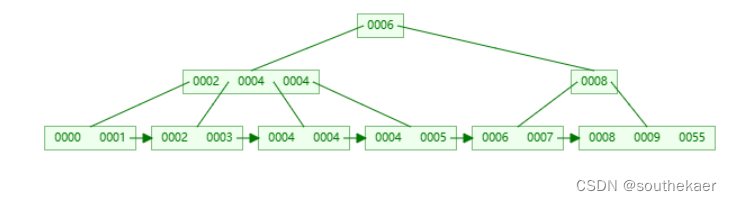
}插入时候分裂节点过程详述:
1 找到节点中中间位置以及关键字,这个中间位置的关键字后面是需要插入到父节点中,如分裂的节点是根节点则需要创新一个新的根节点存放这个中间位置的关键字
2 创建左字节点,存放小于中间关键字的关键字,并接到父节点
3 创建右字节点,存放大于等于中间关键字的关键字,并接到父节点
4 如果插入值的父节点的关键字的个数,大于阶数,需要继续分裂
插入时候分裂节点遇到的两种情况详解:
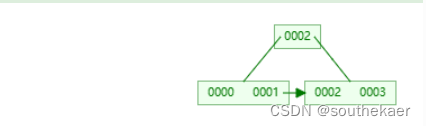
第一种情况,分裂的节点是根节点:

1 找到中间值 2 ,由于是根节点分裂,则需要创建新的根节点存储2
2 创建左字节点,存放小于中间值2的值,并接入父节点
3 创建右字节点,存放大于等于中间值2的值,并接入父节点
第二种情况,分裂的节点不是根节点:
插入值4
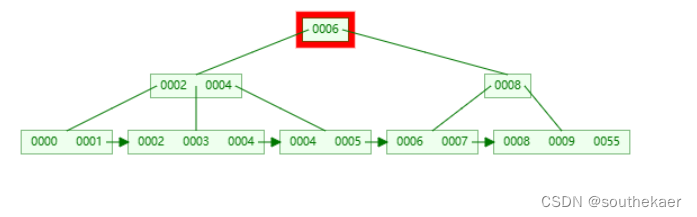
值插入叶子节点中,发现叶子节点需要分裂
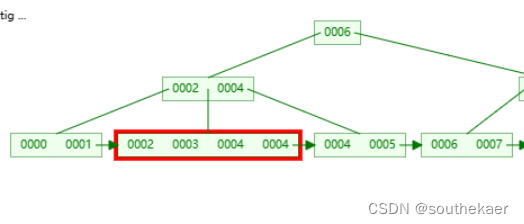
1 将中间值4插入父节点中,查询到此节点的父节点,并插入,如果父节点也需要分裂,则先递归分裂父节点
2 创建左子节点接入父节点
3 创建右字节点接入父节点
void splitnode(node* node) {
int mid = node->n / 2; // 找到中间位置
int key = node->keys[mid]; // 中间关键字
node* left = new node(); // 创建左子节点
left->n = mid;
for (int i = 0; i < mid; i++) { // 将左半部分关键字和子节点复制到新的节点中
left->keys[i] = node->keys[i];
left->children[i] = node->children[i];
}
left->children[mid] = node->children[mid];
node* right = new node(); // 创建右子节点
right->n = node->n - mid - 1;
for (int i = mid + 1; i < node->n; i++) { // 将右半部分关键字和子节点复制到新的节点中
right->keys[i - mid - 1] = node->keys[i];
right->children[i - mid - 1] = node->children[i];
}
right->children[node->n - mid - 1] = node->children[node->n];
if (node == root) { // 如果当前节点是根节点,需要创建新的根节点
root = new node();
root->n = 1;
root->keys[0] = key;
root->children[0] = left;
root->children[1] = right;
} else { // 否则,将中间关键字插入到父节点中,并将左右子节点插入到父节点中
node* parent = getparent(root, node);
insertinnode(parent,key); // 插入中间关键字到父节点中
int index = getchildindex(parent, node); // 获取当前节点在父节点中的位置
parent->children[index] = left; // 将左子节点插入到父节点中
parent->children[index + 1] = right; // 将右子节点插入到父节点中
delete node; // 删除当前节点
}
}下面是代码汇总:
#include <iostream>
#include <vector>
using namespace std;
const int m = 4; // b+树的阶数,m-1是b+树中每个节点最多存储的关键字个数
struct node {
int n; // 当前节点中关键字的个数
vector<int> keys; // 关键字
vector<node*> children; // 子节点
node() {
n = 0; //初始化关键词个数,空节点
keys.resize(m-1); // 初始化keys数组大小为m-1
children.resize(m); // 初始化children数组大小为m
}
};
class bplustree {
public:
bplustree() {
root = nullptr; //根节点
}
~bplustree() { //析构函数
}
node* root;
// 插入关键字
void insert(int key) {
if (root == nullptr) { // 如果根节点为空,创建新节点作为根节点
root = new node();
root->n = 1;
root->keys[0] = key;
} else {
node* node = findleafnode(key); // 查找包含关键字的叶子节点
insertinnode(node, key); // 在叶子节点中插入关键字
}
}
// 查找关键字
bool search(int key) {
node* node = findleafnode(key); // 查找包含关键字的叶子节点
for (int i = 0; i < node->n; i++) { // 遍历叶子节点中的关键字
if (node->keys[i] == key) { // 如果找到目标关键字,返回true
return true;
}
}
return false; // 否则返回false
}
private:
// 在节点中插入关键字
void insertinnode(node* node, int key) {
int i = node->n - 1; // 从当前节点中最右侧关键字开始遍历
while (i >= 0 && key < node->keys[i]) { // 如果待插入的关键字比当前关键字小,则将当前关键字向右移动一位
node->keys[i + 1] = node->keys[i];
i--;
}
node->keys[i + 1] = key; // 将待插入的关键字插入到空出来的位置
node->n++;
if (node->n >= m) { // 如果当前节点中关键字个数超过了m-1,则需要分裂节点
splitnode(node);
}
}
// 分裂节点
void splitnode(node* node) {
int mid = node->n / 2; // 找到中间位置
int key = node->keys[mid]; // 中间关键字
node* left = new node(); // 创建左子节点
left->n = mid;
for (int i = 0; i < mid; i++) { // 将左半部分关键字和子节点复制到新的节点中
left->keys[i] = node->keys[i];
left->children[i] = node->children[i];
}
left->children[mid] = node->children[mid];
node* right = new node(); // 创建右子节点
right->n = node->n - mid - 1;
for (int i = mid + 1; i < node->n; i++) { // 将右半部分关键字和子节点复制到新的节点中
right->keys[i - mid - 1] = node->keys[i];
right->children[i - mid - 1] = node->children[i];
}
right->children[node->n - mid - 1] = node->children[node->n];
if (node == root) { // 如果当前节点是根节点,需要创建新的根节点
root = new node();
root->n = 1;
root->keys[0] = key;
root->children[0] = left;
root->children[1] = right;
} else { // 否则,将中间关键字插入到父节点中,并将左右子节点插入到父节点中
node* parent = getparent(root, node);
insertinnode(parent,key); // 插入中间关键字到父节点中
int index = getchildindex(parent, node); // 获取当前节点在父节点中的位置
parent->children[index] = left; // 将左子节点插入到父节点中
parent->children[index + 1] = right; // 将右子节点插入到父节点中
delete node; // 删除当前节点
}
}
// 查找包含关键字的叶子节点
node* findleafnode(int key) {
node* node = root;
while (node->children[0] != nullptr) { // 如果当前节点不是叶子节点,继续向下查找
int i = 0;
while (i < node->n && key >= node->keys[i]) { // 找到目标关键字应该插入的子节点
i++;
}
node = node->children[i];
}
return node; // 返回叶子节点
}
// 查找节点的父节点
node* getparent(node* node, node* child) {
for (int i = 0; i <= node->n; i++) {
if (node->children[i] == child) { // 如果当前节点是子节点的父节点,返回当前节点
return node;
}else if (node->children[i] != nullptr && child->keys[0] < node->keys[i]){ // 否则,继续向下查找
return getparent(node->children[i], child);
}
}
return nullptr;
}
// 查找节点在父节点中的位置
int getchildindex(node* parent, node* child) {
for (int i = 0; i <= parent->n; i++) {
if (parent->children[i] == child) { // 如果当前节点是子节点的父节点,返回当前节点的位置
return i;
}
}
return -1;
}
};


发表评论