
✨个人主页:
目录
上一弹我们学习了直接插入排序,通过时空复杂度分析,时间复杂度为o(n^2),一般情况效率较低,有没有对直接插入排序进行优化的排序呢???没错,我们这一弹讲解的排序就是对直接插入排序的优化的排序!!!
1、希尔排序( 缩小增量排序 )
希尔排序是一种基于插入排序的算法,通过引入增量的概念来改进插入排序的性能
动图如下:
实现思路
1.1、预排序实现
预排序:
假设当前增量为5:
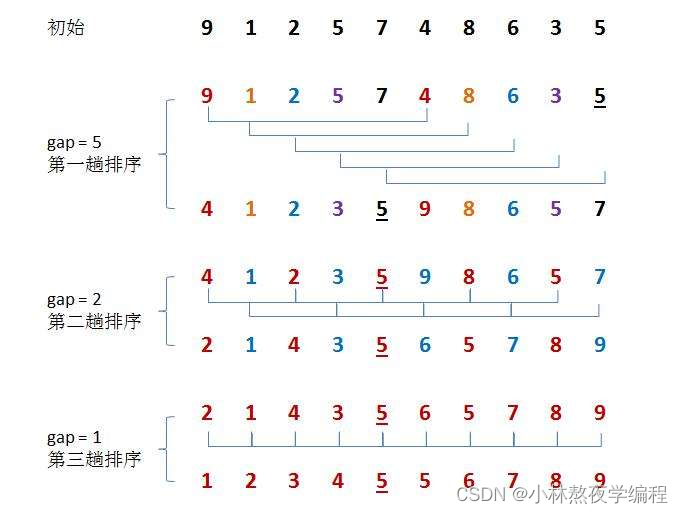
首先,增量为5,我们将数组元素分为增量(5)个子序列,每个子序列由原数组中相隔增量位置上的元素组成。所以我们有如下子序列:
然后对每个子序列进行独立的插入排序:
一趟排序之后的数组:
完成了一轮希尔排序,此时整个数组并不完全有序,但是已经比原始的数组更接近有序了。然后减小增量,通常是将原来的增量除以2(或者除以3+1),现在选择下一个增量为 2,按照此排序规则继续预排序即可,直到增量为1时,则为直接插入排序,此时则排序完成。
一个子序列排序实现:
int gap;
int end;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end-=gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
与直接插入代码不同的是,这里对end所加减的均为gap;
单次插入完成后,我们来控制单个子序列的整个过程,每实现一次排序,下一次插入的数据为end+gap。
单趟排序实现:
int gap;
for (int i = 0; i < n-gap; i += gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
这里for循环的条件为 i <n-gap 防止数组越界.
完成单个子序列的排序后,我们再对整个子序列排序:
int gap;
for (int j = 0; j < gap; j++)
{
for (int i = 0; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
外层循环(for (int j = 0; j < gap; j++))意在对每个以gap为间隔的分组进行遍历。
优化:
int gap = 3;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
这里我们将原先代码中的i += gap修改为i++,意味着这次不是按照一组一组进行了,是一次排序完每个组的第二个元素,再进行下一个元素的排序。
1.2、希尔排序代码实现
我们先对预排序的增量进行分析:
所以在实现希尔排序时,给gap固定值是行不通的。
void shellsort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;//博主写的是/3+1也可以是gap/2
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
这里无论gap是奇数还是偶数,这里gap最终都会除以到值为1。
在这里:
这里gap预排序次数还是有点多,因此我们可以再次进行修改,让gap每次除以3,为了使gap最后能回到1,我们进行加一处理。
注意:
1.3、代码测试
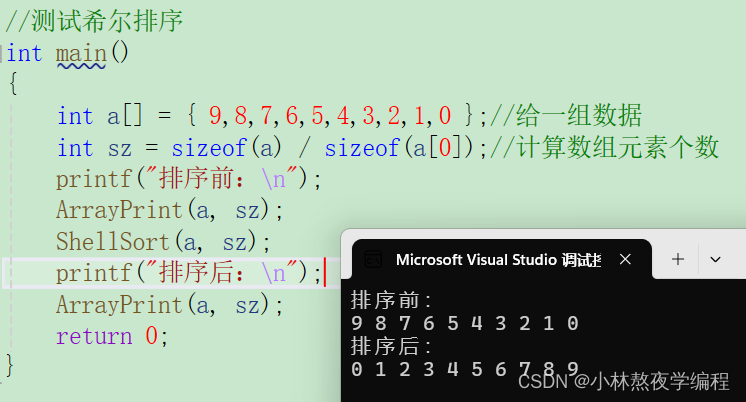
测试代码:
//测试希尔排序
int main()
{
int a[] = { 9,8,7,6,5,4,3,2,1,0 };//给一组数据
int sz = sizeof(a) / sizeof(a[0]);//计算数组元素个数
printf("排序前:\n");
arrayprint(a, sz);
shellsort(a, sz);
printf("排序后:\n");
arrayprint(a, sz);
return 0;
}测试结果:
1.4、时空复杂度分析
《数据结构(c语言版)》--- 严蔚敏

《数据结构-用面相对象方法与c++描述》--- 殷人昆
时间复杂度:
因为咋们的gap是按照knuth提出的方式取值的,而且knuth进行了大量的试验统计,我们暂时就按照:o(n^1.25) 到 o(1.6* n^1.25) 来算。
空间复杂度:
插入排序的空间复杂度为o(1),因为它是一个原地排序算法,不需要额外的存储空间来排序。
1.5、性能比较
我们在前面一弹提到了clock()函数可以获取程序启动到函数调用时之间的cpu时钟周期数,我们在这里通过具体的排序算法来进行比较性能。
注意:clock()函数的头文件是#include<time.h>,时间的单位为毫秒。
尽量使用release模式进行测试,因为release效率更高。
测试代码:
void testop()
{
srand(time(0));//随机数种子
const int n = 100000;
int* a1 = (int*)malloc(sizeof(int) * n);//动态开辟n个元素
int* a2 = (int*)malloc(sizeof(int) * n);
for (int i = 0; i < n; ++i)
{
a1[i] = rand() + i;//随机数只有3万,为了更加随机再加上i
a2[i] = a1[i];
}
//clock计算程序运行到此时的时间 毫秒
int begin1 = clock();//排序前程序运行时间
insertsort(a1, n);
int end1 = clock();//排序后程序运行时间
int begin2 = clock();
shellsort(a2, n);
int end2 = clock();
printf("insertsort:%d\n", end1 - begin1);//程勋运行时间的差值即排序运行的时间
printf("shellsort:%d\n", end2 - begin2);
free(a1);//释放空间
free(a2);
}
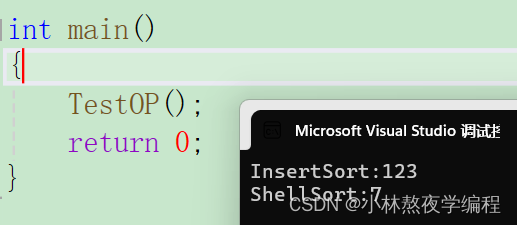
当n为10万时,release版本测试出来的结果:
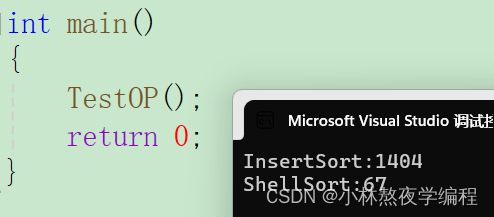
当n为100万时,release版本测试出来的结果:
希尔排序的特性总结:
总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!



发表评论