我要评论ps：本篇的主要内容就是海量数据如何进行处理，但是需要使用位图和布隆过滤器的内容。 如果没有学过位图和布隆过滤器的友友们， 自行划到文章后面有位图和布隆过滤器的模拟实现。 已经学过的友友们就可以忽略后半部分的位图和布隆的部分， 只观看前半部分的海量数据处理部分。
海量数据处理
一、已知有100亿个int数据， 现在只有1g内存， 如何在这100个int数据里面找出出现次数为2的那些数据。
解：
整形先考虑位图：100亿个int， 但是这里面隐含了一个条件， 就是整形最多只有四十二亿九千万个。 就是160亿字节。 而10亿个字节为1g。 显然， 如果将所有整形放到内存中是放不下的。 但是我们不需要储存， 只需要查找哪个数据出现次数为2， 那么就可以利用位图和布隆过滤器优化空间。 而且数据类型是int， 那么就可以使用位图——一个整形映射一个比特位。
那么， 我们就要思考， 四十亿个整形可以映射5亿个字节， 也就是500mb。同时， 我们也要思考，位图只能标记出现过或者没有出现过， 但是不能标记出现过几次。 所以要使用两个位图——位图1， 位图2。 我们都知道位图的一个比特位置为1，代表数据出现过； 一个比特位置为0， 代表数据没有出现过。
那么如果有两个位图，我们就可以让这两个比特位合起来使用。 如果位图1的对应比特位为0， 位图2的对应比特位置为1，也就是01， 代表出现一次；如果位图1的对应比特位是1， 位图2的对应比特位是0， 那么就是10， 代表出现过2次。所以两个位图一共可以统计次数最多为3.
而使用两个位图所用空间最多为1g， 空间足够。 所以可是使用两个位图的策略。 具体实现如下：
template<size_t n>
class bit_dou
{
public:
void set(size_t x)
{
if (_bit1.test(x) == false && _bit2.test(x) == false)
{
_bit1.set(x);
}
else if (_bit1.test(x) == true && _bit2.test(x) == false)
{
_bit1.reset(x);
_bit2.set(x);
}
else if (_bit1.test(x) == false && _bit2.test(x) == true)
{
_bit1.set(x);
}
}
bool test(size_t x)
{
if (_bit2.test(x) == true)
{
return true;
}
else
{
return false;
}
}
private:
bitset<n> _bit1;
bitset<n> _bit2;
};
二、给两个文件，分别有100亿个query，我们只有1g内存，如何找到两个文件交集？分别给出精确算法和近似算法。
精确策略：这里使用的是hash映射 + 统计（使用哈希map或者map） + （堆/归并/快排）
具体步骤：
假设一个query50字节， 那么100亿个query就是5000亿字节，而10亿字节是1g， 那么5000亿字节就是500g， 所以1g内存不能将这些字符串全部存下来。
这里我们使用的策略是hash + 统计（使用hashmap或者treemap） + 堆排/归并/快排，先使用hash映射将100亿个query划分到500个小文件中， 着500个小文件分别命名为a1、a2、a3……a500——这样能保证平均1个小文件里面有1g内存。
然后将另一个文件也平均分成500个小文件, 这500个小文件命名为b1、b2、b3……b500——其实两个文件可以分的再多一些， 那样就能减少一个小文件映射的query太多的概率， 导致读取文件时内存空间不足。
使用hash映射到500个小文件中， 这时候我们可以确定， 相同的query一定会被映射到同一个文件中。 并且两个大文件中如果有相同的query，那么这个query在两个大文件形成的小文件中的下标一定是相同的。 比如一个q0在第一个大文件哈希映射的文件是a122， 那么他在另一个大文件中哈希映射的文件一定是b122。
那么我们就可以利用这种性质来判断这两组小文件的交集——即a1 和b1寻找交集，寻找出来后将交集放到一个文件中（最好不要放到内存， 因为如果交集很多， 可能导致内存不够。）a2和b2寻找交集后将交集放到一个文件中……a500和b500寻找交集放到一个文件中。
要注意的是应该考虑如果划分小文件的时候， 出现单个小文件个数太大。 那么也要分情况讨论：第一种情况就是单个小文件太大，但是其中重复的元素很少， 这个时候需要将元素全部映射到map之中空间不够用， 那么就要重新使用新的哈希函数， 重新映射。另一种情况就是虽然单个小文件很大， 但是其中重复的元素很多， 可以将全部元素映射到map之中。那么就正常读取小文件即可。
上面这种做法叫做哈希切分， 就是利用分治思想： 哈希映射 + hashmap/treemap （+ 堆/归并/快排）。
近似策略：使用布隆过滤器。
近似策略就是使用布隆过滤器， 先将一个大文件中的query映射到布隆过滤器当中， 然后再将另一个大文件的数据一个一个读取， 查找是否在当前布隆过滤器之中已经出现过。 如果出现过， 就保存下来。
最后保存下来的数据， 就是两个文件的交集。
三、给两个文件，分别有100亿个整数，我们只有1g内存，如何找到两个文件交集？
这个问题和第一个问题类似，都是使用位图。 100亿个整形其实里面最多只有42亿个不同的整形， 而四十二亿个整形使用位图映射后最多只需要使用400mb， 那么我们就可以使用位图先将一个大文件的数据映射进来， 然后再对另一个文件里面的数据一个一个读取， 查看是否在当前位图映射过。如果映射过， 那么就是交集。
四、给定100亿个整数，设计算法找到只出现一次的整数？
很明显就是使用位图的一个题， 同样的使用两个位图， 建立一个能够统计次数， 最高次数是3的位图（可以叫dou_bitmap)。 那么再统计这100亿个整形， 就能统计他们的出现次数。 最后再从0开始遍历四十二亿的整数， 判断这四十二亿个整数之中哪个出现过1次。
五、给一个超过100g大小的log file, log中存着ip地址, 设计算法找到出现次数最多的ip地址？ 与上题条件相同，如何找到top k的ip？
log file明显不是整形， 那么这道题hash + 统计(hashmap/treemap) + 堆/归并/快排。
首先将100g的大文件利用hash函数切分成100个小文件。 再利用hashmap或者treemap将每个小文件中的出现最多的那个数据保存到一个文件中。 然后遍历这个文件就能找到出现次数最多的那个ip地址。
然后如何求topk的ip就要从遍历小文件的时候进行。 将每个小文件中的所有数据读到hashmap中统计其中数据出现的个数。 再利用排序将这些数据的出现个数从高到底排。 取出其中前k个ip放到一个文件之中。 所有的小文件都是上面这个操作。 最后使用一个含有k个数据的小堆。 依次遍历整个文件， 只要遇到比堆顶的数据大的， 就将数据放进堆里面。 然后弹出推顶数据， 维护堆的固定个数。最后堆中剩余的ip就是最大的k个ip。而堆顶就是topk的ip。
ps:这里总结的方法其实只有:bloomfilter/bitmap 以及 hash + 统计 + 堆/归并/快排； 另外还有几种处理海量数据的方法——外排序、多层划分、倒排索引等等。 这些博主知识储备不足， 在这里不好讲解， 有兴趣的友友可以按照自己的兴趣以及能力自行学习。
位图
学习位图之前首先要知道的一点就是位图， 布隆过滤器都是利用了哈希的思想。解决的是内存不够的问题。 就是说， 它们可以处理的数据更多。 更能节省空间。 但是也并不是只有优点，位图存在只能处理整形数据的问题。 而布隆过滤器存在不准确的问题。接下来实现位图：
一般的哈希表像哈希桶， 闭散列。 都是利用一块空间来映射数据，同时需要开空间储存数据。如图位哈希桶图：
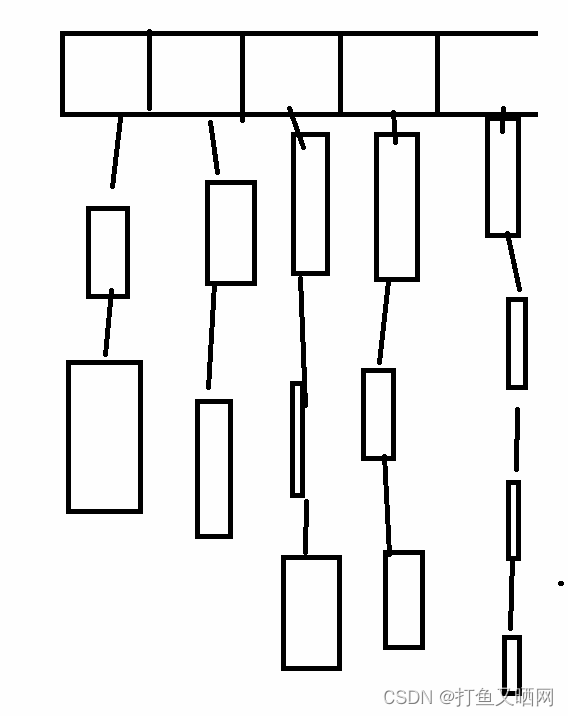
但是位图是利用一个比特位来映射数据，只用来映射， 不进行存储。如果改位置映射过， 就置为1（下图中的红代表1）， 没映射过就是0（下图无色， 即默认值）。
//类的定义（要用模板size_t, 因为要指定位图的大小， 参数是几， 说明至少有多少数据， 就要保证最少开几个比特位空间。）
template<size_t n> //模板使用来规定创建的位图大小。 n是几， 就保证最少有几个比特位。
class bitset
{
};//使用整形数组来模拟一块连续的空间
template<size_t n>
class bitset
{
bitset()
{
//这里要保证开的空间足够， 但是n / 32会消除小数点，开的空间要小于等于需求。 所以要多开一个整形空间。
_bits.resize(n / 32 + 1);
}
private:
vector<int> _bits; //使用整型数组来模拟一块连续的空间。
};//进行映射时， 如何定位第几个比特位
一个整形时4个字节， 32个比特位， 假设当前数据位x。 那么x / 32就是当前需要映射的第几个整形。而x % 32就是当前要映射的这个整形的第几个比特位。
当进行定位比特位时， 我们就可以这样写:
int i = x / 32; //要映射的第几个整形
int j = x % 32; //要映射的第几个整形的第几个比特位。
//将当前比特位标记为1， 如何不修改其他比特位， 只将当前比特位置为1.
标记比特位要使用按位操作。 而按位操作分为按位与‘&’， 按位或'|', 按位异或'^'。 其中‘&’的规则是：有0就是0， 全1才是1； '|'的规则是：有1就是1， 全0才是0； '^'的规则是：相同为0， 相异为1。
这里可以使用'|‘操作， 先将1向高位移动 j 个位置。再让第 i 个整形按位或上1移动后的数。 就是想要的结果， 如图:
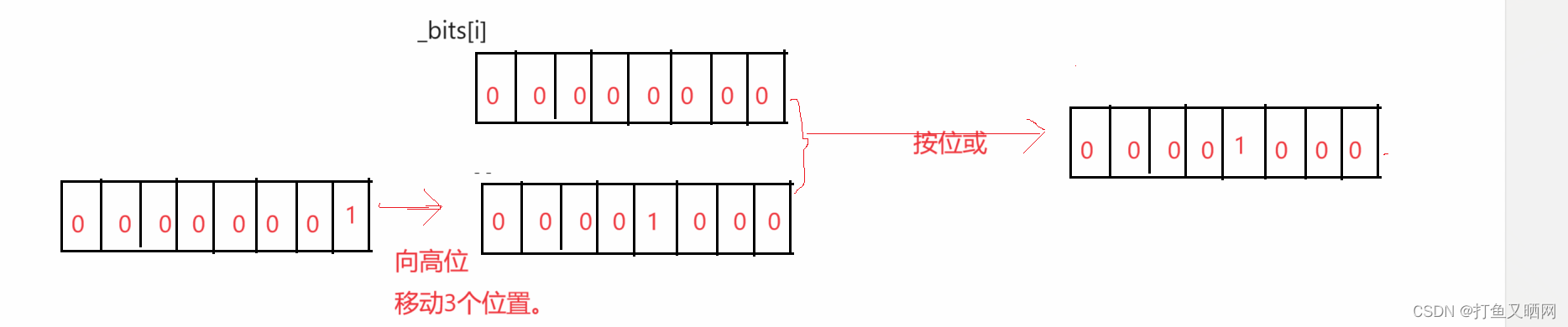
转化为代码就是如下， 这也是第一个接口（位图有三个接口， set, reset, test。该接口是set).
template<size_t n>
class bitset
{
public:
bitset()
{
//这里要保证开的空间足够， 但是n / 32会消除小数点，开的空间要小于等于需求。 所以要多开一个整形空间。
_bits.resize(n / 32 + 1);
}
void set(int x)
{
int i = x / 32; //要映射的第几个整形
int j = x % 32; //要映射的第几个整形的第几个比特位。
_bits[i] |= (1 << j); //按位或：有1就是1， 全0才是0.
}
private:
vector<int> _bits; //使用整型数组来模拟一块连续的空间。
};//消除某一个比特位的映射（reset接口)
消除某一个位置的映射需要只将某一个比特位置为0， 其他的位置不变。如果是或操作， 就要让其他位置都是0， 但是并不能消除特定位置的1. 所以就要使用与操作， 让其他位置都是1， 特定位置都是0. 就能让特定位置由1变成0. 而其他位置与上1还是它本身, 代码如下:
template<size_t n>
class bitset
{
public:
bitset()
{
//这里要保证开的空间足够， 但是n / 32会消除小数点，开的空间要小于等于需求。 所以要多开一个整形空间。
_bits.resize(n / 32 + 1);
}
void set(int x)
{
int i = x / 32; //要映射的第几个整形
int j = x % 32; //要映射的第几个整形的第几个比特位。
_bits[i] |= (1 << j); //按位或：有1就是1， 全0才是0.
}
void reset(int x)
{
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}
private:
vector<int> _bits; //使用整型数组来模拟一块连续的空间。
};//测试某一个数据有没有被映射过， 其实就是看某一个比特位有没有被映射过（test)
测试某一个位置有没有被映射过， 只需要让该位置与上1， 其他位置遇上0即可。 当其他位置与上0， 那么都变成0， 特定位置与上1， 如果这个位置原本是1， 那么结果就是1。 非0就是真， 如果该位置原本是0， 与上0之后也是零， 其他位置也是零。 所以结果就是0， 0为假。 代码如下:
template<size_t n>
class bitset
{
public:
bitset()
{
//这里要保证开的空间足够， 但是n / 32会消除小数点，开的空间要小于等于需求。 所以要多开一个整形空间。
_bits.resize((n / 32) + 1, 0);
}
void set(int x)
{
int i = x / 32; //要映射的第几个整形
int j = x % 32; //要映射的第几个整形的第几个比特位。
_bits[i] |= (1 << j); //按位或：有1就是1， 全0才是0.
}
void reset(int x)
{
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}
bool test(int x)
{
int i = x / 32;
int j = x % 32;
return _bits[i] &= (1 << j);
}
private:
vector<int> _bits; //使用整型数组来模拟一块连续的空间。
};
布隆过滤器
位图只能用来处理整形， 而布隆过滤器可以用来处理字符串。 弥补了位图只能用来处理整形的缺点。 但是因为字符串的个数太多，（首先长度不确定， ascii码中的字符就有128个。 如果是10位长， 就是128^10） 如果一个字符串可以利用哈希函数转化为一个整形，而字符串的个数远远超过了整形的个数（整型只有四十二亿九千万个）。那么根据鸽巢原理， 就一定会有两个不同的字符串被转化成了相同的整数。 这个时候结果就不准了， 所以布隆过滤器就使用了多个哈希函数， 将一个字符串来映射多个位置。 如图:
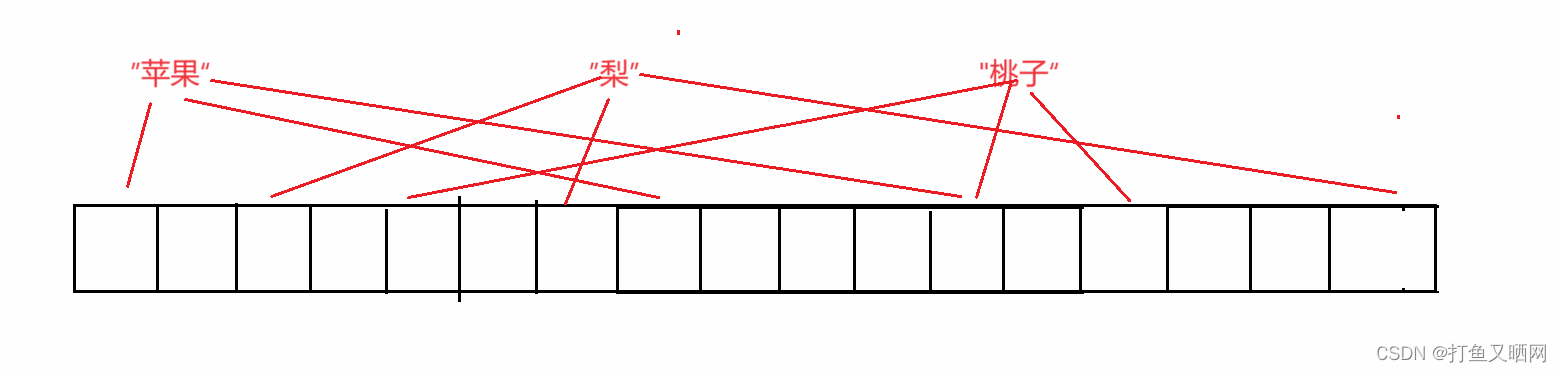
图中有三个字符串——苹果、梨、桃子。 同时每个字符串都有三个映射的位置， 并且苹果和桃子有一个哈希映射的位置相同。 如果这个时候再来一个西瓜， 我们要查找一下西瓜存在不存在。
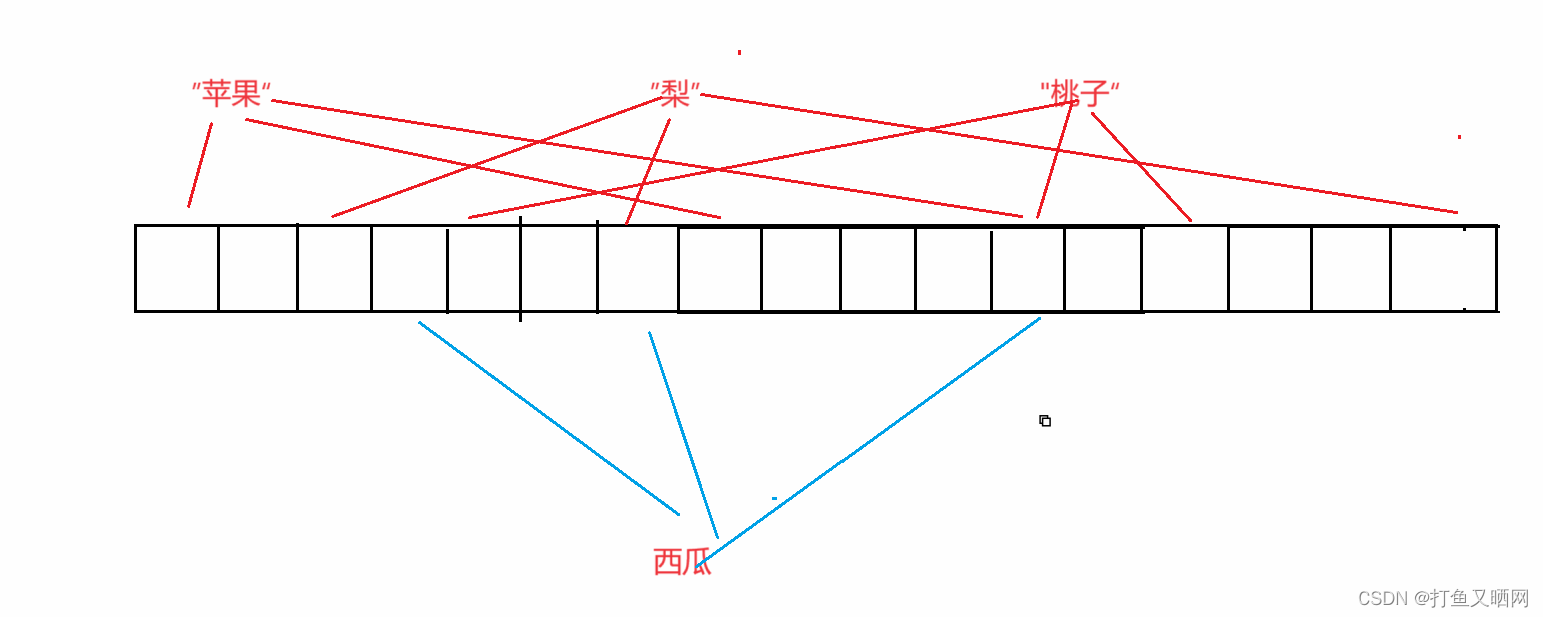如图， 虽然西瓜有两个哈希函数映射的位置都被标记过了， 但是最左边那个映射的位置没有被标记过， 那么这样就可以看作西瓜没有出现过。 因为如果西瓜出现过。 这三个位置应该都被映射过， 但是现在这三个位置中有一个没有被映射过。 所以说明其他两个位置应该是和其他字符串发生了哈希冲突导致的, 西瓜就没有被映射过——现在， 这种没有被映射过的情况是一定的， 只要判断出一个字符串没有被映射过， 那么结果就是准确的。即：布隆过滤器的没有出现过是准确的。
那么， 如果西瓜的映射位置不是上面那样了， 变成下图:
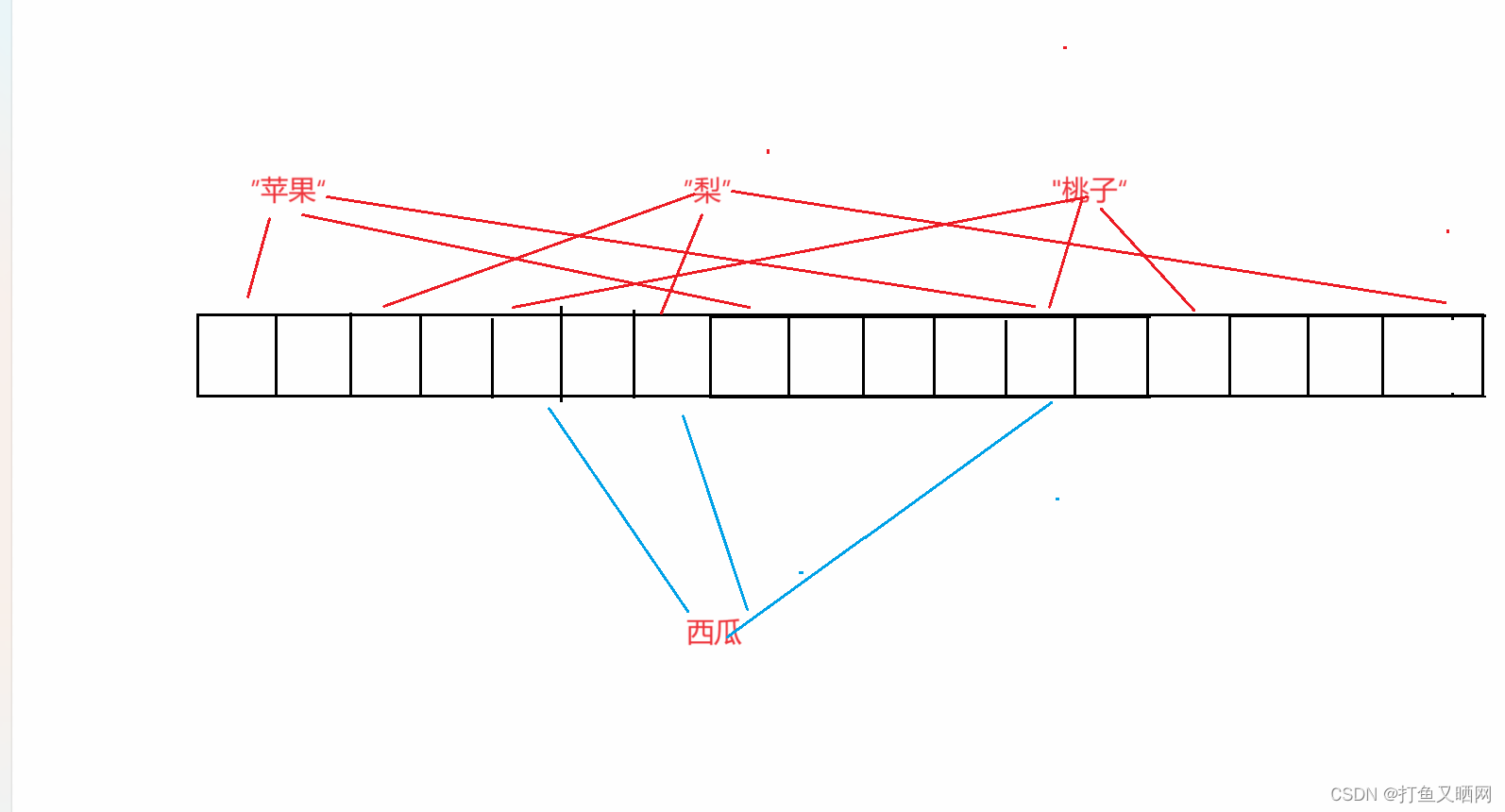
现在， 这三个位置都发生了哈希冲突， 返回的结果告诉我们西瓜出现过。 但是其实习惯并没有出现过， 这就说明如果判断一个字符串， 结果是出现过。 那么结果就是不准确的——现在， 这种被映射过的情况是不准确的。 即：布隆过滤器的出现过是不准确的。
要提升布隆过滤器判断出现过的准确性， 就要增加哈希函数。 从图中我们可以看出来， 如果一个字符串映射的位置越多，那么就越难发生所有位置都冲突的情况。 但是， 另一个需要注意的是， 如果我们的字符串映射的位置太多了， 可能导致空间内大部分空间都被映射过。 那么哈希冲突的概率也会提升， 所以还是不行， 那么就要增加空间。 这就导致了一个问题——如果要提高布隆过滤器判断出现过的准确性， 就要增加哈希函数。 而增加哈希函数， 就要消耗更多的空间。
下面是布隆过滤器的准确性和哈希函数的个数的关系图：
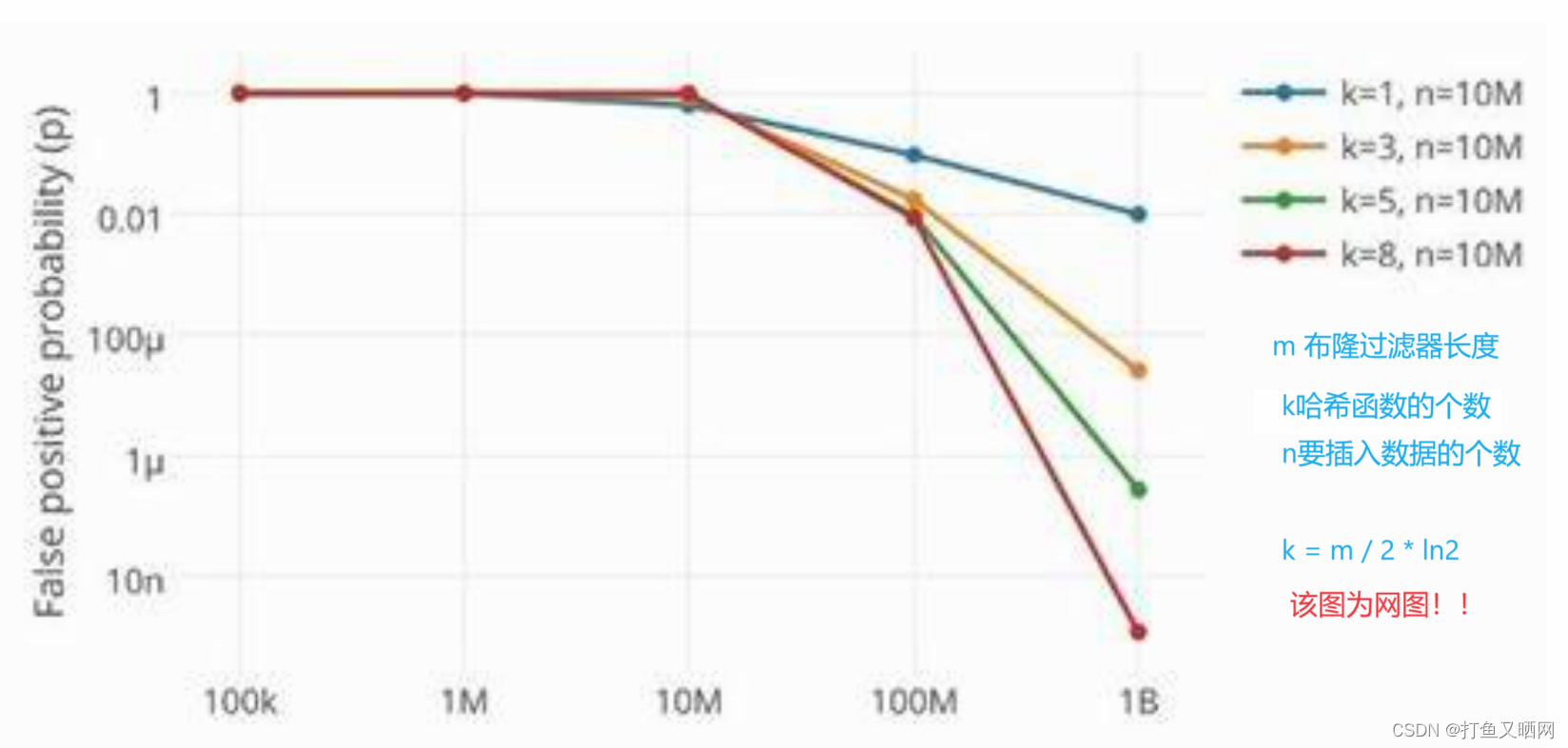
布隆过滤器可以用来处理字符串， 以及其他类型。 只要使用相应的哈希函数即可。 这里使用三个哈希函数来封装布隆过滤器——三个哈希函数分别是：bkdr哈希， djb哈希， ap哈希
//模版参数有五个， 一个要处理的数据个数， 一个要处理的数据类型， 三个哈希函数。 如图:
template<size_t n, class type = string, class hf1 = bkdrhash<type>, class hf2 = djbhash<type>, class hf3 = aphash<type>>
class bloomfilter
{
};//三个哈希函数（都可以在网上找到， 这里贴上方便友友使用）
三个哈希函数， 都要有一个关于字符串类型的特化形式。 因为我们使用布隆过滤器使用的最多的就是字符串类类型。 要实现字符串类型的特化就是使用模板的特化机制。如下代码:
//一般先创建一个模板类
template<class t>
class _class
{};
//然后在该模板类后面再跟一模板类，但是这个类里面没有参数， 类名后面跟参数。
template<>//没参数
class _class<string>//类名后跟string
{};
bkdr函数的定义是这样的
//第一个带参数的自行进行修改
template<class type>
struct bkdrhash
{
int operator()(const type& key)
{
return key;
}
};
//字符串处理的特化
template<>
struct bkdrhash<string>
{
int operator()(const string& str)
{
int hash = 0;
for (auto& e : str)
{
hash *= 31;
hash += e;
}
return hash;
}
};djb哈希的定义如下：
// //第一个带参数的自行进行修改
template<class type>
struct djbhash
{
int operator()(const type& key)
{
return key;
}
};
template<>
struct djbhash<string>
{
int operator()(const string& str)
{
int hash = 0;
for (auto& e : str)
{
hash += (hash << 5) + e;
}
hash = hash & ~(hash << 31);
return hash;
}
};
aphash
template<class type>
struct aphash
{
int operator()(const type& x)
{
return x;
}
};
template<>
struct aphash<string>
{
int operator()(const string& str)
{
int hash = 0;
for (int i = 0; i < str.size(); i++)
{
if (i & 1 == 0)
{
hash ^= ((hash << 7) ^ str[i] ^ (hash >> 3));
}
else
{
hash ^= ((hash << 11) ^ str[i] ^ (hash >> 5));
}
}
return hash;
}
};
//布隆过滤器也是一个比特位，一个比特位进行映射。所以底层可以使用位图， 如下：
template<size_t n, class type = string, class hf1 = bkdrhash<type>, class hf2 = djbhash<type>, class hf3 = aphash<type>>
class bloomfilter
{
public:
//不需要构造函数
private:
bitset<n> _bits;
};//布隆过滤器的接口——set（建立映射关系）、test（查看该数据是否存在， 存在不准确， 不存在准确）
template<size_t n, class type = string, class hf1 = bkdrhash<type>, class hf2 = djbhash<type>, class hf3 = aphash<type>>
class bloomfilter
{
public:
//不需要构造函数, 自动调用位图的构造函数
//set就是利用三个哈希函数， 分别在位图上面映射一次。
void set(type x)
{
int hash1 = hf1()(x);
int hash2 = hf2()(x);
int hash3 = hf3()(x);
_bits.set(hash1);
_bits.set(hash2);
_bits.set(hash3);
}
bool test(type x)
{
int hash1 = hf1()(x);
int hash2 = hf2()(x);
int hash3 = hf3()(x);
//只有当三个位置都是映射过的， 这个数据才可能被映射过。但只要有一个没有映射过， 那么这个数据就一定没有映射过
if (_bits.test(hash1) && _bits.test(hash2) && _bits.test(hash3)) return true;
return false;
}
private:
bitset<n> _bits;
};以上， 就是海量数据处理方面相关的知识点。
发表评论