目录
一、引言
堆排序的简介
堆排序的特点
二、堆的概念
三、堆排序算法的原理
四、堆排序的步骤
🍃构建堆
这里分别给出向下调整建小堆和向下调整建大堆的算法
(如果关于向上调整算法和向下调整算法有疑惑,建议了解完堆的这篇文章之后再来看
【数据结构与算法】探索数组在堆数据结构中的妙用:从原理到实现-csdn博客)
void adjustdownsmall(datatype* a, int parent, int size)//向下调整建小堆算法
{
int child = parent * 2 + 1;//先假定左孩子小
while (child < size)//循环条件是未调整至叶子节点
{
if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小,改变为右孩子
child++;
if (a[child] < a[parent])//如果子节点小于父节点,交换位置
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void adjustdownbig(datatype* a, int parent, int size)//向下调整建大堆算法
{
int child = parent * 2 + 1;//先假定左孩子大
while (child < size)//循环条件是未调整至叶子节点
{
if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大,改变为右孩子
child++;
if (a[child] > a[parent])//如果子节点大于父节点,交换位置
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
🍃交换与调整
swap(&a[0], &a[end]);//交换堆顶和堆尾数据
end--;
adjustdownsmall(a, 0, end);//向下调整恢复堆的结构 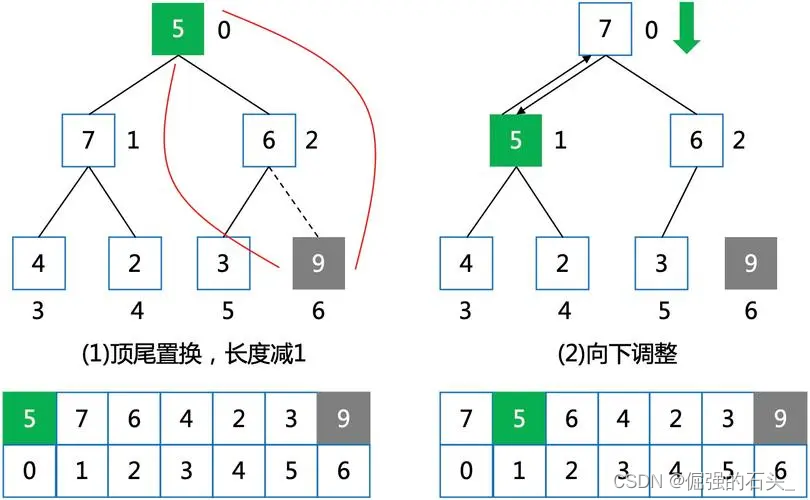
🍃重复过程
五、堆排序的性能分析
🍃时间复杂度:
🍃空间复杂度:
六、示例代码
(分别给出了完整的降序排序算法和升序排序算法)
#include<stdio.h>
#include<stdlib.h>
#if 1
//堆排序
typedef int datatype;
void swap(datatype* a, datatype* b)
{
datatype tmp = *a;
*a = *b;
*b = tmp;
}
void adjustdownsmall(datatype* a, int parent, int size)//向下调整建小堆算法
{
int child = parent * 2 + 1;//先假定左孩子小
while (child < size)//循环条件是未调整至叶子节点
{
if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小,改变为右孩子
child++;
if (a[child] < a[parent])//如果子节点小于父节点,交换位置
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void adjustdownbig(datatype* a, int parent, int size)//向下调整建大堆算法
{
int child = parent * 2 + 1;//先假定左孩子大
while (child < size)//循环条件是未调整至叶子节点
{
if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大,改变为右孩子
child++;
if (a[child] > a[parent])//如果子节点大于父节点,交换位置
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void heapsortdorder(datatype* a,int size)//降序排序
{
//向下调整建小堆
for (int i = (size - 2) / 2; i >= 0; i--)//从最后一个父节点调整
{
adjustdownsmall(a, i, size);
}
int end = size - 1;
while (end>0)
{
swap(&a[0], &a[end]);//交换堆顶和堆尾数据
end--;
adjustdownsmall(a, 0, end);//向下调整恢复堆的结构
}
}
void heapsortaorder(datatype* a, int size)//升序排序
{
//向下调整建大堆
for (int i = (size - 2) / 2; i >= 0; i--)//从最后一个父节点调整
{
adjustdownbig(a, i, size);
}
int end = size - 1;
while (end > 0)
{
swap(&a[0], &a[end]);//交换堆顶和堆尾数据
end--;
adjustdownbig(a, 0, end);//向下调整恢复堆的结构
}
}
#endif
void print(datatype* a, int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 12,3,5,78,46,15,23,19,20,36,52 };
int size = sizeof(arr) / sizeof(arr[0]);
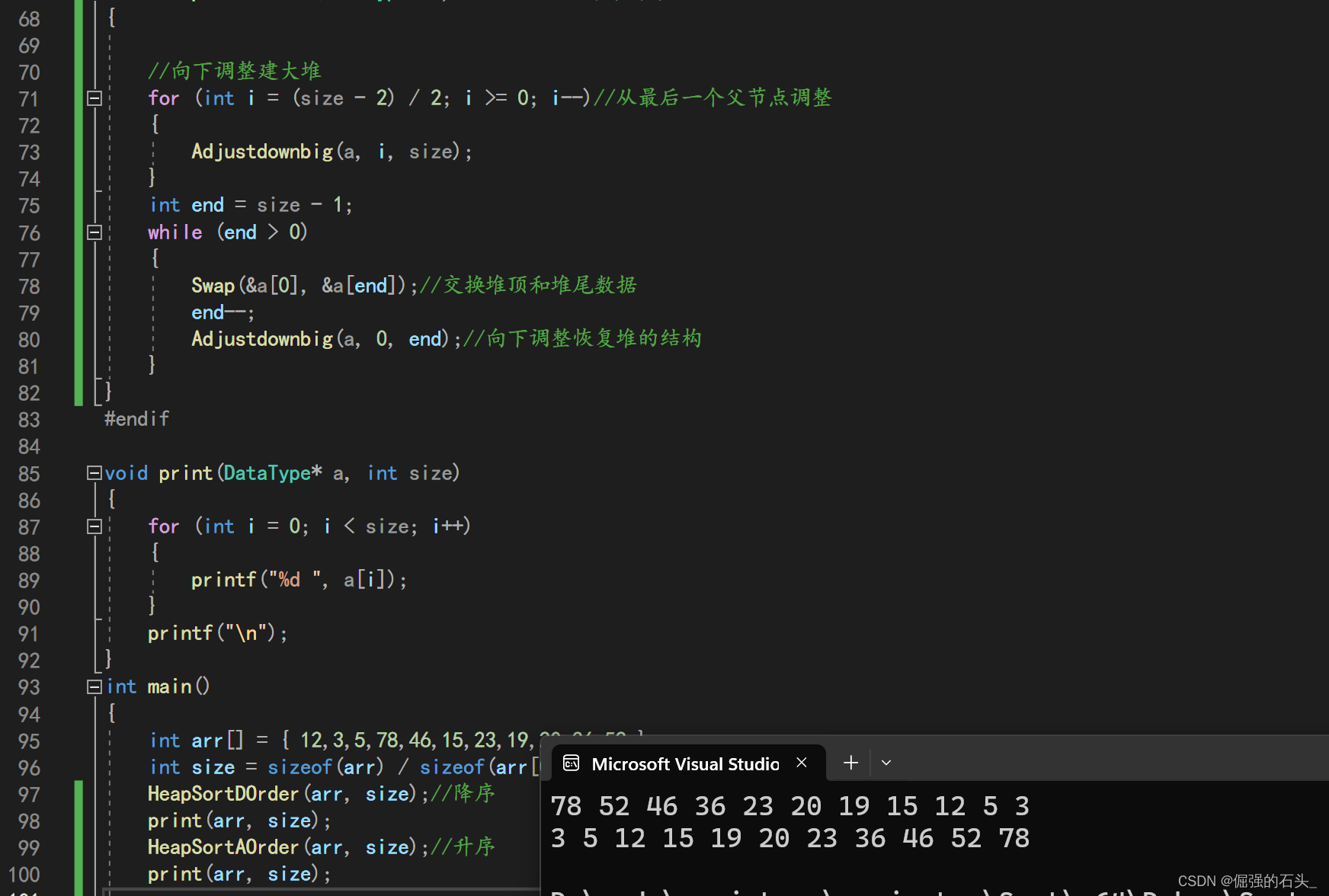
heapsortdorder(arr, size);//降序
print(arr, size);
heapsortaorder(arr, size);//升序
print(arr, size);
} 
七、总结



发表评论