我要评论目录
一.引言
决策树（decision tree）是一种分类和回归方法，是基于各种情况发生的所需条件构成决策树，以实现期望最大化的一种图解法。本文将介绍决策树和决策树实战案例。
二.决策树
2.1 决策树定义
决策树可以认为是 if-then 规则的集合，也可以认为时定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性，分类速度快。如何得到该决策树叫做决策树学习，决策树学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测试，对新的数据，利用决策树模型进行分类。
2.1.1 决策树的组成
决策树由结点和有向边组成。结点有两种类型：内部结点（圆）和叶结点（矩形）。其中，内部结点表示一个特征（属性）；叶结点表示一个类别。而有向边则对应其所属内部结点的可选项（属性的取值范围），如图1所示。
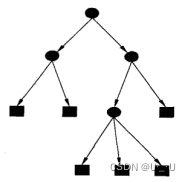
图 1
用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点，最后将实例分到叶节点的类中。
2.1.2 决策树的构建
决策树的本质是从训练集中归纳出一套分类规则，使其尽量符合以下要求：
如果按照某个特征对数据进行划分时，它能最大程度地将原本混乱的结果尽可能划分为几个有序的大类，则就应该先以这个特征为决策树中的根结点。接着，不断重复这一过程，直到整棵决策树被构建完成为止。因此引入信息熵，熵（entropy)是表示随机变量不确定性的度量，即是物体内部的混乱程度。构建决策树的实质是对特征进行层次选择，而衡量特征选择的合理性指标，则是熵。
熵公式：
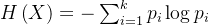
当某个集合含有多个类别时，此时 𝑘 较大， 𝑝𝑖 的数量过多；且整体的 𝑝𝑖 都会因 𝑘 的过大而普遍较小，从而使得 𝐻(x) 的值过大。这正好符合“熵值越大，事物越混乱”的定义。
2.1.3 条件熵的引入
根据熵的定义，在构建决策树时我们可采用一种很简单的思路来进行“熵减”：每当要选出一个内部结点时，考虑样本中的所有“尚未被使用”特征，并基于该特征的取值对样本数据进行划分。既有条件熵，条件熵 𝐻(𝑌 | 𝑋) 表示在已知随机变量 𝑋 的条件下随机变量 𝑌 的不确定性。
条件熵公式：
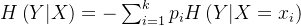
2.2 决策树的划分选择
决策树学习的关键在于：如何选择最优划分属性。一般而言，随着划分过程的不断进行，我们自然希望决策树各分支结点所包含的样本尽可能属于同一类别，特征选择是决策树构建的关键的一步，它决定了使用哪个属性来划分数据集。我们常用的特征选择方法包括信息增益、增益率和基尼指数
2.2.1 信息增益（id3使用的划分方式）
划分数据集的大原则是：将无序数据变得更加有序，但是各种方法都有各自的优缺点，信息论是量化处理信息的分支科学，在划分数据集前后信息发生的变化称为信息增益，获得信息增益最高的特征就是最好的选择，所以必须先学习如何计算信息增益。
信息增益表示某特征 𝑋 使得数据集 𝐷 的不确定性减少程度，定义为集合 𝐷 的熵与在给定特征 𝑋 的条件下 𝐷 的条件熵 𝐻(𝐷 | 𝑋) 之差，即
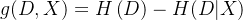
从该式可以看出，信息增益表达了样本数据在被分类后的专一性。因此，它可以作为选择当前最优特征的一个指标。信息增益越大，说明划分所获得的“纯度提升”越大。
2.2.2 信息增益率（ c4.5 算法选用的评估标准）
以信息增益作为划分数据集的特征时，其偏向于选择取值较多的特征。c4.5是id3的改进版本，它使用信息增益比来选择最优的属性，同时支持处理连续型属性和缺失值。信息增益率 𝑔𝑅(𝐷, 𝑋) 定义为其信息增益 𝑔(𝐷, 𝑋) 与数据集 𝐷 在特征 𝑋 上值的熵 𝐻x(𝐷) 之比，其计算方式如下：
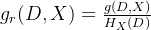
其中，hx(d) = - σ (|di| / |d|) * log2(|di| / |d|)，称为数据集d关于x的取值熵。从上式可以看出，信息增益率考虑了特征本身的熵（此时，当某特征取值类别较多时，𝑔𝑅(𝐷, 𝑋) 式中的分母也会增大），从而降低了 “偏向取值较多的特征” 这一影响。信息增益率能明显降低取值较多的特征偏好现象，从而更合理地评估各特征在划分数据集时取得的效果。
2.2.3 基尼指数 （ cart算法选用的评估标准）
分类回归树（classification and regression tree，cart）便是答案，它通过使用基尼系数来代替信息增益率，从而避免复杂的对数运算。基尼指数用于度量数据集的不纯度。基尼指数越小，说明数据集的纯度越高。分类问题中，假设有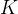
个类，样本点属于
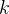的概率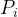
，则概率分布的基尼指数：
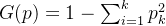
对给定的样本集合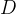
，基尼指数：
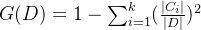
cart决策树使用“基尼指数”来选择划分属性。数据集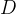的纯度可用基尼值来度量，
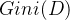越小，则数据集的纯度越高。cart生成的是二叉树，计算量相对来说不是很大，可以处理连续和离散变量，能够对缺失值进行处理。
2.3 决策树的剪枝
剪枝：顾名思义就是给决策树 "去掉" 一些判断分支，同时在剩下的树结构下仍然能得到不错的结果。之所以进行剪枝，是为了防止或减少 "过拟合现象" 的发生，是决策树具有更好的泛化能力。具体做法：去掉过于细分的叶节点，使其回退到父节点，甚至更高的节点，然后将父节点或更高的叶节点改为新的叶节点。
剪枝的两种方法：
注意：决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。
三.实战案例
3.1 导入所需的python库和鸢尾花数据集
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.tree import decisiontreeclassifier
iris = load_iris()
# 选用鸢尾花数据集的特征
# 尾花数据集的 4 个特征分别为：sepal length:、sepal width、petal length:、petal width
# 下面选用 petal length、petal width 作为实验用的特征
x= iris.data[:,2:]
# 取出标签
y = iris.target
# 设置决策树的最大深度为 2（也可以限制其他属性）
tree_clf = decisiontreeclassifier(max_depth = 2)
# 训练分类器
tree_clf.fit(x, y)
3.2 决策树进行可视化展示
# 导入对决策树进行可视化展示的相关包
from sklearn.tree import export_graphviz
export_graphviz(
# 传入构建好的决策树模型
tree_clf,
# 设置输出文件（需要设置为 .dot 文件，之后再转换为 jpg 或 png 文件）
out_file="iris_tree.dot",
# 设置特征的名称
feature_names=iris.feature_names[2:],
# 设置不同分类的名称（标签）
class_names=iris.target_names,
rounded = true,
filled = true
)
# 该代码执行完毕后，此 .ipython 文件存放路径下将生成一个 .dot 文件（名字由 out_file 设置，此处我设置的文件名为 iris_tree.dot）
结果
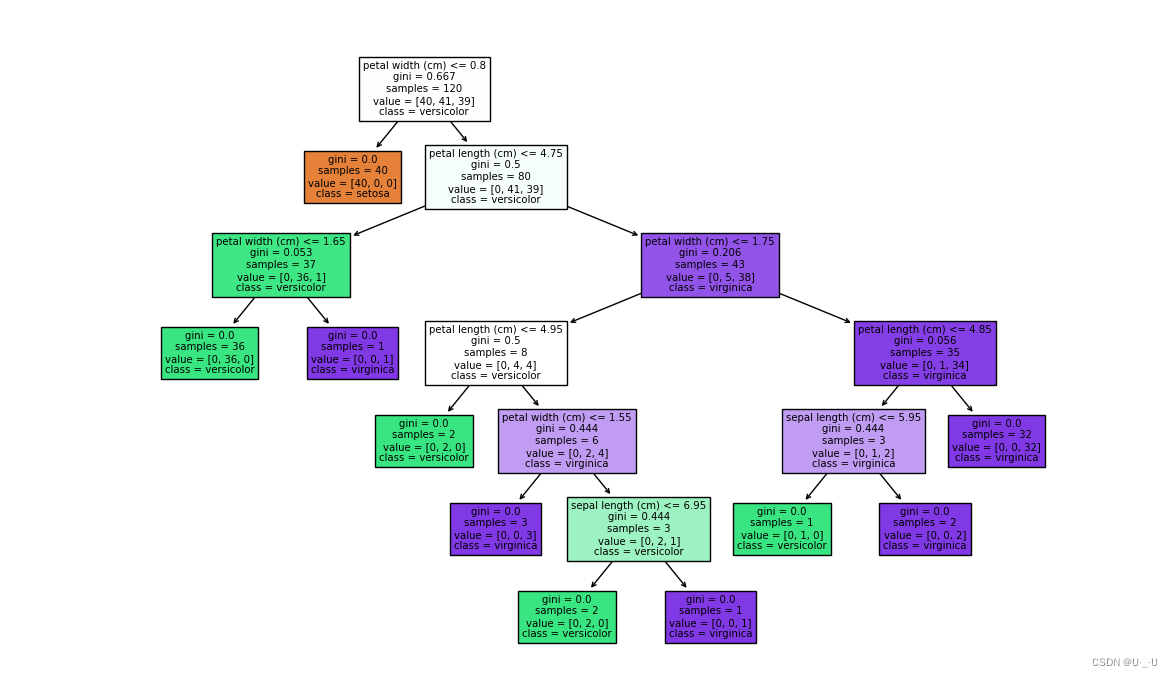
图 2
3.3 概率估计
定义绘制决策边界的函数：
from matplotlib.colors import listedcolormap
# 定义绘制决策边界的函数
def plot_decision_boundary(clf,x, y, axes=[0,7,0,3], iris=true,legend=false,plot_training=true):
# 构建坐标棋盘
# 等距选 100 个居于 axes[0],axes[1] 之间的点
x1s = np.linspace(axes[0],axes[1],100)
# x1s.shape = (100,)
# 等距选 100 个居于 axes[2],axes[3] 之间的点
x2s = np.linspace (axes[2],axes[3],100)
# x2s.shape = (100,)
# 构建棋盘数据
x1,x2 = np.meshgrid(x1s,x2s)
# x1.shape = x2.shape = (100,100)
# 将构建好的两个棋盘数据分别作为一个坐标轴上的数据（从而构成新的测试数据）
# x1.ravel() 将拉平数据（得到的是个列向量（矩阵）），此时 x1.shape = (10000,)
# 将 x1 和 x2 拉平后分别作为两条坐标轴
# 这里用到 numpy.c_() 函数，以将两个矩阵合并为一个矩阵
x_new = np.c_[x1.ravel(),x2.ravel()]
# 此时 x_new.shape = (10000,2)
# 对构建好的新测试数据进行预测
y_pred = clf.predict(x_new).reshape(x1.shape)
# 选用背景颜色
custom_cmap = listedcolormap(['#fafab0', '#9898ff', '#a0faa0'])
# 执行填充
plt.contourf(x1,x2,y_pred,alpha=0.3,cmap=custom_cmap)
if not iris:
custom_cmap2 = listedcolormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1,x2, y_pred,cmap=custom_cmap2,alpha=0.8)
if plot_training:
plt.plot(x[:,0][y==0],x[:,1][y==0],"yo", label="iris-setosa")
plt.plot(x[:,0][y==1],x[:,1][y==1],"bs", label="iris-versicolor")
plt.plot(x[:,0][y==2],x[:,1][y==2],"g^", label="iris-virginica")
plt.axis(axes)
if iris:
plt.xlabel("petal length", fontsize=14)
plt.ylabel("petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel (r"$x_2$", fontsize=18,rotation = 0)
if legend:
plt.legend(loc="lower right", fontsize=14)
绘制决策边界：
# 绘制决策边界
plt.figure(figsize=(8,4))
plot_decision_boundary(tree_clf, x, y)
# 为了便于理解，这里还绘制了决策边界的切割线（基于前面得到的图片）
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75,1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
# 绘制决策边界划分出的类别所处深度
plt.text(1, 1.0, "depth=1", fontsize=15)
plt.text(3.2, 2, "depth=2", fontsize=13)
plt.text(3.2,0.5, "depth=2", fontsize=13)
plt.title('decision tree decision boundaries')
plt.show()
结果：
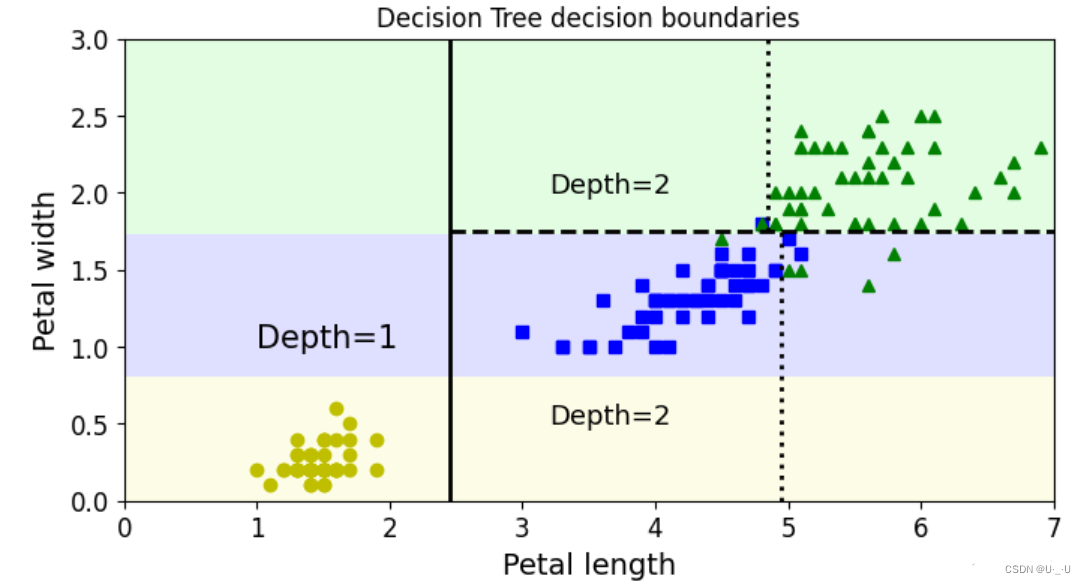
图 3
四.总结
4.1 决策树优缺点
优点：
缺点：
4.2 结语
决策树作为一种简单而有效的机器学习算法，在实际应用中发挥着重要作用。通过深入理解决策树的原理和算法，我们可以更好地利用它来解决实际问题，并且不断改进和优化模型。
发表评论