
文章目录
散列表(也称哈希表): 根据关键字而直接进行访问的数据结构。也就是说,散列表建立了关键字和存储地址之间的一种直接映射关系。
散列函数(也称哈希函数): 一个把查找表中的关键字映射成该关键字对应的地址的函数,记为 hash(key)=addr(这里的地址可以是数组下标、索引或内存地址等)。散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为冲突,这些发生冲突的不同关键字称为同义词。一方面,设计得好的散列函数应尽量减少这样的冲突;另一方面,由于这样的冲突总是不可避免的,所以还要设计好处理冲突的方法。
一、散列函数构造
(一)直接定址法
直接取关键字的某个线性函数值为散列地址,散列函数为:h(key)=key或 h(key)=a×key+b
其中a和b是常数。这种方法计算最简单,且不会产生冲突。它适合关键字的分布基本连续的情况,若关键字分布不连续,空位较多,则会造成存储空间的浪费。
(二)除留余数法
这是一种最简单、最常用的方法,假定散列表表长为m,取一个不大于m但最接近或等于m的质数 p,利用以下公式把关键字转换成散列地址。散列函数为:h(key)=key%p
除留余数法的关键是选好 p,使得每个关键字通过该函数转换后等概率地映射到散列空间上的任意一个地址,从而尽可能减少冲突的可能性。
(三)数字分析法
设关键字是r进制数(如十进制数),而r个数码在各位上出现的频率不一定相同,可能在某些位上分布均匀一些,每种数码出现的机会均等;而在某些位上分布不均匀,只有某几种数码经常出现,此时应选取数码分布较为均匀的若干位作为散列地址。这种方法适合于已知的关键字集合,若更换了关键字,则需要重新构造新的散列函数。
(四)平方取中法
取关键字的平方值的中间几位作为散列地址。具体取多少位要视实际情况而定。这种方法得到的散列地址与关键字的每位都有关系,因此使得散列地址分布比较均匀,适用于关键字的每位取值都不够均匀或均小于散列地址所需的位数。
二、解决冲突方法
(一)开放定址法
所谓开放定址法,是指表中可存放新表项的空闲地址既向它的同义词表项开放,又向它的非同义词表项开放。递推公式为:hi=(h(key)+di)%m。其中h(key)为散列函数;i=1,2,⋯,k(k≤m-1);m表示散列表表长;di为增量序列。
主要有以下几种方法。
1.线性探测法
冲突发生时,依次向后寻找空位,di=1,2,⋯,m-1。。会造成大量元素在相邻的散列地址上聚集起来,大大降低了查找效率。
2.平方探测法
也称二次探测法。di=12,-12,22,-22,⋯,k2,-k2,其中k≤m/2,散列表长度m必须是一个可以表示成4k+3的素数。平方探测法是一种处理冲突的较好方法,可以避免出现聚集问题,它的缺点是不能探测到散列表上的所有单元,但至少能探测到一半单元。
3.双散列法
di = i x hash2(key)。需要使用两个散列函数,当通过第一个散列函数 h(key)得到的地址发生冲突时,则利用第二个散列函数 hash?(key)计算该关键字的地址增量。它的具体散列函数形式如下:h=(h(key)+i x hash2(key))%m,初始探测位置hi=h(key)%m,i是冲突的次数,初始为0。
4.伪随机序列法
di=伪随机数序列。
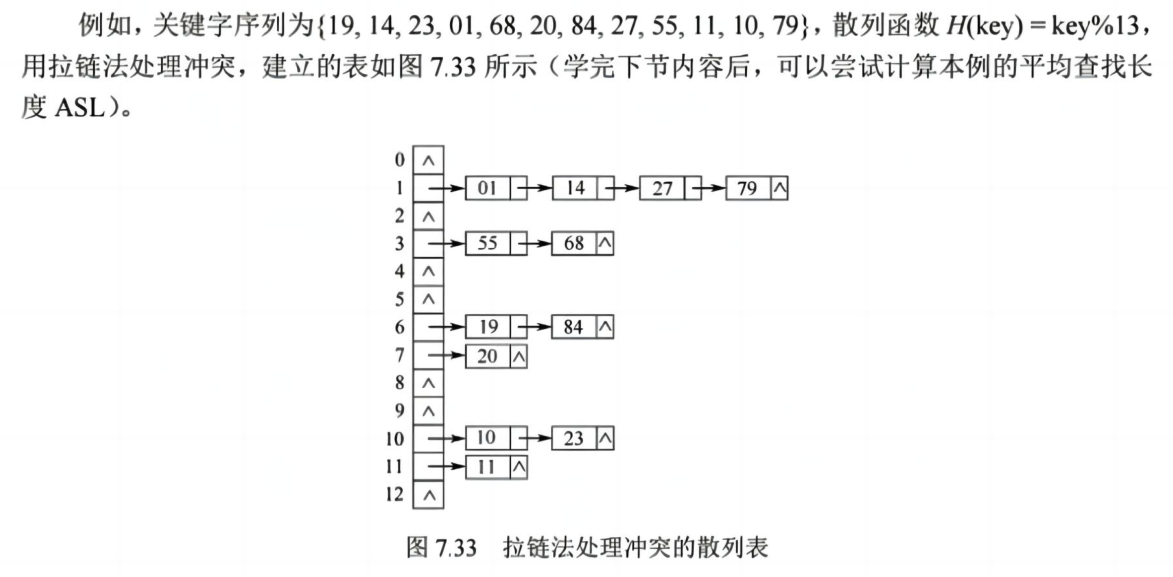
(二)拉链法
为了避免非同义词发生冲突,可以把所有的同义词存储在一个线性链表中,这个线性链表由其散列地址唯一标识。拉链法适用于经常进行插入和删除的情况。
三、查找效率分析
散列表的查找效率取决于三个因素:散列函数、处理冲突的方法和装填因子。散列表的装填因子一般记为α,定义为一个表的装满程度。
对同一组关键字,设定相同的散列函数,则不同的处理冲突的方法得到的散列表不同,它们的平均查找长度也不同,应能在给出散列表的长度、元素个数及散列函数和解决冲突的方法后,在求出散列表的基础上计算出查找成功时的平均查找长度和查找不成功的平均查找长度。
写在后面
参考资料
[1]王道408教材(2025版)
[2]王道课程资料





发表评论