hashval %= tablesize;
if (hashval < 0) hashval += tablesize;
return hashval;
}
这个散列函数涉及关键字中所有字符,并且一般可以分布的很好,它计算下面这个公式,并将结果限制在适当的范围内。
∑ i = 0 k e y s i z e − 1 k e y [ k e y s i z e − i − 1 ] ∗ 2 7 i \displaystyle\sum_{i=0}^{keysize-1} key[keysize - i- 1] * 27^i i=0∑keysize−1key[keysize−i−1]∗27i
程序这里根据 horner 法则计算一个(27的)多项式函数。例如:
计算 h k = h 0 + 27 k 1 + 2 7 2 k 2 h_k = h_0 + 27k_1 + 27^2k_2 hk=h0+27k1+272k2 是借助公式 h k = ( ( k 2 ) ∗ 27 + k 1 ) ∗ 27 + k 0 h_k = ((k_2) * 27 + k_1)* 27 + k_0 hk=((k2)∗27+k1)∗27+k0 进行。 horner 法则将其扩展到用于 n 次多项式。
这个散列函数利用到事实:允许溢出。这可能会引进负的数,因此在代码后面做了兼容。
上面这个散列函数未必是最好的,但却是具有极其简单的优点而且速度也很快。如果关键字特别长,那么散列函数计算将会花费过多的时间。有些程序设计人员通过只使用奇数位置上的字符来实现它们的散列函数。这里有这么一层想法:用计算散列函数节省下的时间来补偿由此产生的对均匀分布的函数的轻微干扰。
剩下的主要编程细节是解决冲突的消除问题。如果当一个元素被插入时与一个已经插入的元素散列到相同的值,那么就产生一个冲突,这个冲突需要消除。解决这种冲突的方法有几种,我们将讨论其中最简单的两种:分离链接法和开放定址法。
1、分离链接法
分离链接法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看下面我画的图,在散列表中,每个桶(bucket)或槽(slot)会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。我这里是 hash(x) = x mod 4举的例子。
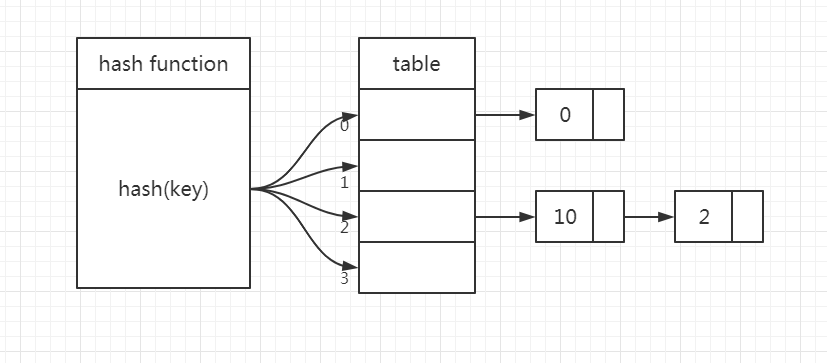
当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。实际上&#x

发表评论