目录
1 逻辑回归原理
2 sigmoid函数
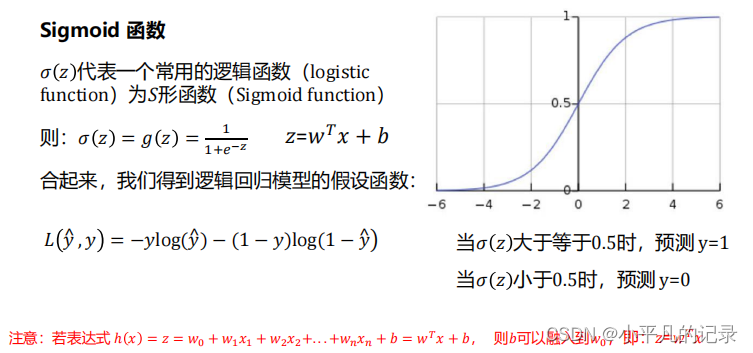
3 逻辑回归理论公式推导
——模型

——策略(定义损失函数)
求解w,定义一个指标衡量w的表现,即代价函数,利用最大似然法。

——算法(梯度下降法)
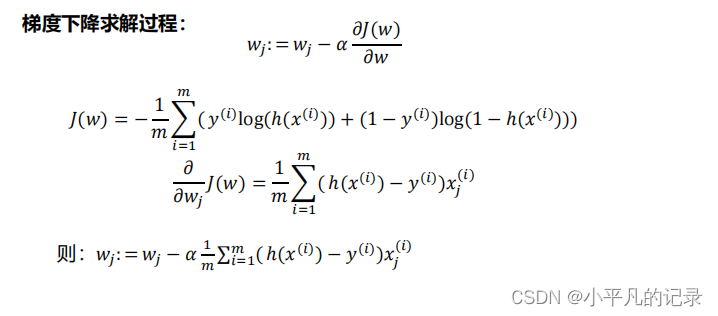


4 逻辑回归算法的改进——正则化
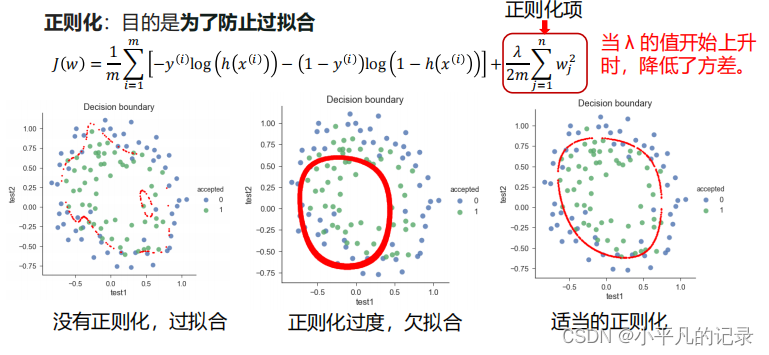
5 matlab实践
%% 原始数据
%一系列不同重量的车
weight = [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';
%各个重量类型的车的数目
tested = [48 42 31 34 31 21 23 23 21 16 17 21]';
%每个重量的车辆在测试中fail掉的数目
failed = [1 2 0 3 8 8 14 17 19 15 17 21]';
%故障率
proportion = failed ./ tested;
figure(1)
plot(weight,proportion,'s')
xlabel('重量');ylabel('比例');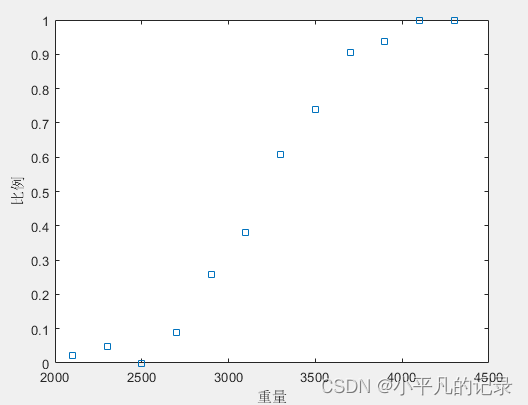
%% 线性拟合
%ployfit(x,y,n)执行多项式拟合,n代表多项式阶数,当n=1时,表示线性关系,返回多项式系数
linearcoef = polyfit(weight,proportion,1)
%value = ployval(p,x)返回多项式的值,p是多项式系数,降序排列
linearfit = polyval(linearcoef,weight);
figure(2)
line2 = plot(weight,proportion,'s',weight,linearfit,'r-',[2000 4500],[0 0],'k:',[2000 4500],[1,1],'k:');
xlabel('重量');ylabel('比例');
set(gcf,'position',[100 100 350 280]);
set(gca,'fontsize',9);
set(line2,'linewidth',1.5)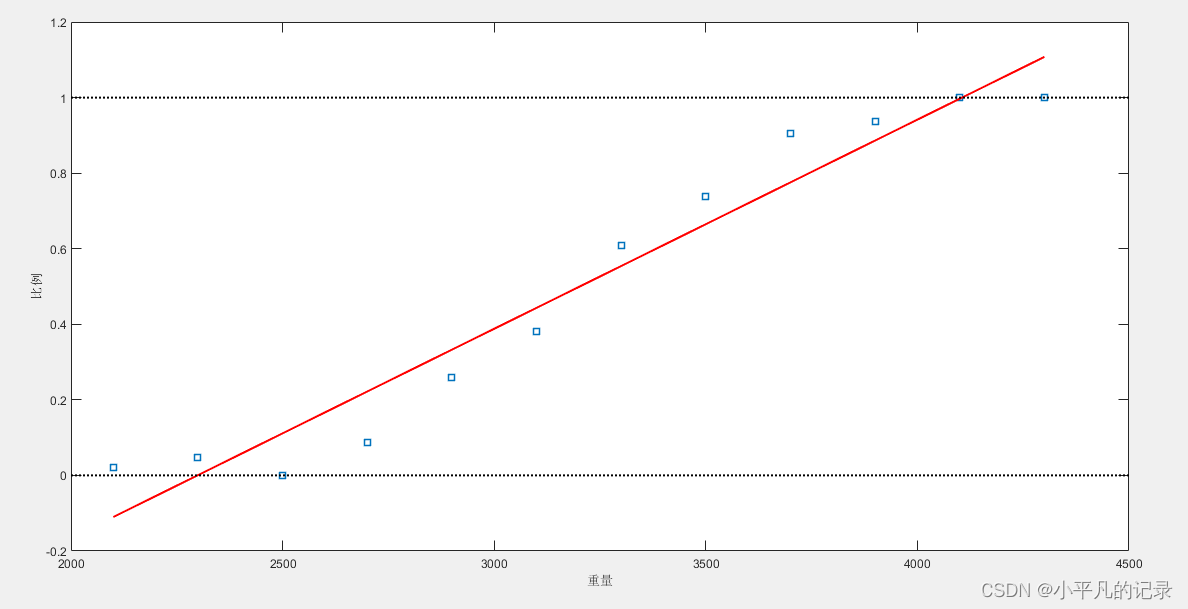
%% 多项式拟合
%区别在于这里选用3阶多项式,返回的stats是一个结构体,作为polyval函数的输入
%可用于误差估计,ctr包含了均值和方差,可用于对输入x归一化
[cubiccoef,stats,ctr] = polyfit(weight,proportion,3)
cubicfit = polyval(cubiccoef,weight,[ ],ctr); %利用归一化的weight进行多项式拟合
figure(3)
line = plot(weight,proportion,'s',weight,cubicfit,'r-',[2000 4500],[0 0],'k:',[2000 4500],[1,1],'k:');
xlabel('重量');ylabel('比例');
set(gcf,'position',[100 100 350 280]);
set(gca,'fontsize',9);
set(line,'linewidth',1.5)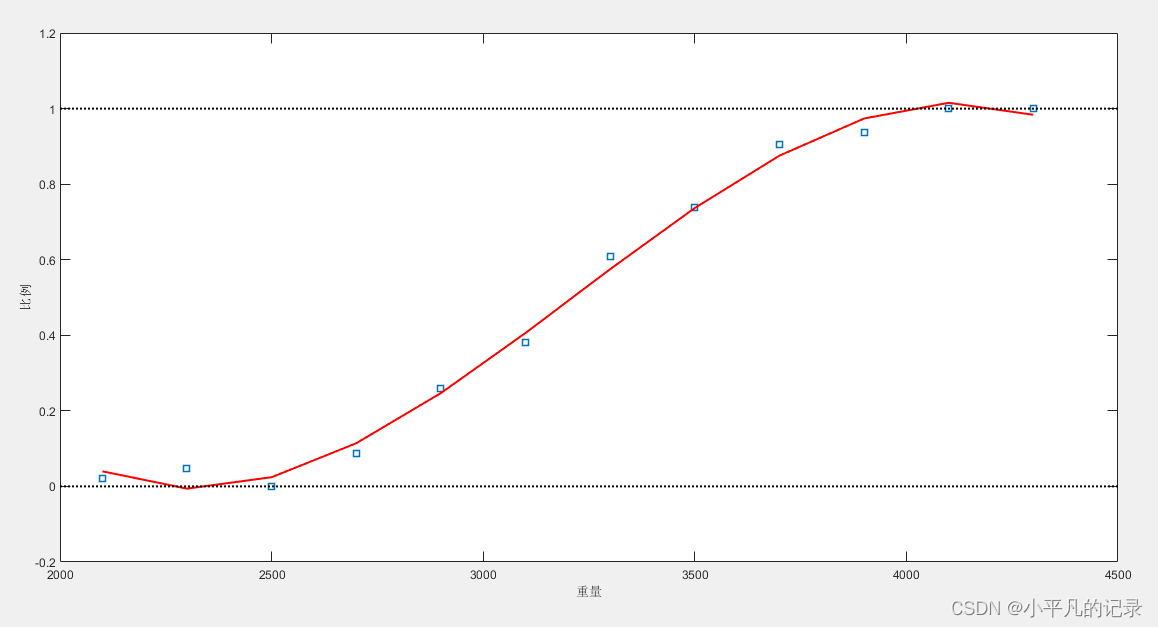
%% glmfit拟合
% 在glmfit中一般response是一个列向量,但是当分布是二项分布时,y可以是一个二值向量,
% 表示单次观测中成功还是失败,也可以是一个两列的矩阵,第一列表示成功的次数(目标出现的次数),
% 第二列表示总共的观测次数,因此这里y=[failed,tested]
% 另外指定distri='binomal',link='logit'
[logitcoef1,dev1] = glmfit(weight,[failed tested],'binomial','logit');
% glmval用于测试拟合的模型,计算出估计的y值
logitfit = glmval(logitcoef1,weight,'logit');
figure(4)
line3 = plot(weight,proportion,'bs',weight,logitfit,'r-');
xlabel('重量');ylabel('比例');
set(gcf,'position',[100 100 350 280]);
set(gca,'fontsize',9);
set(line3,'linewidth',1.5)
legend('数据','logistics回归')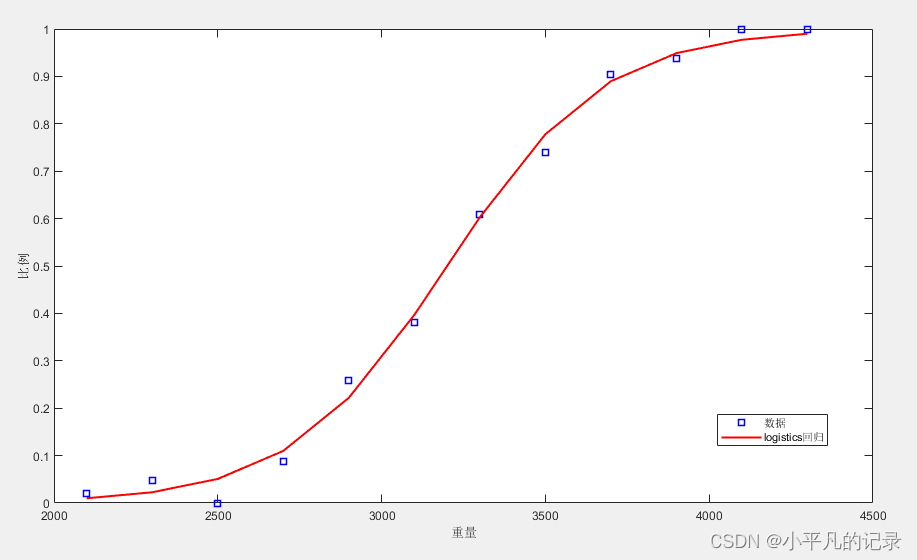
%% 预测
[logitcoef,dev,stats] = glmfit(weight,[failed tested],'binomial','logit');
normplot(stats.residp);
weightpred = 2500:500:4000;
% dlo和dhi是置信区间的下限和上限
[failedpred,dlo,dhi] = glmval(logitcoef,weightpred,'logit',stats,0.95,100);
figure(5)
line = errorbar(weightpred,failedpred,dlo,dhi,'r:');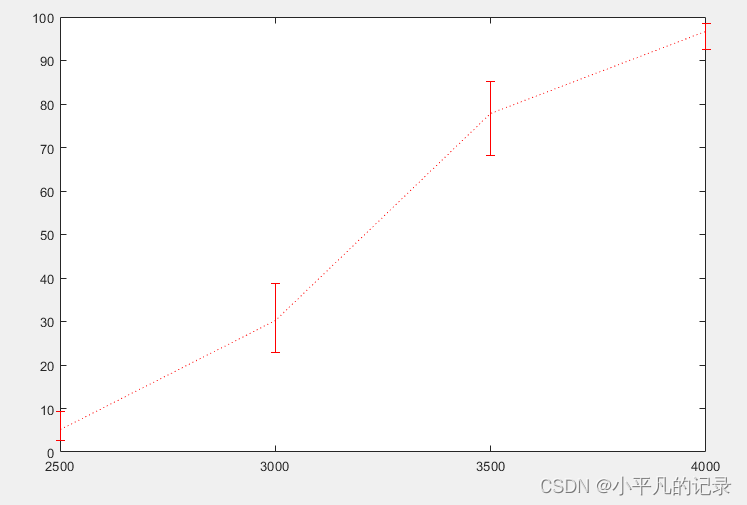
python参考:



发表评论