1、什么是逻辑回归?
虽然名字叫“逻辑回归”,但是逻辑回归是一个分类算法。只要用于进行二分类,即分类结果只有两种。例如:是否患病?是否为垃圾邮件?广告是否点击?
逻辑回归执行过程如下:
1、输入:线性回归的输出作为逻辑回归的输入,即输入为权重表达式
2、激活函数:回归的结果输入到
s
i
g
m
o
i
d
sigmoid
sigmoid函数中,
s
i
g
m
o
i
d
sigmoid
sigmoid函数表达式为:
1
1
+
e
−
x
\frac1{1+e^{-x}}
1+e−x1,其输出结果是在
(
0
,
1
)
(0,1)
(0,1)之间,默认
0.5
0.5
0.5为阈值
3、假设函数/线性模型:即将线性回归的输出结果(权重表达式)代入到激活函数里面,得到
y
=
1
1
+
e
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
.
.
.
+
w
j
x
j
+
b
y=\frac1{1+e^{w_1x_1+w_2x_2+w_3x_3+...+w_jx_j}}+b
y=1+ew1x1+w2x2+w3x3+...+wjxj1+b 其中
b
b
b为偏置
4、损失函数:对数似然损失,公式为
l
(
w
,
b
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
y
^
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
y
^
(
i
)
)
]
\mathcal{l}(\mathbf{w},b)=-\frac{1}{m}\sum_{i=1}^{m}\left[y^{(i)}\log(\hat{y}^{(i)})+(1-y^{(i)})\log(1-\hat{y}^{(i)})\right]
l(w,b)=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
其中,
m
是样本数量,
y
^
(
i
)
是第
i
个样本的预测概率,
y
(
i
)
是第
i
个样本的真实
标签。
\begin{aligned}&\text{其中,}m\text{ 是样本数量,}\hat{y}^{(i)}\text{ 是第 }i\text{ 个样本的预测概率,}y^{(i)}\text{ 是第 }i\text{ 个样本的真实}\\&\text{标签。}\end{aligned}
其中,m 是样本数量,y^(i) 是第 i 个样本的预测概率,y(i) 是第 i 个样本的真实标签。
5、优化损失:梯度下降
# 逻辑回归api调用
api:sklearn.linear_model.logisticregression(solver='liblinear',penalty='l2',c=1.0)
solver:优化求解方式(默认为开源的liblinear库实现
"""
penalty: 正则化类型。默认值:'l2'
solver: 优化算法。默认值:'lbfgs'
可选值:'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'
描述:用于优化问题的算法。不同的solver支持不同的正则化。
max_iter: 最大迭代次数。
默认值:100
描述:求解器收敛的最大迭代次数。
c: 正则化强度的倒数。
默认值:1.0
描述:必须为正数。较小的值指定更强的正则化。
"""
2、混淆矩阵
在分类任务下,预测结果与正确标记之间存在的四种不同组合,构成混淆矩阵
tp(真正例) ----真实结果为真,预测结果也为真
tn(真反例) ----真实结果为假,预测结果也为假
fp(伪正例) ----真实结果为假,预测结果为真
fn(伪反例) ----真实结果为真,预测结果为假

3、精确率和召回率
精确率:预测结果为正例的结果中真实为正例的比例
精确率
=
t
p
t
p
+
f
p
=\frac{tp}{tp+fp}
=tp+fptp
召回率:真实为正例的结果中预测结果为正例的比例,反映对正样本的区分能力
召回率
=
t
p
t
p
+
f
n
=\frac{tp}{tp+fn}
=tp+fntp
f1-score: 衡量模型的稳健性
f
1
−
s
c
o
r
e
=
2
t
p
2
t
p
+
f
n
+
f
p
f1-score=\frac{2tp}{2tp+fn+fp}
f1−score=2tp+fn+fp2tp
sklearn.metrics.classification_report(y_true,y_predict,labels=[],target_names=none)
"""
y_true:真实值
y_predict:预估器的预测值
labels:指定类别对应的数字
target_names:目标类别名称
return:每个类别的精确率和召回率
"""
4、roc曲线和auc指标1、tpr和fpr
tpr:
t
p
r
=
t
p
t
p
+
f
n
tpr=\frac{tp}{tp+fn}
tpr=tp+fntp 所有真实类别为1的样本中,预测类别为1的比例 ----召回率
fpr:
f
p
r
=
f
p
f
p
+
t
n
fpr=\frac{fp}{fp+tn}
fpr=fp+tnfp 所有真实类别为0的样本中,预测类别为1的比例
当tpr等于fpr时,预测效果为random guess(瞎猜)
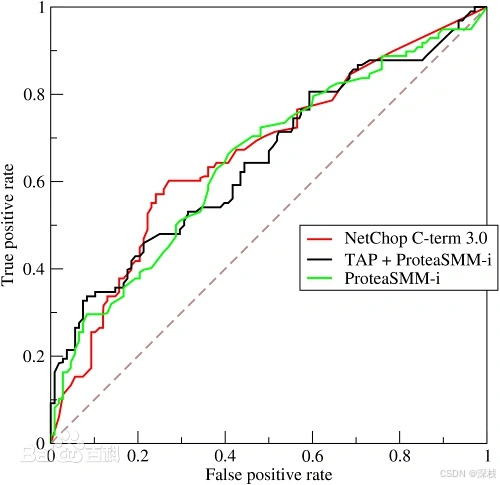
roc曲线(receiver operating characteristic curve)是通过改变分类阈值绘制出的tpr(true positive rate)和fpr(false positive rate)之间的关系图。
auc(area under the roc curve)是roc曲线下的面积,反映模型区分正负样本的能力。auc值在0.5到1之间,越接近1,模型效果越好。
4、逻辑回归案例——癌症预测(数据集)
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import standardscaler
from sklearn.linear_model import logisticregression
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
data = pd.read_csv(r"e:\python_learning\py基础\machine_learning\breastcancer.csv")
# 缺失值处理,缺失值为?先替换为np.nan,再删除缺失值
# 1)替换成np.nan
data = data.replace(to_replace="?", value=np.nan)
# 2)删除确实值,以样本为单位
data.dropna(inplace=true)
# 特征集和目标集切分
x = data.iloc[:, 2:-1]
y = data['class']
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y)
# 归一化
transfer = standardscaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 预估器预测
estimator = logisticregression()
estimator.fit(x_train, y_train)
print(f"逻辑回归的偏置为{estimator.intercept_}")
print(f"逻辑回归的参数为{estimator.coef_}")
y_predict = estimator.predict(x_test)
print("预测结果如下", y_predict)
print("预测值与真实值比对:", y_predict == y_test)
print("该模型准确率为", estimator.score(x_test, y_test))
report = classification_report(y_test, y_predict, labels=[2, 4], target_names=['良性', '恶性'])
print(report)
# auc和roc计算,每个真是样本必须为0(正例)、1(反例)
# 将y_test 转换0,1
np.where(y_test > 3, 1, 0)
print(f"该模型auc指标为{roc_auc_score(y_test, y_predict)}")
运行结果如下:
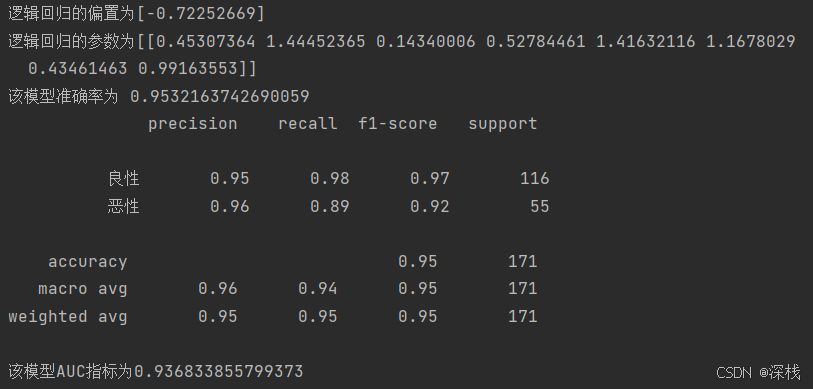
对于癌症检查,虽然正确率已经达到了
95.3
%
95.3\%
95.3%,但是对于这类较为严肃的问题,我们认为还是比较低,读者可以使用网格搜索和交叉验证(gridsearchcv)来找到最佳的超参数和最佳正确率。

发表评论