代码随想录算法训练营day3 | 203.移除链表元素、707.设计链表、206.反转链表

链表的定义

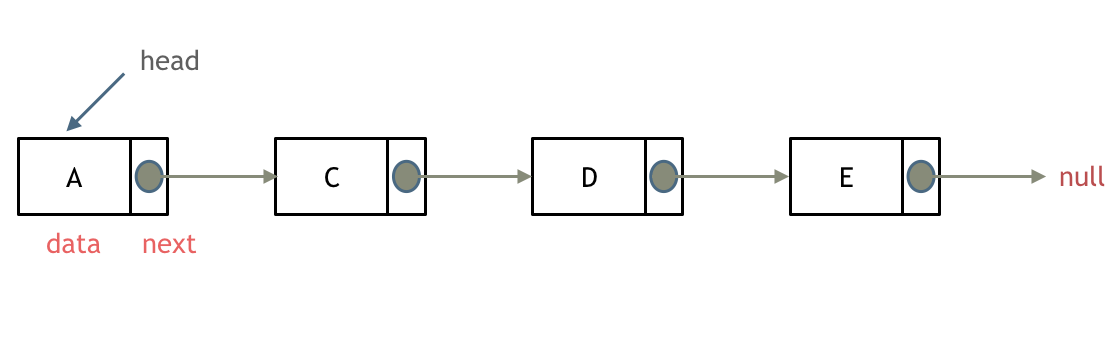
链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针）

c++中链表的定义：

struct listnode
{
    int val;
    listnode *next;
    listnode(int x) : val(x), next(null); // 构造函数，接受参数x，将x赋值给val，next赋值为null
};

如果不自行定义构造函数，c++也会默认生成一个构造函数，但是默认的构造函数不会初始化任何成员变量，举例：

• 自己定义构造函数初始化节点：

  listnode* head = new listnode(5);
  
  

• 使用默认构造函数初始化节点：

  listnode* head = new listnode();
  head->val = 5;	// 不能直接给变量赋值
  
  

链表的类型

单链表

指针域只能指向节点的下一个节点

双链表

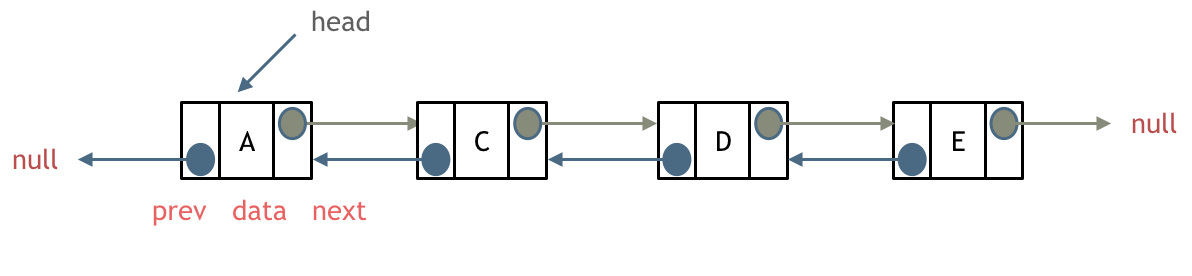
每一个节点有两个指针域prev和next，prev指向前一个节点，next指向后一个节点，因此双链表既可以向前查询，也可以向后查询

循环链表

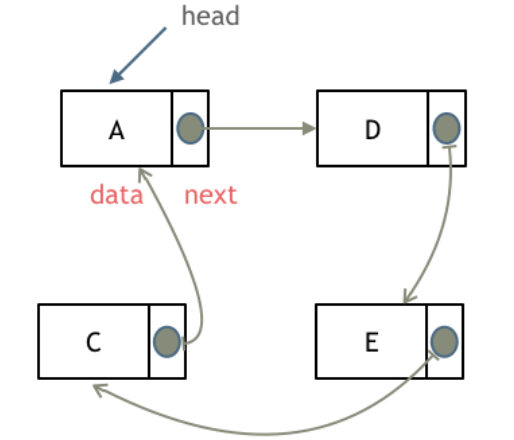
循环链表首尾相连，可以用来解决约瑟夫环问题

链表的操作

删除节点

删除节点d

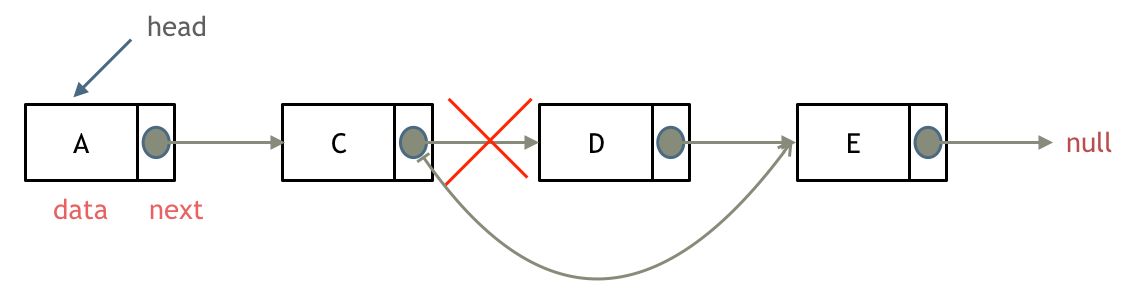
操作：节点c的next指向节点e，然后再手动释放这个d节点，释放这块内存：

c->next = d->next;
delete(d);

添加节点

添加节点f

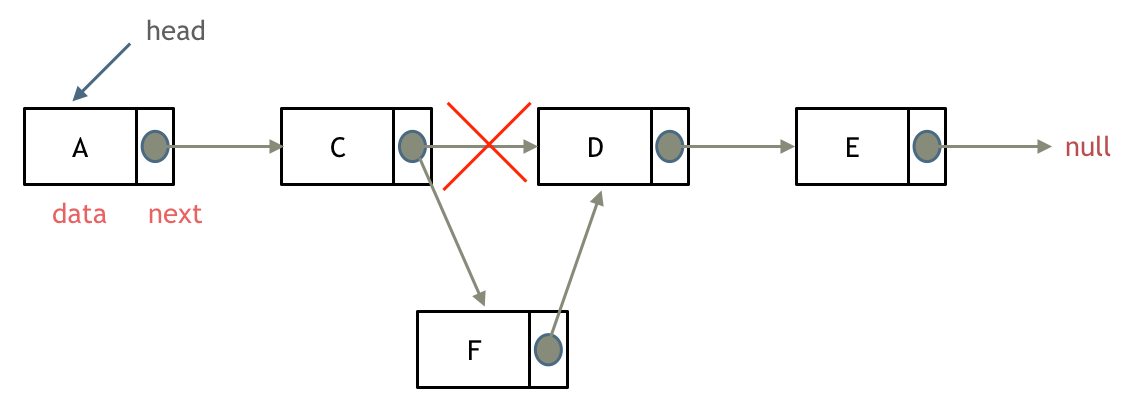
操作：首先节点f的next指针指向节点d，然后节点c的next指针指向f。顺序不能变，否则会丢失节点d的地址

f->next = c->next;	// 节点f指向节点d
c->next = f;		// 节点c指向节点f

与数组比较，链表的操作都是o(1)操作，不会影响其他节点，所以链表的增删操作比数组的增删操作更加简单。但是，如果要定位链表中的某一个节点，需要从头节点开始查找，遍历大量的节点。查找的时间复杂度为o(n)

c++链表容器

一般使用std::list创建双向链表结构：

std::list<int> list1 = {1, 2, 3, 4, 5};	//创建并初始化链表list1
std::list<int> list2 = (5, 100);	// 5个元素，每个初始化为100

插入和删除

#include <iostream>
#include <list>

int main() {
    std::list<int> mylist = {1, 2, 3, 4, 5};

    // 在开头插入
    mylist.push_front(0);  // mylist: 0, 1, 2, 3, 4, 5

    // 在末尾插入
    mylist.push_back(6);  // mylist: 0, 1, 2, 3, 4, 5, 6

    // 在指定位置插入
    auto it = mylist.begin();
    std::advance(it, 3);  // 前进 3 个位置
    mylist.insert(it, 10);  // mylist: 0, 1, 2, 10, 3, 4, 5, 6

    // 删除开头元素
    mylist.pop_front();  // mylist: 1, 2, 10, 3, 4, 5, 6

    // 删除末尾元素
    mylist.pop_back();  // mylist: 1, 2, 10, 3, 4, 5

    // 删除指定位置元素
    it = mylist.begin();
    std::advance(it, 2);  // 前进 2 个位置
    mylist.erase(it);  // mylist: 1, 2, 3, 4, 5

    return 0;
}

遍历

#include <iostream>
#include <list>

int main() {
    std::list<int> mylist = {1, 2, 3, 4, 5};

    // 使用迭代器遍历
    for (auto it = mylist.begin(); it != mylist.end(); ++it) {
        std::cout << *it << " ";
    }
    std::cout << std::endl;

    // 使用范围 for 循环遍历
    for (int value : mylist) {
        std::cout << value << " ";
    }
    std::cout << std::endl;

    return 0;
}

其它操作

#include <iostream>
#include <list>

int main() {
    std::list<int> mylist = {5, 3, 9, 1, 6};

    // 排序
    mylist.sort();  // mylist: 1, 3, 5, 6, 9

    // 合并另一个 list
    std::list<int> otherlist = {7, 8, 2};
    mylist.merge(otherlist);  // mylist: 1, 2, 3, 5, 6, 7, 8, 9

    // 反转
    mylist.reverse();  // mylist: 9, 8, 7, 6, 5, 3, 2, 1

    return 0;
}

203.移除链表元素

题目链接

解法一

直接使用原来的链表进行移除节点操作

被删除节点的前一个节点 指向 被删除节点的后一个节点prev->next = post。这种解法需要保留前置节点的信息（prev->next），而头节点没有前置节点，所以需要对头节点进行单独处理

头节点的处理：

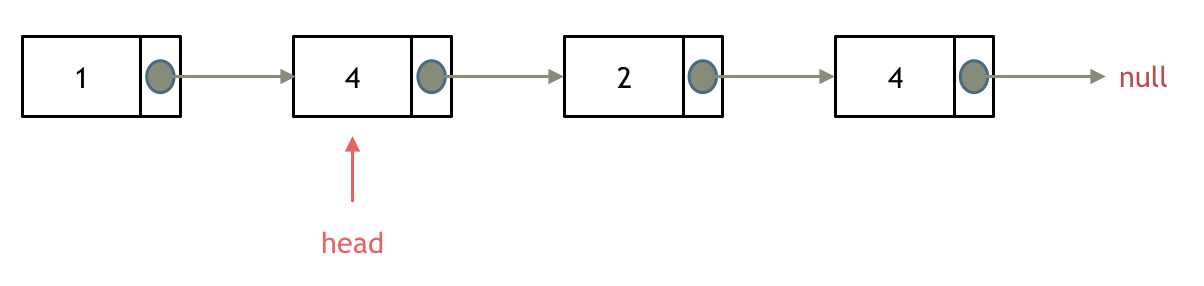
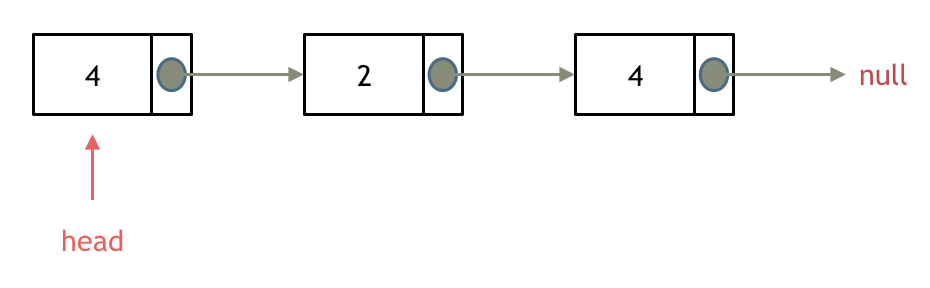
如果头节点的值 == 要删除的val，如图所示

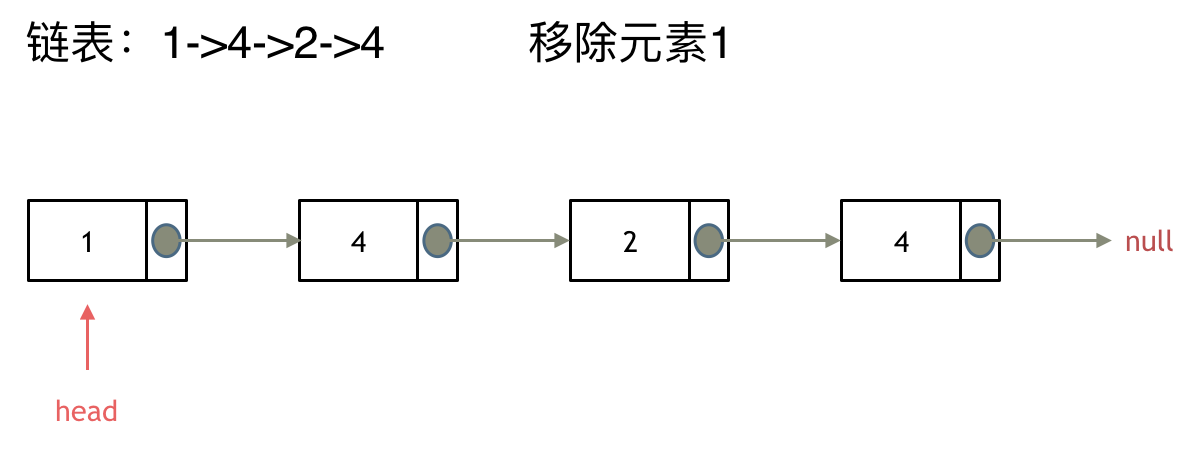
则需要将head指针后移，直至head->val != val，当前head指向的节点即为新的头节点

/**
 * definition for singly-linked list.
 * struct listnode {
 *     int val;
 *     listnode *next;
 *     listnode() : val(0), next(nullptr) {}
 *     listnode(int x) : val(x), next(nullptr) {}
 *     listnode(int x, listnode *next) : val(x), next(next) {}
 * };
 */
class solution {
public:
    listnode* removeelements(listnode* head, int val) {
        // 单独处理头节点，使head->val != val
        while(head != nullptr && head->val == val)
        {
            listnode* tmp = head;
            head = head->next;
            delete tmp; // c++需要手动释放节点
        }
        //  处理非头节点
        listnode* cur = head;   // 删除一个节点需要它前一个节点的信息，所以cur指向要删除节点的前一个节点
        while(cur != null && cur->next != null)
        {
            if(cur->next->val == val)
            {
                listnode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            }else
            {
                cur = cur->next;
            }
        }
        return head;
    };

};

解法二

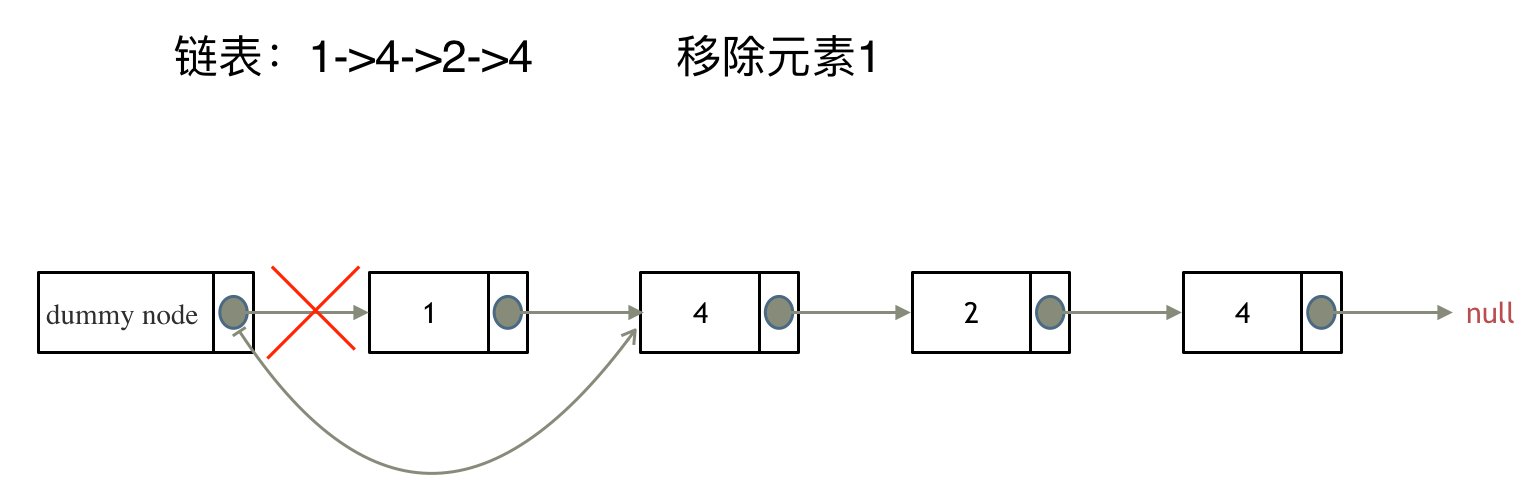
设置一个虚拟头节点再进行移除节点操作

我们想用统一的方式删除节点，不想单独处理头节点，那么就需要在头节点前增加一个虚拟头节点。移除任何一个节点（头节点 和 非头节点），只需要让 被删除节点的前一个节点 指向 被删除节点的后一个节点，即prev->next = post。对于头节点，它的前一个节点prev为虚拟头节点

/**
 * definition for singly-linked list.
 * struct listnode {
 *     int val;
 *     listnode *next;
 *     listnode() : val(0), next(nullptr) {}
 *     listnode(int x) : val(x), next(nullptr) {}
 *     listnode(int x, listnode *next) : val(x), next(next) {}
 * };
 */
class solution {
public:
    listnode* removeelements(listnode* head, int val) {
        // 设置虚拟节点
        listnode* dummyhead = new listnode(0);
        dummyhead->next = head;
        listnode* cur = dummyhead;
        // 从head节点开始删除
        while(cur->next != nullptr)
        {
            if(cur->next->val == val)
            {
                listnode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            }else
            {
                cur = cur->next;
            }
        }
        // 更新头节点，注意真正的头节点是dummyhead的下一个节点
        head = dummyhead->next;
        delete dummyhead;
        return head;
    };

};

总结

本题关键是要理解 虚拟头节点的使用技巧，这个对链表题目很重要

707.设计链表

题目链接

这道题目把链表常见的五个操作都覆盖到了

题目描述：

实现 mylinkedlist 类：

• mylinkedlist() 初始化 mylinkedlist 对象。
• int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
• void addathead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
• void addattail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
• void addatindex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。
• void deleteatindex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

思路

这道题目设计链表的五个接口：

• 获取链表第index个节点的数值
• 在链表的最前面插入一个节点
• 在链表的最后面插入一个节点
• 在链表第index个节点前面插入一个节点
• 删除链表的第index个节点

这五个接口已经覆盖了链表的常见操作，是练习链表的非常好的一道题目

设置一个虚拟头节点进行如上操作，这比 直接在原来的链表上操作 更加方便

// 链表的增删改查，使用虚拟头节点
class mylinkedlist {
public:
// 定义链表节点
struct listnode
{
    int val;
    listnode* next;
    listnode() : val(0), next(nullptr){};
    listnode(int val) : val(val), next(nullptr){};
};
// 链表的构造函数
    mylinkedlist() {
        _dummynode = new listnode();
        _size = 0;
    }
    
    int get(int index) {
        if(index >= _size || index < 0)
        {
            return -1;
        }
        listnode* cur = _dummynode->next;
        for(int i=0; i<index; ++i)
        {
            cur = cur->next;
        }
        return cur->val;
    }
    // 在链表的最前面插入一个节点，新插入的节点就是链表新的头节点
    void addathead(int val) {
        listnode* newnode = new listnode(val);
        newnode->next = _dummynode->next;
        _dummynode->next = newnode;
        _size++;
    }
    // 在链表的最后面插入一个节点
    void addattail(int val) {
        listnode* newnode = new listnode(val);
        listnode* cur = _dummynode;
        while(cur->next != nullptr)
        {
            cur = cur->next;
        }
        cur->next = newnode;
        _size++;
    }
    // 在序号为index的节点之前插入一个节点，这个节点将是新链表中序号为index的节点
    void addatindex(int index, int val) {
        if(index <= _size && index >= 0)	// 若index == size，则在链表的最后面插入一个节点
        {
            listnode* newnode = new listnode(val);
            listnode* cur = _dummynode;
            // 获得序号为index-1的节点cur
            for(int i=0; i<index; ++i)
            {
                cur = cur->next;
            }
            newnode->next = cur->next;
            cur->next = newnode;
            _size++;
        }
    }
    
    void deleteatindex(int index) {
        if(index < _size && index >= 0)    // index == size是不允许的
        {
            listnode *cur = _dummynode;
            for(int i=0; i<index; ++i)
            {
                cur = cur->next;
            }
            // 获得序号为index-1的节点
            listnode *tmp = cur->next;
            cur->next = cur->next->next;
            delete tmp;
            tmp = nullptr;
            _size--;
        }
    }
    private:
    listnode* _dummynode;
    int _size;
};

/**
 * your mylinkedlist object will be instantiated and called as such:
 * mylinkedlist* obj = new mylinkedlist();
 * int param_1 = obj->get(index);
 * obj->addathead(val);
 * obj->addattail(val);
 * obj->addatindex(index,val);
 * obj->deleteatindex(index);
 */

206.反转链表

题目链接

改变链表的next指针指向即可完成链表的反转

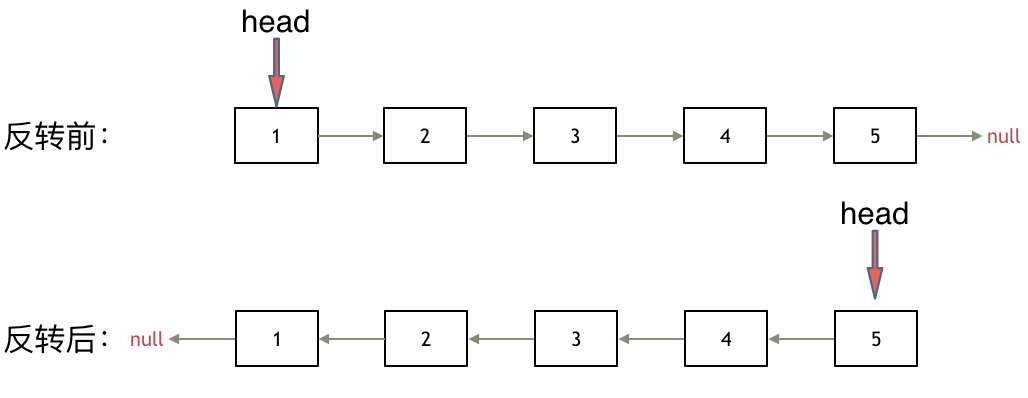
双指针法

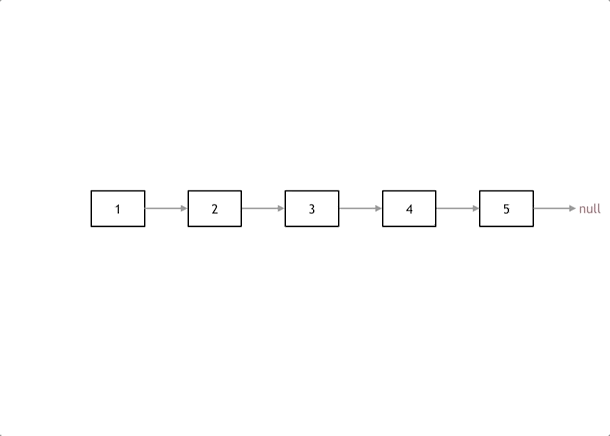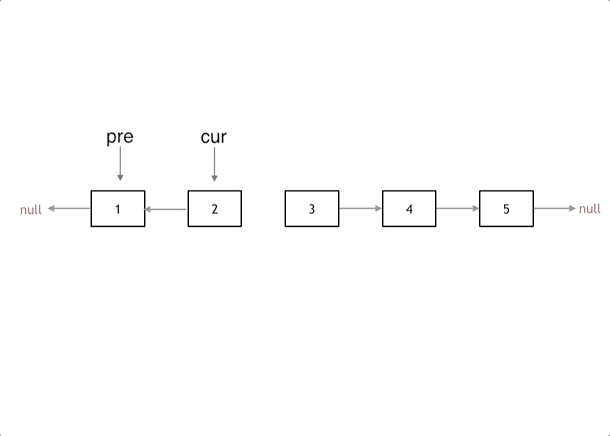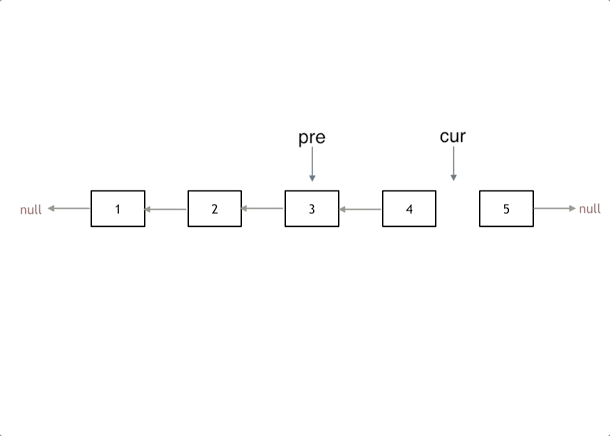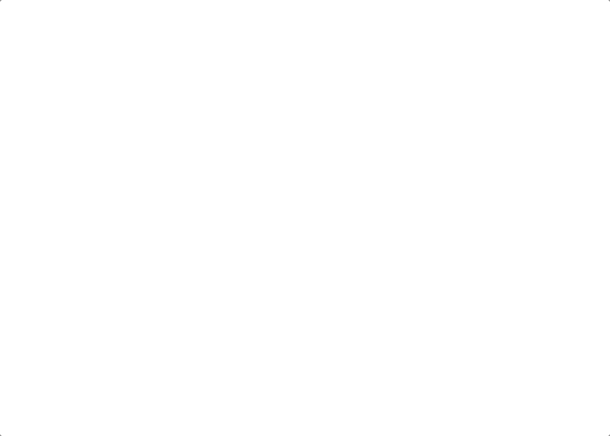
初始化：cur指向头节点，prev初始化为nullptr（prev定义为nullptr，使head节点指向nullptr）

循环过程：反转过程中，首先使用tmp保存cur->next节点，然后改变cur节点的指向，即cur->next = prev，反转cur节点，最后移动cur和prev：prev = cur; cur = tmp;

循环终止：当cur指向nullptr时，循环结束。此时完成了链表的反转，prev是新的头节点

/**
 * definition for singly-linked list.
 * struct listnode {
 *     int val;
 *     listnode *next;
 *     listnode() : val(0), next(nullptr) {}
 *     listnode(int x) : val(x), next(nullptr) {}
 *     listnode(int x, listnode *next) : val(x), next(next) {}
 * };
 */
class solution {
public:
    listnode* reverselist(listnode* head) {
        listnode* tmp;	// 保存cur的下一个节点
        listnode* cur = head;
        listnode* prev = nullptr;
        while(cur)
        {
            tmp = cur->next;	// 保存cur->next节点
            cur->next = prev;	// 反转cur节点
            // 更新prev 和 cur指针
            prev = cur;
            cur = tmp;
        }
        return prev;
    }
};

递归法

递归和循环是等价的，循环能做的事递归都能做，反之亦然

运用递归的关键在于：明确你的递归函数的功能，然后相信它能完成这个功能。这种“相信”称为leap of faith，首先相信一些结论，然后再用它们去证明另外一些结论。如果你相信你正在写的递归函数是正确的，并调用它，然后在此基础上写完这个递归函数，那么它就会是正确的，从而值得你相信它正确。

设计递归时，要将整个过程分为一步+无数步，“一步”在每次递归过程中完成，“无数步”就是递归函数要实现的功能，比如反转链表的递归过程=反转当前节点（一步，每次递归都要实现）+ 反转当前节点之后的所有节点（无数步，递归函数的功能）

递归的终止条件为 最后一次递归完成时的判断条件。我们可以将思绪直接跳到递归的最后一步，想一想递归中的最后一步做了什么，有什么特殊的判断条件

参照双指针法的思路，我们给出递归实现

// 递归法
/**
 * definition for singly-linked list.
 * struct listnode {
 *     int val;
 *     listnode *next;
 *     listnode() : val(0), next(nullptr) {}
 *     listnode(int x) : val(x), next(nullptr) {}
 *     listnode(int x, listnode *next) : val(x), next(next) {}
 * };
 */
class solution {
public:
    // 相信reverse函数能够完成 从cur到末尾 所有节点的反转
    // 整个过程拆分为：先反转当前节点，然后递归反转当前节点之后的所有节点
    listnode* reverse(listnode* prev, listnode* cur)
    {
        // 终止条件
        if(cur == nullptr)
        {
            return prev;
        }
        // 首先反转当前节点
        listnode *tmp = cur->next;  // tmp是cur的下一个节点
        cur->next = prev;
        // 接下来递归反转tmp之后的所有节点
        return reverse(cur, tmp);
    };
    listnode* reverselist(listnode* head) {
        return reverse(nullptr, head);  // 初始，prev为nullptr，cur为head，这与双指针法是一样的
    }
};

除此之外，还可以从后向前反转指针指向。反转链表中的所有节点 = 先反转当前节点之后的所有节点（无数步） + 然后反转当前节点（一步）

class solution {
public:
    listnode* reverselist(listnode* head) {
        if(head == nullptr)
        {
            return nullptr;
        }
        if(head->next == nullptr)
        {
            return head;
        }
        // 首先反转当前节点之后的所有节点
        listnode* last = reverselist(head->next);
        // 然后反转当前节点
        head->next->next = head; // 令head的下一个节点指向head
        head->next = nullptr;    // 此时的head节点是尾节点，next需要指向nullptr
        return last;             // 这里返回的是原链表的最后一个节点，它是新链表中的头节点。实际上递归过程中没有使用这个返回值，而是像传递火炬一样，将终止条件 head->next = nullptr 中的head 逐级返回
    }
};

总结

今天是链表专题的第一天，涉及到链表的增删改查操作，以及最后的反转操作，难度适中。在链表中，设置一个虚拟头节点（大学课程里面叫它首节点，与头节点相区分）是一个常用的技巧，尤其是增删改查操作中，这方便对一些特殊条件的判断 和 对头节点进行处理。反转的双指针法很重要，双指针法巧妙地将链表反转等同于链表next指针的指向反转，注意要事先用tmp指针保存cur的下一个节点，否则在反转后会丢失原链表中cur下一个节点的信息。最后还利用反转链表这道题目复习了递归。递归是一种很有难（玄学）但是很有趣的设计思想。运用递归的关键在于相信你的递归函数能完成它要实现的功能，而 递归函数要实现什么功能 是在递归设计中明确的，递归设计的关键在于将整个问题拆分为一步+无数步，“一步”在每次递归过程中完成，“无数步”就是递归函数要实现的功能。一步 和 无数步的执行顺序是随意的，比如最后一道题，可以先 反转当前节点之后的所有节点（无数步），再 反转当前节点（一步），也可以先 反转当前节点（一步），再 反转当前节点之后的所有节点（无数步）