Openlayers实现角度测量的方法_Javascript

概述

在前面介绍了如何在 openlayers 中进行长度和面积的测量，可以参考：《openlayers 实现长度测量》,《》。

那么如何在 openlayers 中进行角度的测量呢？很遗憾ol/sphere模块中没有提供对应角度测量的 api 或方法，但是我们可以自己实现。

实践

效果展示

角度量测绘制

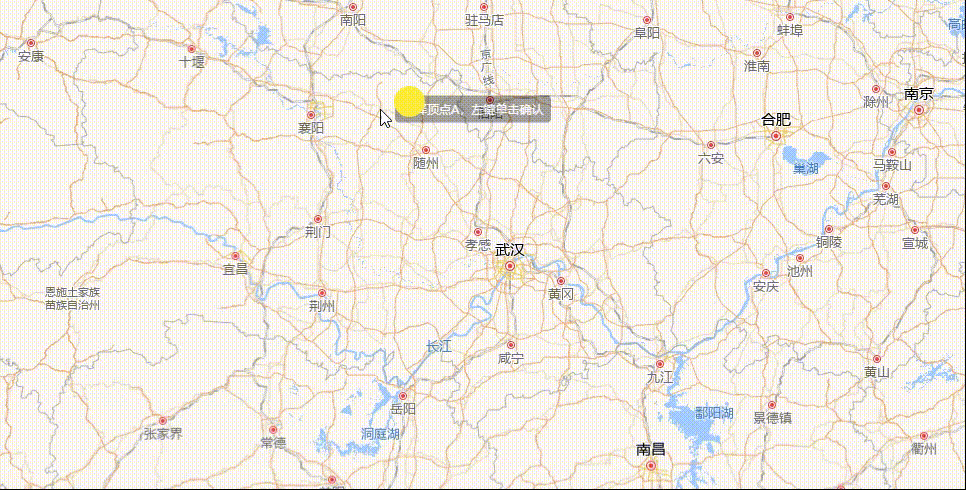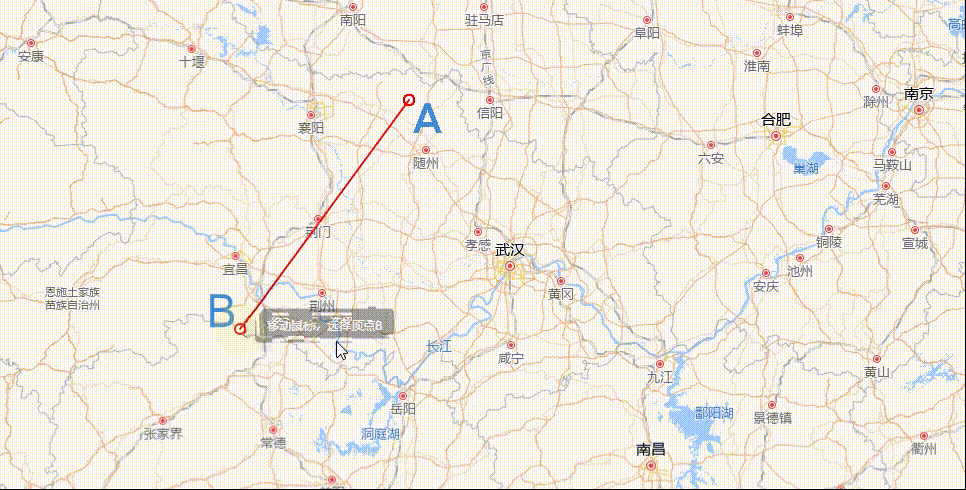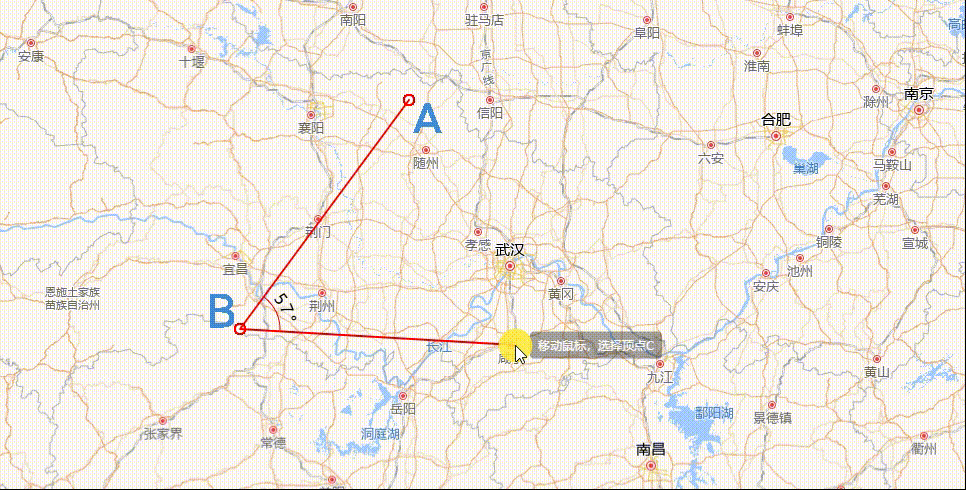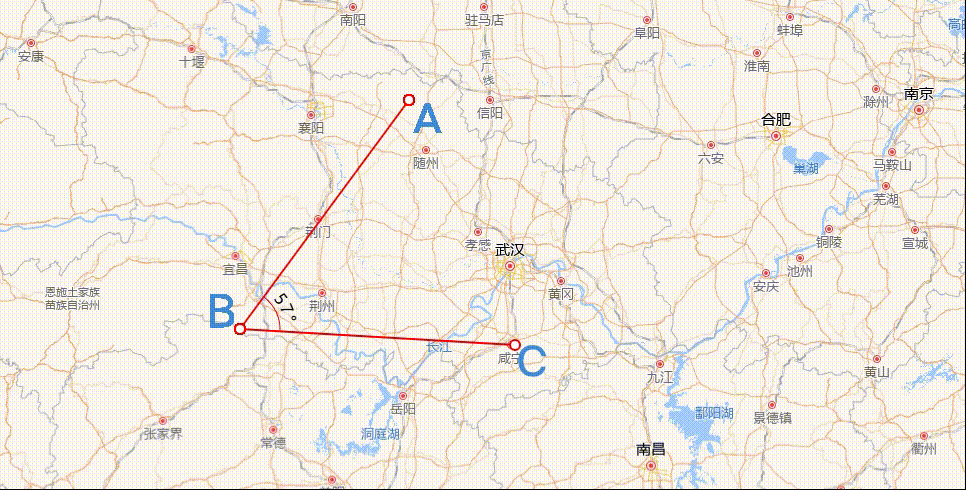
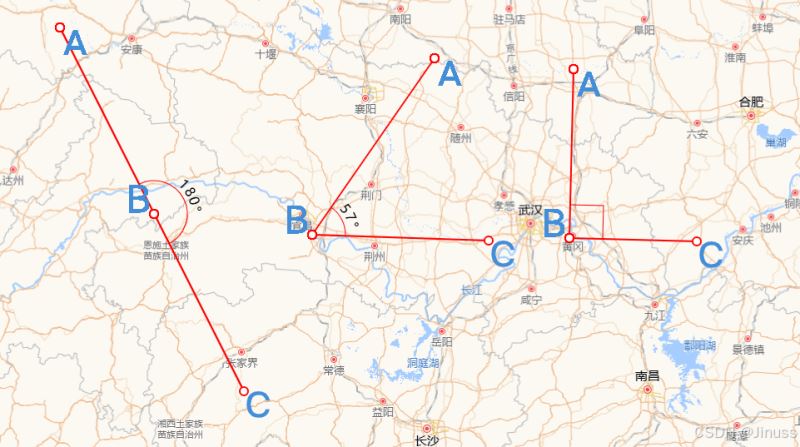
结果

实现思路

实现思路主要有两点：一是计算夹角的度数；二则是夹角的圆弧表示，上图中表示角度的圆弧，可以是 0 - 180° 中的任意一个角度，且它总是包裹在夹角内，连接夹角的两边。

夹角的度数计算

确定夹角

数学常识可知，夹角度数的区间必定是[0°，180°]，而且，夹角是由三个坐标点的位置确定大小的，如上图中的顶点a、b、c。因此，我们可以内定顶点 ∠abc是我们需要测量的夹角。

确定顶点坐标位置

可以在地图上随机取三个点作为顶点，但是这样并不科学，这样无法满足绘制特定角度的需求。选点还是通过ol/interaction模块的draw api 进行拾取。

但geom.getcoordinates()返回的坐标个数达到四个时，就调用this.draw.finishdrawing()方法结束绘制。因为它的返回值倒数的两个坐标都是一样的，因此即使我们只需要三个点的坐标，也需要等到它的返回值长度是4。

实现代码如下：

this.draw.on(
  "drawstart",
  (evt: { feature: feature<geometry>, coordinate: coordinate }) => {
    const { feature, coordinate } = evt;
    this.listengeometrychange = feature.getgeometry().on("change", (evt) => {
      const geom = evt.target;
      let startpoint = geom.getfirstcoordinate();
      this.addmarker({ coordinate: startpoint, symbolid: "a", anchor: [0, 0] });
      const coordinates = geom.getcoordinates().slice(0, -1);
      if (coordinates.length > 1) {
        this.addmarker({
          coordinate: coordinates[1],
          symbolid: "b",
          anchor: [1, 1],
        });
      }
      const pointscount = geom.getcoordinates();
      if (pointscount.length >= 4) {
        this.addmarker({
          coordinate: coordinates[2],
          symbolid: "c",
          anchor: [0, 0],
        });
        this.addanglemark({
          coordinate: coordinates[1],
          angles: calculateangle(coordinates),
        });
        this.draw.finishdrawing();
      }
    });
  }
);

如何计算夹角

两点的坐标位置决定了两点之间的距离，即当我们知道a、b和c的坐标后，就可以知道线段ab和bc的长度了，然后通过数据计算就可以知道 ∠abc的大小了。前面提到夹角的区间范围，因为在电脑中，夹角也可以是负值，这个取决于它对应的方向是顺时针还是逆时针方向，因此要保证夹角的范围在区间[0°，180°]内。

封装的计算夹角的方法calculateangle如下：

const calculateangle = (points: coordinate[]) => {
  // 提取坐标点 a, b, c
  const [a, b, c] = points;
  // 计算向量 ab 和 bc
  const ab = { x: b[0] - a[0], y: b[1] - a[1] };
  const bc = { x: c[0] - b[0], y: c[1] - b[1] };
  // 计算点积
  const dotproduct = ab.x * bc.x + ab.y * bc.y;
  // 计算向量的模
  const magnitudeab = math.sqrt(ab.x ** 2 + ab.y ** 2);
  const magnitudebc = math.sqrt(bc.x ** 2 + bc.y ** 2);
  // 计算余弦值
  const costheta = dotproduct / (magnitudeab * magnitudebc);
  // 确保 costheta 在 -1 和 1 之间
  const clippedcostheta = math.max(-1, math.min(1, costheta));
  // 计算夹角（弧度转换为度）
  const angleinradians = math.acos(clippedcostheta);
  const angleindegrees = angleinradians * (180 / math.pi);
  // 计算方向（使用叉积）
  const crossproduct = ab.x * bc.y - ab.y * bc.x;
  // 如果叉积为负
  const angle = crossproduct < 0 ? angleindegrees - 180 : 180 - angleindegrees;
  return angle;
};

夹角的圆弧

通过上面可以计算得到 ∠abc夹角的度数了，因为是自由绘制选点，因此无法保证ba或者bc是否与水平方向平行一致。小学时代，用量角器测量时，第一步就是需要保证量角器的底边与夹角的一边对齐，这样的测量结果才准确。但是在 openlayers 中，我们就是需要去实现这样一个量角器，无论在地图上选择哪三个顶点，圆弧都能准确表示角度。并且这个圆弧的长度不固定。

这个需求可以使用canvas或者svg实现，例子中是使用svg实现的。

svg 画一个圆弧

效果如下：

拖动滑块，可以动态绘制任意一段圆弧，其代码如下：

<svg width="200" height="200">
  <path id="arc" fill="none" stroke="blue" stroke-width="2" />
  <line
    id="radial1"
    x1="100"
    y1="100"
    stroke="red"
    stroke-width="2"
    stroke-dasharray="5,5"
  />
  <line
    id="radial2"
    x1="100"
    y1="100"
    stroke="red"
    stroke-width="2"
    stroke-dasharray="5,5"
  />
  <text fill="black" font-size="16" text-anchor="middle">
    <textpath href="#arc" rel="external nofollow"  startoffset="50%" side="left">
      <tspan dy="-5" id="text"></tspan>
    </textpath>
  </text>
</svg>

function drawarc(adjustedangle) {
  const endy = centery + radius * math.cos((adjustedangle * math.pi) / 180);
  const endx = centerx - radius * math.sin((adjustedangle * math.pi) / 180);
  const starty = centerx;
  const startx = centery - radius;
  const largearcflag = adjustedangle > 180 ? 0 : 1;
  const d_1 = `m ${startx} ${starty} a ${radius} ${radius} 0 ${largearcflag} 1 ${endx} ${endy}`; //表示非直角
  const d_2 = `m ${endx} ${endy} l ${startx} ${endy}  l${startx} ${starty}`; //表示直角
  const angle = math.abs(adjustedangle);
  let lastd = d_1;
  if (angle == 540) {
    lastd = d_2;
  }
  arcpath.setattribute("d", lastd);
  radial1.setattribute("x2", startx);
  radial1.setattribute("y2", starty);
  radial2.setattribute("x2", endx);
  radial2.setattribute("y2", endy);
}

圆弧贴图

现在需要将圆弧以overlay的方式添加到 ∠abc处就完事了，结果如下：

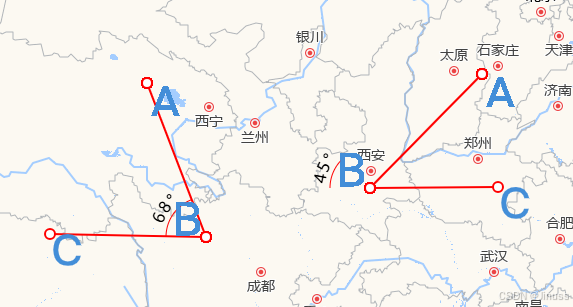
上面的情形就很诡异，因为圆弧始终是在水平位置，而我们选点是随意的，因此圆弧需要旋转一定的角度，使得圆弧的两边与夹角的两边对齐。但是具体旋转多少角度，逆时针旋转还是顺时针旋转？这个就取决于线段ba与bc的倾斜角度，准确来说是以顶点b为原点建立坐标系，水平方向为x轴且向右为x轴正半轴，垂直方向为y轴且向上为y轴正半轴。那么圆弧的旋转角度和方向就取决于ba和bc与x 轴负半轴的夹角。

和 css 中transform的rotate规则报纸一致，规定圆弧逆时针旋转为负，顺时针旋转为正。因此，我们可以规定如果ba（或者bc）在第三象限或者是第四象限，则它与x轴负半轴的夹角为负值；反之，如果在第一象限则为正数钝角，第二象限则为正数锐角

计算 ba 或者 bc 与 x 轴负半轴夹角

主要还是用到数学知识，代码如下：

function calculateanglepoint(points) {
  const [a, b, c] = points;
  const [ax, ay] = a;
  const [bx, by] = b;
  const [cx, cy] = c;
  // 计算向量 ba 和 bc
  const ba = { x: ax - bx, y: ay - by }; // ba 向量（从 b 到 a）
  const bc = { x: cx - bx, y: cy - by }; // bc 向量（从 b 到 c）
  // 计算 ba 和 bc 向量与 x 轴的夹角（单位：度）
  let angleba = math.atan2(ba.y, ba.x) * (180 / math.pi); // [-180, 180] 范围
  let anglebc = math.atan2(bc.y, bc.x) * (180 / math.pi); // [-180, 180] 范围
  // 计算 ba 向量与 x 轴负半轴的夹角
  if (angleba >= 0 && angleba < 90) {
    // 第一象限，夹角为正钝角
    angleba = 180 - angleba;
  } else if (angleba >= 90 && angleba <= 180) {
    // 第二象限，夹角为正锐角
    angleba = 180 - angleba;
  } else if (angleba < 0 && angleba >= -90) {
    // 第四象限，夹角为负钝角
    angleba = math.abs(angleba) - 180;
  } else {
    // 第三象限，夹角为负锐角
    angleba = math.abs(angleba) - 180;
  }
  // 计算 bc 向量与 x 轴负半轴的夹角
  if (anglebc >= 0 && anglebc < 90) {
    // 第一象限，夹角为正钝角
    anglebc = 180 - anglebc;
  } else if (anglebc >= 90 && anglebc <= 180) {
    // 第二象限，夹角为正锐角
    anglebc = 180 - anglebc;
  } else if (anglebc < 0 && anglebc >= -90) {
    // 第四象限，夹角为负钝角
    anglebc = math.abs(anglebc) - 180;
  } else {
    // 第三象限，夹角为负锐角
    anglebc = math.abs(anglebc) - 180;
  }
  return {
    angleba: angleba, // ba 向量与 x 轴负半轴的夹角
    anglebc: anglebc, // bc 向量与 x 轴负半轴的夹角
  };
}

确定旋转角度

由上得到了angleba和anglebc，毫无疑问，如果ba和bc在第一二象限，则圆弧需要顺时针旋转，且旋转角度为math.min(angleba,anglebc)，反之都在第三四象限，则旋转角度为- math.max(math.abs(angleba),math.abs(anglebc)),如果ba和bc在不同象限，那就要分情况讨论了，具体判断规则如下：

let rotate = 0;
if (angleba < 0 && anglebc < 0) {
  rotate = -math.max(math.abs(angleba), math.abs(anglebc));
}
if (angleba > 0 && anglebc > 0) {
  rotate = math.min(math.abs(angleba), math.abs(anglebc));
}
//第一二三象限 不同象限
if (angleba >= 135 && angleba <= 180 && anglebc <= -45 && anglebc >= -90) {
  rotate = angleba;
}
if (anglebc >= 135 && anglebc <= 180 && angleba <= -45 && angleba >= -90) {
  rotate = anglebc;
}
if (angleba >= 135 && angleba <= 180 && anglebc <= 0 && anglebc >= -45) {
  rotate = anglebc;
}
if (anglebc >= 135 && anglebc <= 180 && angleba <= 0 && angleba >= -45) {
  rotate = angleba;
}
if (angleba >= 90 && angleba <= 135 && anglebc <= 0 && anglebc >= -45) {
  rotate = anglebc;
}
if (anglebc >= 90 && anglebc <= 135 && angleba <= 0 && angleba >= -45) {
  rotate = angleba;
}
if (angleba >= 90 && angleba <= 135 && anglebc >= -90 && anglebc <= -45) {
  rotate = angleba;
}
if (anglebc >= 90 && anglebc <= 135 && angleba >= -90 && angleba <= -45) {
  rotate = anglebc;
}
if (angleba >= 0 && angleba <= 90 && anglebc <= 0 && anglebc >= -90) {
  rotate = anglebc;
}
if (anglebc >= 0 && anglebc <= 90 && angleba <= 0 && angleba >= -90) {
  rotate = angleba;
}
//第一二四象限不同象限
if (anglebc >= -180 && anglebc <= -90 && angleba <= 180 && angleba >= 90) {
  rotate = angleba;
}
if (angleba >= -180 && angleba <= -90 && anglebc <= 180 && anglebc >= 90) {
  rotate = anglebc;
}
if (anglebc >= -135 && anglebc <= -90 && angleba >= 0 && angleba <= 45) {
  rotate = anglebc;
}
if (anglebc >= -135 && anglebc <= -90 && angleba >= 45 && angleba <= 90) {
  rotate = angleba;
}
if (angleba >= -135 && angleba <= -90 && anglebc >= 0 && anglebc <= 45) {
  rotate = angleba;
}
if (angleba >= -135 && angleba <= -90 && anglebc >= 45 && anglebc <= 90) {
  rotate = anglebc;
}
if (anglebc >= -180 && anglebc <= -135 && angleba >= 0 && angleba <= 45) {
  rotate = anglebc;
}
if (anglebc >= -180 && anglebc <= -135 && angleba >= 45 && angleba <= 90) {
  rotate = angleba;
}
if (angleba >= -180 && angleba <= -135 && anglebc >= 0 && anglebc <= 45) {
  rotate = angleba;
}
if (angleba >= -180 && angleba <= -135 && anglebc >= 45 && anglebc <= 90) {
  rotate = anglebc;
}