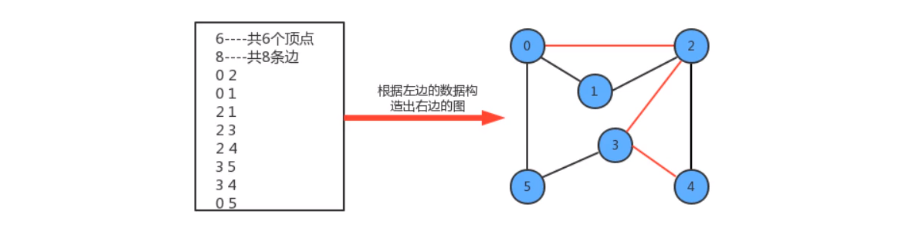
加权无向图中的边不能简单的使用v-w两个顶点表示了,而必须要给边 关联一个权重值,因此可以使用 对象 来描述一条边

- api
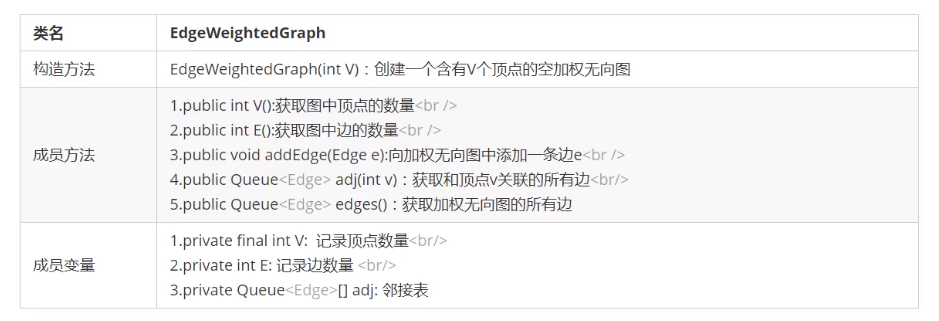
- 代码
package chapter17;
import chapter03.queue;
/**
-
@author 土味儿
-
date 2021/9/16
-
@version 1.0
-
加权无向图
*/
public class edgeweightedgraph {
/**
- 顶点
数量
*/
private final int vnum;
/**
- 边数量
*/
private int enum;
/**
- 邻接表
*/
private queue[] adj;
/**
-
构造器
-
@param vnum
*/
public edgeweightedgraph(int vnum) {
// 初始化顶点数量
this.vnum = vnum;
// 初始化边数量
this.enum = 0;
// 初始化邻接表
this.adj = new queue[vnum];
// 初始化邻接表中的空队列
for (int i = 0; i < vnum; i++) {
this.adj[i] = new queue();
}
}
/**
-
得到顶点数量
-
@return
*/
public int getvnum(){
return vnum;
}
/**
-
得到边数量
-
@return
*/
public int getenum(){
return enum;
}
/**
-
添加一条边v-w
-
@param e
*/
public void addedge(edge e){
// 因为是无向图,让边e同时出现在e的两个顶点的邻接表中
int v = e.either();
int w = e.other(v);
this.adj[v].enqueue(e);
this.adj[w].enqueue(e);
// 边数量加1
enum++;
}
/**
-
获取顶点v的所有相邻顶点
-
@param v
-
@return
*/
public queue adj(int v){
return this.adj[v];
}
/**
-
获取加权无向图中的所有边
-
@return
*/
public queue edges(){
// 创建一个队列对象,存储所有的边
queue alledges = new queue<>();
// 遍历图中的每一个顶点,找到每个顶点的邻接表,邻接表中存储了该顶点关联的每一条边
for(int v=0;v<vnum;v++){
// 遍历顶点v的邻接表,找到每一条和v关联的边
for (edge e : adj(v)) {
// 每条边的两个顶点,一大一小,判断大小再添加,可以避免重复
if(e.other(v) < v){
alledges.enqueue(e);
}
}
}
return alledges;
}
}
==================================================================
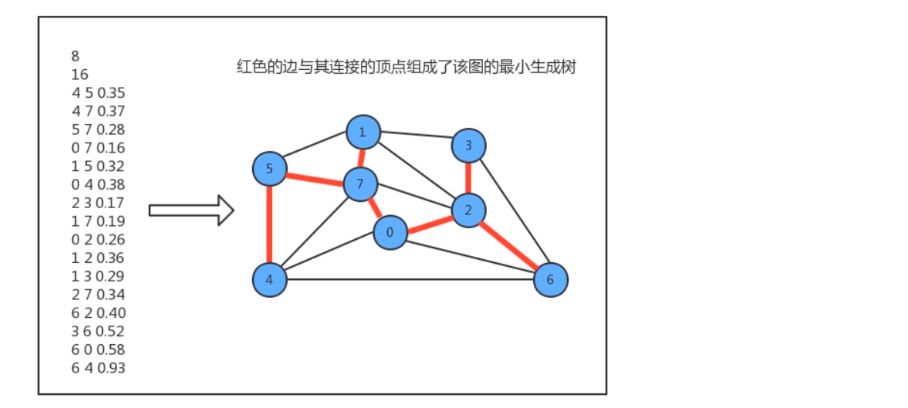
- 图的生成树 是它的一棵含有其 所有顶点 的 无环连通子图,一副加权无向图的最小生成树,是它的一棵权值(树中所有边的权重之和)最小的生成树
- 只考虑连通图
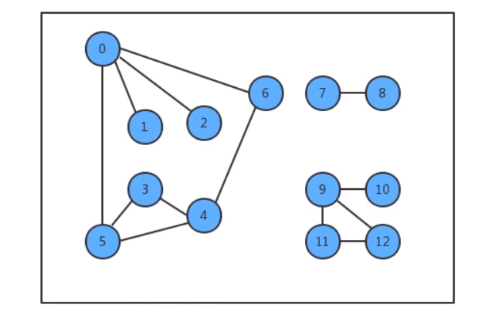
- 所有边的权重都各不相同
1)树的性质
- 用一条边连接树中的任意两个顶点都会产生 一个新的环
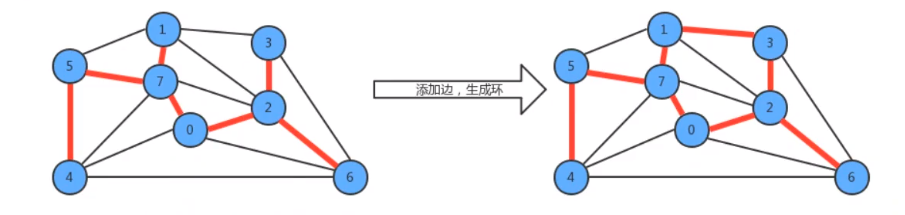
- 从树中删除任意一条边,将会得到 两棵独立的树
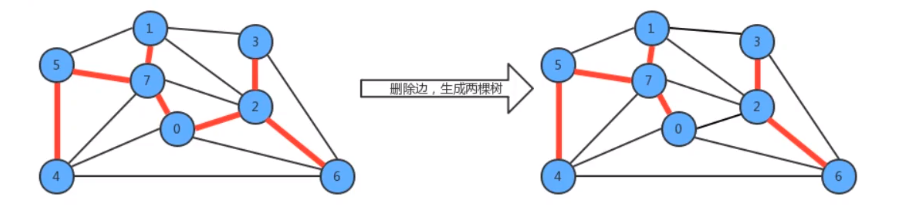
2)切分定理
- 切分
- 横切边
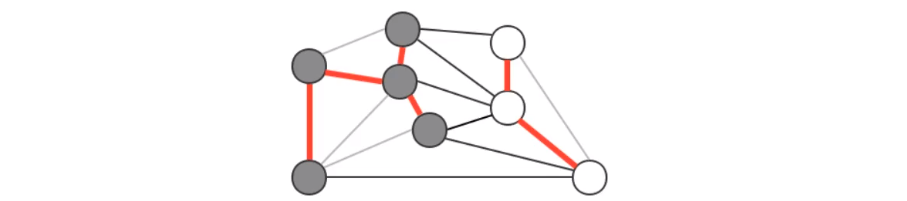
- 切分定理
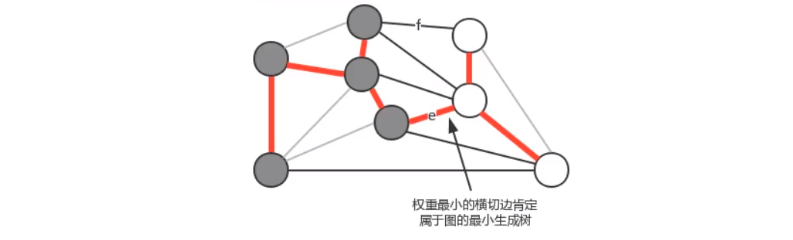
- 注意
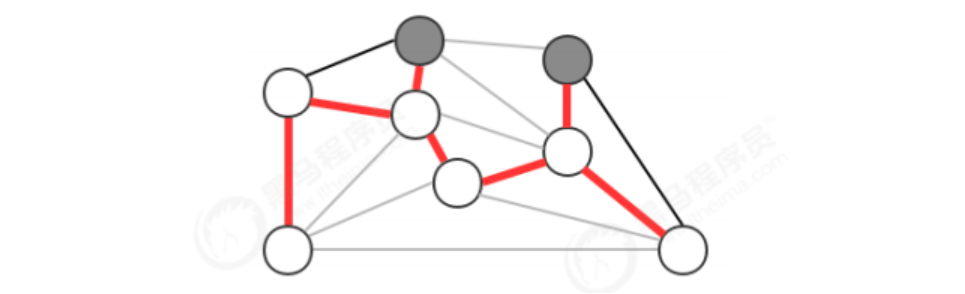
3)贪心算法
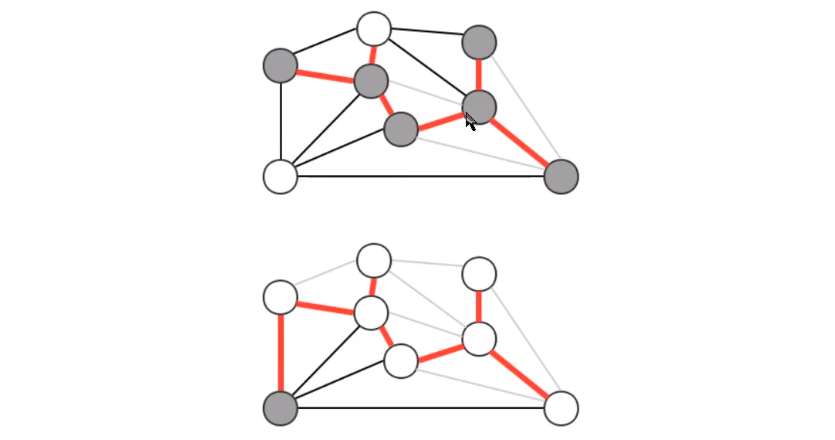
贪心算法是计算图的最小生成树的基础算法,它的基本原理就是 切分定理
使用切分定理找到最小生成树的一条边,不断的重复直到找到最小生成树的所有边
如果图有 v 个顶点,那么需要找到 v-1 条边,就可以表示该图的最小生成树
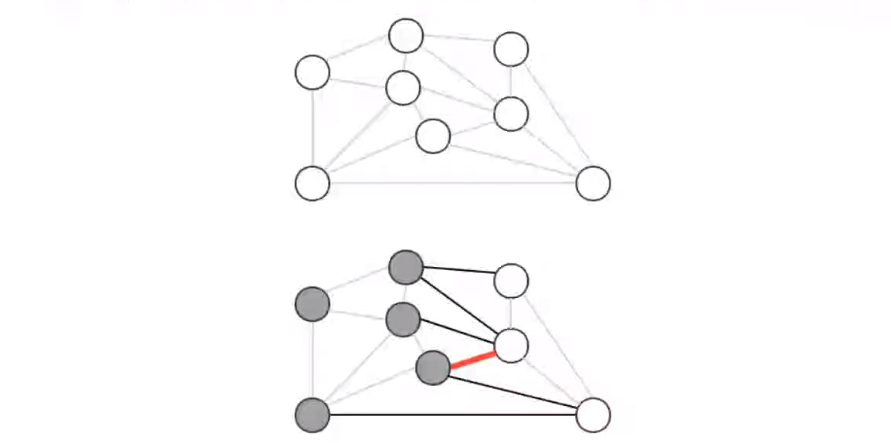
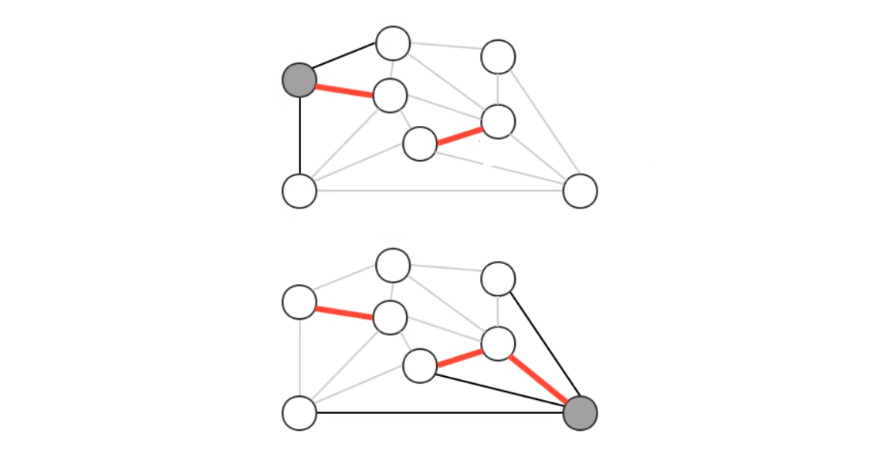
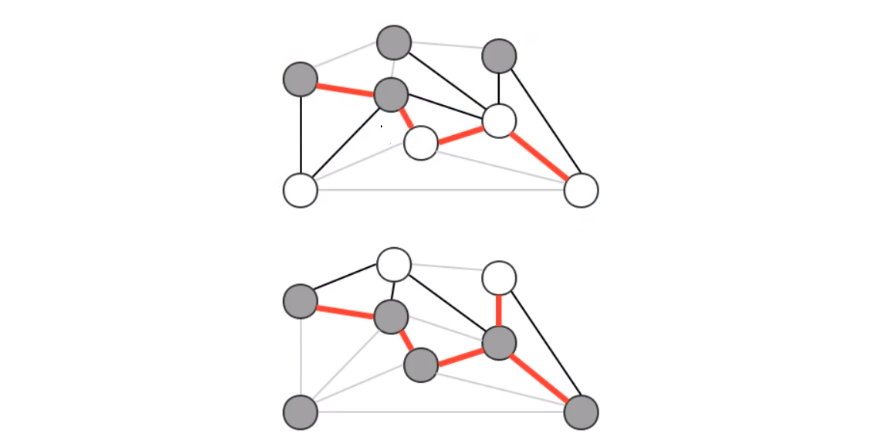
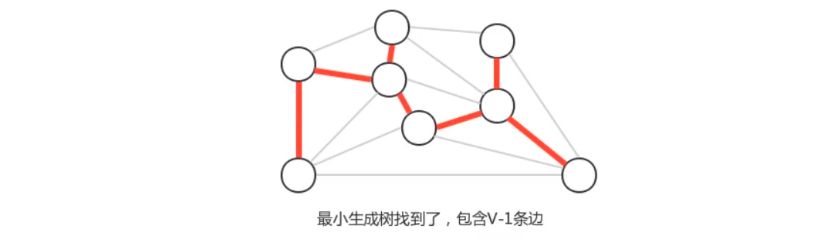
4)prim算法
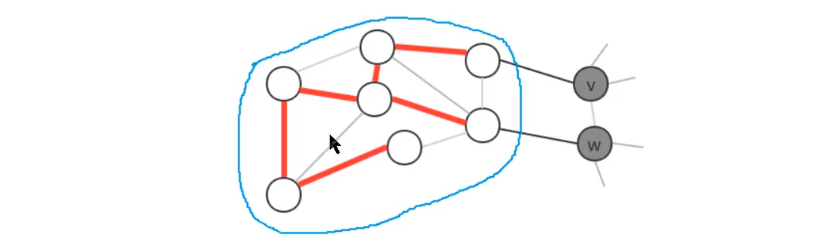
- prim算法的切分规则
1、prim算法api设计
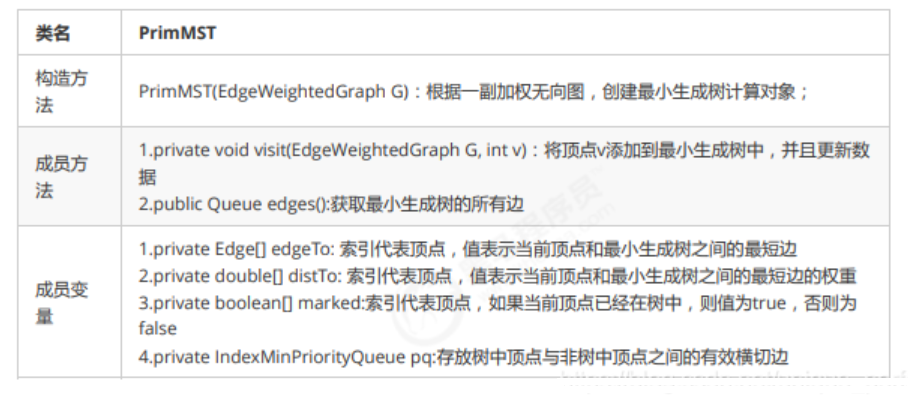
2、prim算法的实现原理
prim算法始终将图中的顶点切分成两个集合,最小生成树顶点 和 非最小生成树顶点,通过不断的重复做某些操作,可以逐渐将非最小生成树中的顶点加入到最小生成树中,直到所有的顶点都加入到最小生成树中
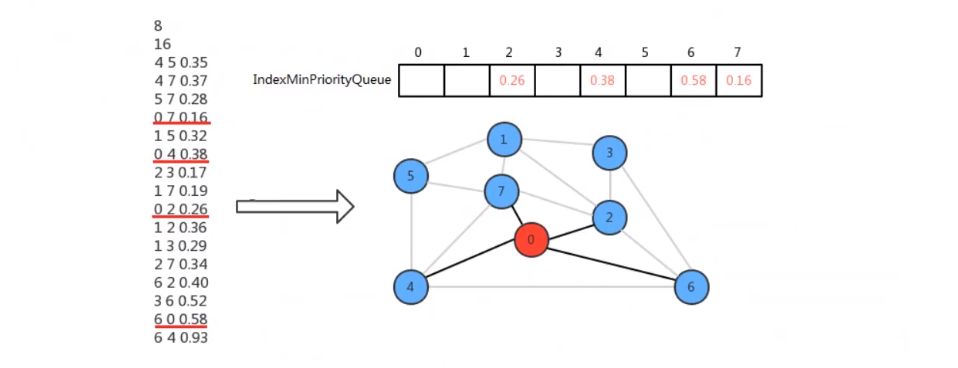
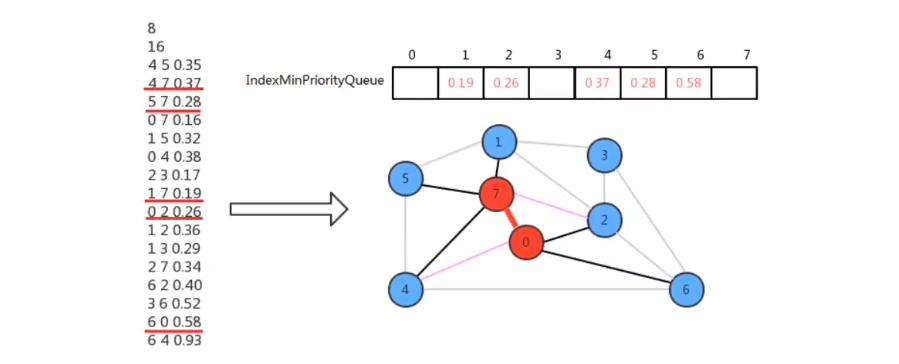
3、代码
package chapter18;
import chapter03.queue;
import chapter07.indexminpriorityqueue;
import chapter17.edge;
import chapter17.edgeweightedgraph;
/**
-
@author 土味儿
-
date 2021/9/17
-
@version 1.0
-
最小生成树prim算法
*/
public class primmst {
/**
-
最小边
-
索引代表顶点
-
值表示当前顶点到最小生成树之间的最小边
*/
private edge[] edgeto;
/**
-
最小边的权重
-
索引代表顶点
-
值表示当前顶点到最小生成树之间的最小边的权重
*/
private double[] distto;
/**
-
索引代表顶点
-
如果当前顶点已经在树中,则值为true,否则为false
*/
private boolean[] marked;
/**
- 存放树中顶点与非树中顶点的有效横切边
*/
private indexminpriorityqueue pq;
/**
-
构造器
-
根据加权无向图创建最小生成树
-
@param g
*/
public primmst(edgeweightedgraph g) {
// 初始化edgeto
this.edgeto = new edge[g.getvnum()];
// 初始化distto
this.distto = new double[g.getvnum()];
for (int i = 0; i < g.getvnum(); i++) {
// 默认值:正无穷大
this.distto[i] = double.positive_infinity;
}
// 初始化marked
this.marked = new boolean[g.getvnum()];
// 初始化pq
pq = new indexminpriorityqueue(g.getvnum());
// 默认让顶点0进入到树中,但是树中只有一个顶点0,因此,顶点0没有和任何顶点相连,所以distto对应位置处的值为0.0
distto[0] = 0.0;
pq.insert(0,0.0);
// 遍历索引最小优先队列,拿到最小横切边对应的顶点,把该顶点加入到最小树中
while(!pq.isempty()){
visit(g, pq.delmin());
}
}
/**
-
获取最小生成树的所有边
-
@return
*/
public queue edges(){
// 创建队列对象
queue alledges = new queue<>();
// 把edgeto中非null的值加入队列
for (int i = 0; i < edgeto.length; i++) {
if(edgeto[i] != null){
alledges.enqueue(edgeto[i]);
}
}
return alledges;
}
/**
-
将顶点v添加到最小生成树中,并更新数据
-
@param g
-
@param v
*/
private void visit(edgeweightedgraph g,int v){
// 把顶点v添加到最小生成树中
marked[v] = true;
// 更新数据
for (edge e : g.adj(v)) {
// 获取边e的另外一个顶点w(当前顶点v)
int w = e.other(v);
// 判断另一个顶点是否在树中,如果在树中,不做处理;如果不在树中,更新数据
if(marked[w]){
// 继续下次循环;不是退出,不能用break
continue;
}
// 比较权重:判断边e的权重是否小于 w到最小树中已存在的最小边的权重
if(e.getweight() < distto[w]){
// 更新数据
edgeto[w] = e;
distto[w] = e.getweight();
if(pq.contains(w)){
pq.changeitem(w, e.getweight());
}else{
pq.insert(w, e.getweight());
}
}
}
}
}
- 测试
package chapter18;
import chapter03.queue;
import chapter17.edge;
import chapter17.edgeweightedgraph;
import org.junit.test;
import java.io.bufferedreader;
import java.io.ioexception;
import java.io.inputstreamreader;
/**
-
@author 土味儿
-
date 2021/9/17
-
@version 1.0
-
测试prim最小生成树
*/
public class primmsttest {
@test
public void test() throws ioexception {
// 准备一幅加权无向图
bufferedreader br = new bufferedreader(new inputstreamreader(primmsttest.class.getclassloader().getresourceasstream(“min_create_tree_test.txt”)));
// 顶点数量
int total = integer.parseint(br.readline());
// 加权无向图
edgeweightedgraph g = new edgeweightedgraph(total);
// 边的数量
int edges = integer.parseint(br.readline());
// 依次读取边
for (int i = 0; i < edges; i++) {
string line = br.readline();
string[] s = line.split(" ");
int v = integer.parseint(s[0]);
int w = integer.parseint(s[1]);
double weight = double.parsedouble(s[2]);
// 创建加权无向边
edge edge = new edge(v, w, weight);
// 向图中加入边
g.addedge(edge);
}
// 创建prim最小生成树对象
primmst primmst = new primmst(g);
// 得到最小生成树
queue alledges = primmst.edges();
// 输出
for (edge e : alledges) {
int x = e.either();
int y = e.other(x);
double w = e.getweight();
system.out.println(x + " - " + y + " : " + w);
}
}
}
- min_create_tree_test.txt
8
16
4 5 0.35
4 7 0.37
5 7 0.28
0 7 0.16
1 5 0.32
0 4 0.38
2 3 0.17
1 7 0.19
0 2 0.26
1 2 0.36
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52

发表评论