【leftchild = parent * 2 + 1】
【rightchild = parent * 2 + 2】
【parent = (child - 1)/2】
- 以上就是它们之间的关系,对于任何的地方都适用
⏳向下调整算法
小根堆调整
- 也就是从根节点开始,作为父亲结点,选出其左右孩子中较小的那一个,若是比父亲结点来的小,则交换这两个结点,然后更新交换后的孩子结点为新的父亲结点,继续向下调整,直到叶子结点就终止
大根堆调整
- 大根堆与小根堆刚好相反。不过一样是从根节点开始,作为父亲结点,选出其左右孩子中较大的那一个,若是比父亲结点来的大,则交换这两个结点,然后更新交换后的孩子结点为新的父亲结点,继续向下调整,直到叶子结点就终止
🐀算法图示
- 以下就是向下调整算法的原理,首先看到27,为根结点,接着我们看起左子树和右子树是不是均为小顶堆
- 然后现在它的左右孩子为15和19,经过比较是15来的小,选出小的那个孩子后,就将其与根节点进行一个比较,若是比根节点小的,则将这个小的孩子换上来,若是比根节点大的,就原本就是小顶锥,就不需要换了
- 然后在换完一次后,上一次的较小孩子结点就成了下一次得的父亲结点,它也会有自己的孩子,看到小的那个为28,所以将27与18进行一个交换
- 最后一次的交换便是父亲结点25与27的交换
- 根据我们前面二叉树的知识,这是呈一个等比数列。若一棵满二叉树树的高度为h,那个结点的个数就为2h - 1 = n,那这里是完全二叉树,后面肯定缺了一些结点,那就是2h - 1 - x= n,减1后在减缺的结点x,但是相比n,它是可忽略的值
- 所以我们可以得到h = log2n + 1 + x,根据这个大o渐进法的规则,算法的常数操作可忽略不计
- 所以可以得出这个向下调整算法要调整的高度为o(logn)也就是其时间复杂度
🐀代码实现与分析
void swap(int& x, int& y)
{
int t = x;
x = y;
y = t;
}
void adjust\_down(int\* a, int n, int root)
{
int parent = root;
int child = parent \* 2 + 1;
while (child < n)
{
//选出左右孩子中小的那一个
if (child + 1 < n && a[child + 1] < a[child])
{ //考虑到右孩子越界的情况
child += 1;
//若右孩子来的小,则更新孩子结点为小的那个
}
//交换父亲节点和小的那个孩子结点
if (a[child] < a[parent]){
swap(a[child], a[parent]);
//重置父亲节点和孩子结点
parent = child;
child = parent \* 2 + 1;
}
else { //若已是小根堆,则不交换
break;
}
}
}
- 外层的while循环控制的就是调整到叶子结点时便不再向下做调整,内部的第一个if分支判断是选出左右孩子中小的那一个,因为我们默认左孩子较小,若时右孩子小一些的话,将其值+1便可,注意这里的child + 1 < n,因为a[child + 1]去算它的右孩子时,就有可能会越界了。因此要加一个条件就是child + 1 < n,当最后的这个叶子结点只落在左孩子上时,我们才去进行一个判断
- 第二个分支判断就是交换父亲结点和小的那个孩子结点,然后进行一个更替,但若是孩子结点这时已经比父亲结点要来的大了,就不需要一直往下调整,已经是ok了,因此直接break就行
⏳建堆
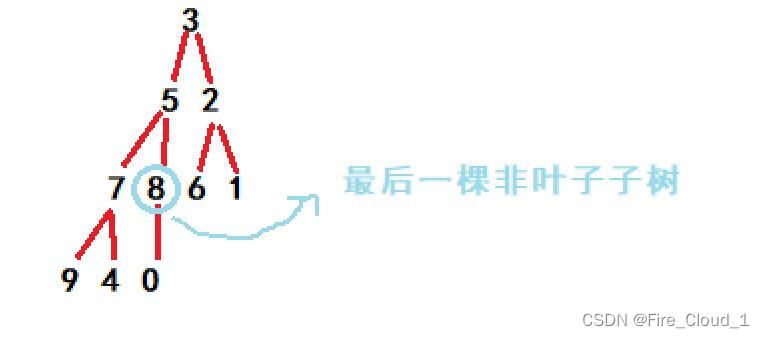
- 那我们应该从哪里开始调整呢,是去调整这个叶子6或者1吗,既然它是叶子,我们就没有必要去进行一个调整,只需要调整子树即可,也就是图中的这个8
- 那我们要怎么去找到8这个结点呢,这就要看它的叶子结点0了,我们上面有说到过一组公式,就是知道一个父亲结点的孩子结点,怎么去求这个父亲结点parent = (child - 1)/2
- 而最后一个结点的值为n - 1,所以我们将其定义为一个循环,从下往上依次去进行一个换位寻找,直到原来的根节点为止,然后内部通过我们上面推导出的【向下调整算法】进行一个改进,变为【向“上”调整算法】
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
adjust\_down(a, n, i);
- 这个叫做自底向上的建堆方式,从倒数第二层的结点(叶子结点得上一层)开始,从右向左,从下到上得向下进行调整
⏳排升序,建大堆or小堆?
- 一般我们都会去实现升序排序,那对于这个升序排序的话是要建大堆呢还是小堆呢?,许多同学可能都会认为是建小堆,因为小堆的话是根结点来的小,也就是开头来的小,那后面大,也就构成了升序排序,真的是这样吗,我们来探究一番?
- 从图示中我们可以看出,若是建小堆的话,那最小的那个数就在堆顶,这个歌时候再去剩下的数里面选数的话,这个根节点就需要重新选择,但是这样的话原本的左孩子结点就会变成新的根结点,而右孩子结点就会变成新的左孩子结点
- 这就会导致剩下的树结构都乱了,那便需要重新去建堆才能选出下一个数,对于建堆,其时间复杂度我们可以看出来,一层for循环,需要o(n),这就会导致堆排序的时间复杂度上升,那也就没了它的优势
- 所以我们在是实现升序排序的时候不要用大根堆,效率过低,并且建堆选数,还不如直接遍历选数,遍历的话也是可以找出最小数
//选出左右孩子中大的那一个
if (child + 1 < n && a[child + 1] > a[child])
{ //考虑到右孩子越界的情况
child += 1;
//若右孩子来的小,则更新孩子结点为小的那个
}
//交换父亲节点和大的那个孩子结点
if (a[child] > a[parent]){
swap(a[child], a[parent]);
//重置父亲节点和孩子结点
parent = child;
child = parent \* 2 + 1;
}
else { //若已是小根堆,则不交换
break;
}
- 也就是修改两个if分支的条件,去找出大的那个孩子结点,找出后若比父亲结点小,则进行一个交换即可
- 下面就是调整出来的大根堆,这个时候我们只需要将根结点的第一个数与最后一个叶子结点进行一个交换即可
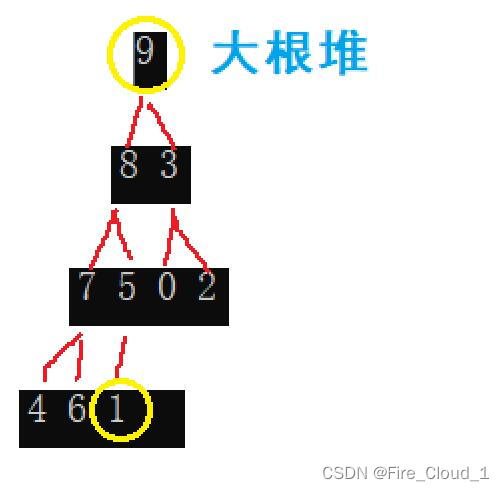
- 那接下来应该怎么办呢?我们将刚刚从堆顶换下来的最大的那个数排除在堆外,接下去看我用绿色笔圈起来的两个子树,依旧是呈现一个大顶堆,这时看到可以看到我们两个紫色三角形做的两个标记数,这就是下一次要交换的两个数,也就是每次都将上层的大的数字与最后层的叶子结点进行一个交换,接着在交换之后将最低端的那个数排除在堆外即可,因为即使排除了这个数字,也不会像上面那样改变了整棵树的整体层次结构,左右子树依旧是呈现一个大顶堆的现状
- 我们再来分析一下其时间复杂度,向下调整的话我们上面说到过是logn,又因为有n个数需要调整,因此建堆的时间复杂度为o(n),所以它的总体时间复杂度为o(nlogn)
//排升序,建大堆
int end = n - 1; //获取最后一个叶子结点
while (end > 0)
{
swap(a[0], a[end]); //将第一个数与最后一个数交换
adjust\_down(a, end, 0); //向下调整,选出次大的数,再和倒数第二个数交换
end--; //最后一个数前移,上一个交换完后的数不看做堆中的数
}
- 首先,你需要去获取最后一个叶子结点的位置,然后建立一个循环,去交换第一个数和最后一个数,接着继续寻找次大的数
- 通过一个【向下调整算法】,去选数,再让每次结束后的end–,也就是往左结点遍历,直到遍历到这个根结点为止,才跳出while循环
⏳总体时间复杂度分析【⭐⭐⭐⭐⭐】
向下调整算法
- 对于向下调整算法,可以看出,它是通过一个外层的while循环在控制,慢慢地向下遍历,若是小根堆调整,则是将小的结点都慢慢交换上来,大根堆则是相反
- 从第0个结点也就是根节点开始到第n - 1个结点,就是有n个结点,因此其时间复杂度为o(n)
建堆
- 对于建堆的操作,虽然只有两行,一个for循环内部嵌套一个向下调整算法,大家可能认为这是o(n)或是o(n2),不是很确定,我们一起来看看👀
- 上面说过,对于这个建堆,是一个自底向上的方式,从右到左,从下到上进行一个调整
- 我们现在假设其为一棵满二叉树,堆高为h。同样的,假设每层得高度为hi,每层的结点数为ni,则建堆得复杂度为t(n) =
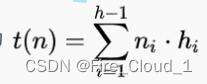
- 我们根据一棵满二叉树去推导,用它得这个结点个数*最多调整次数,就可以一步步推算出下面的这个公式
- 然后从这个公式我们可以观察出此为一个等比数列,所以我们可以联想到等比数列得应用中比较常见的一种叫做【错位相减法】
- 让原本的公式两遍都去乘以2,然后将其后移,实施一个错位相减,后面经过归类,用等比数列的公式去套,就可以得出t(n)是为-h + 2h-1
- 我们在上面有说到过这个二叉树的总结点个数公式为2h-1 = n,而对于树的高度,就是我们在向下调整算法时说到的最多调整logn次
- 所以可以得出这个整体的时间复杂度为n - logn,再由这个大o渐进法的规则,保留高阶次的复杂度,最后可以看出这个建堆的总体时间复杂度化简后为为o(n)
排序
- 最后呢是通过建大堆去实现这个升序排序。首先上面的建堆算法是o(n),然后剩下的部分我们通过向下调整算法选数,为o(logn)
- 所以可以得出堆排序的完整时间复杂度应该是为o(nlogn)
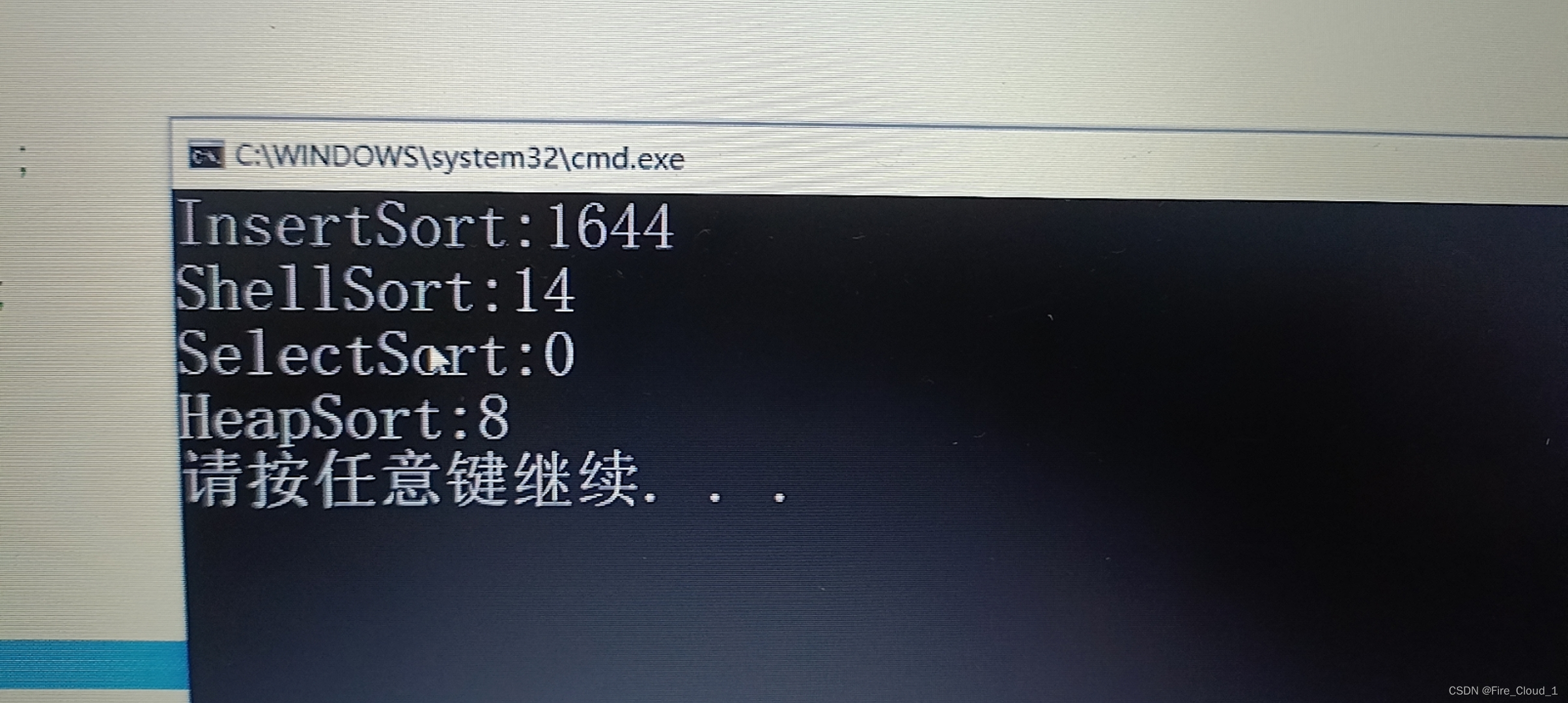
- 可以看出,这个堆排序的效率还是很高的,和希尔排序是一个层次级别,不过8ms和14ms差别不大,但可以看出,比直接插入排序是快了不少。大家也可以自己去测试一下💻
// 测试排序的性能对比
void testop()
{
srand(time(0));
const int n = 100000;
int\* a1 = (int\*)malloc(sizeof(int) \* n);
int\* a2 = (int\*)malloc(sizeof(int) \* n);
int\* a3 = (int\*)malloc(sizeof(int) \* n);
int\* a4 = (int\*)malloc(sizeof(int) \* n);
int\* a5 = (int\*)malloc(sizeof(int) \* n);
int\* a6 = (int\*)malloc(sizeof(int) \* n);
for (int i = 0; i < n; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
}
int begin1 = clock();
insertsort2(a1, n);
int end1 = clock();
int begin2 = clock();
shell\_sort2(a2, n);
int end2 = clock();
int begin3 = clock();
//selectsort(a3, n);
int end3 = clock();
int begin4 = clock();
heap\_sort(a4, n);
int end4 = clock();
int begin5 = clock();
//quicksort(a5, 0, n - 1);
int end5 = clock();
int begin6 = clock();
//mergesort(a6, n);
int end6 = clock();
printf("insertsort:%d\n", end1 - begin1);
printf("shellsort:%d\n", end2 - begin2);
// printf("selectsort:%d\n", end3 - begin3);
printf("heapsort:%d\n", end4 - begin4);
//printf("quicksort:%d\n", end5 - begin5);
//printf("mergesort:%d\n", end6 - begin6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);

**既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上大数据知识点,真正体系化!**
**由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新**
**[需要这份系统化资料的朋友,可以戳这里获取](https://bbs.csdn.net/topics/618545628)**
in6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
[外链图片转存中...(img-px6k8khy-1714519107034)]
[外链图片转存中...(img-ewguz6qi-1714519107034)]
[外链图片转存中...(img-83xx3qyq-1714519107034)]
**既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上大数据知识点,真正体系化!**
**由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新**
**[需要这份系统化资料的朋友,可以戳这里获取](https://bbs.csdn.net/topics/618545628)**


发表评论