目录
1.分治概念
任何可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小,解题所需的计算时间往往也越少,从而也较容易处理。例如,对于n个元素的排序问题,当n=1时,不需任何计算;n=2时,只要做一次比较即可排好序;n=3时只要进行两次比较即可;...而当n较大时,问题就不那么容易处理了。要想直接解决一个较大的问题,有时是相当困难的。
分治法的设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破分而治之。如果原问题可分割成k个子问题,1<k≤n,且这些子问题都可解,并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小规模模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易求出其解。由此自然导致递归算法。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
把大规模变成小规模,不是将问题缩小!
2.递归的概念递归:
若一个函数直接地或间接地调用自己,则称这个函数是递归的函数。(简单地描述为"自己调用自己")
不要使用间接递归,因为间接递归很难处理,难于调试
3.分治策略的:
1.分治策略的特征:
分治法所能解决的问题一般具有以下四个特征:
该问题的规模缩小到一定的程度就可以容易地解决。
该问题可以分解为若干个规模较小的相同问题。
使用小规模的解,可以合并成,该问题原规模的解。
该问题所分解出的各个子规模是相互独立的。
2.分治法步骤:
在分治策略中递归地求解一个问题,在每层递归中应用如下三个步骤:
分解:将问题划分成一些子问题,子问题的形式与原问题一样,只是规模更小。
解决:递归地求解子问题。如果子问题的规模足够小,则停止递归,直接求解。
合并:将小规模的解组合成原规模问题的解。
4.栈的面试题:
5.示例:
1.示例1求解n的阶乘
注意:不考虑int溢出
2.阶乘可递归的定义为:
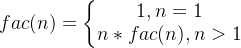
3.递归程序:
int fun(int n)
{
int sum = 1;
for (int i = 1; i<=n; ++i)
{
sum = sum * i;
}
return sum;
}
int fac(int n)
{
if (n<=1)
return 1;
else
return fac(n - 1) * n;
}
int main()
{
printf("%d",fun(6));
printf("%d",fac(5));
return 0;
}
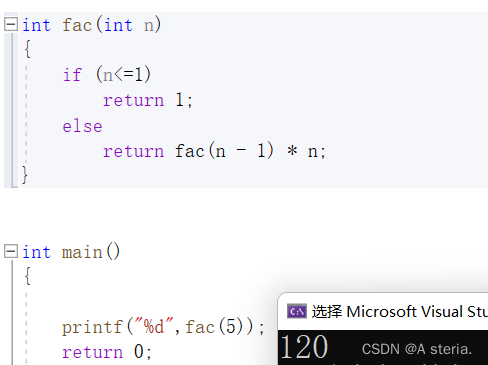
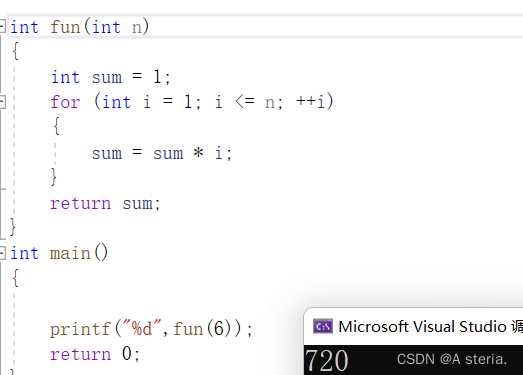
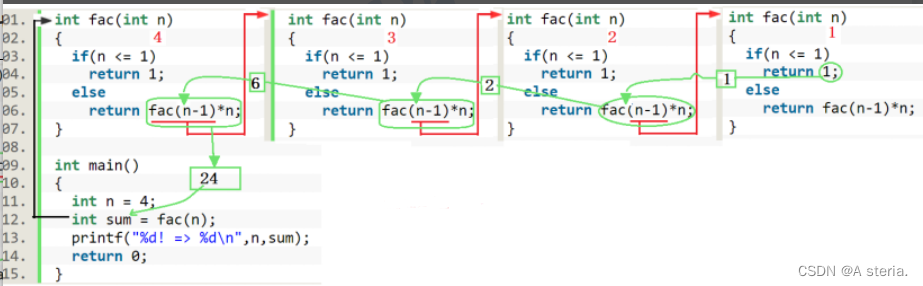
4.图解递归过程(代码的调动过程)
5.图解递归过程(栈帧的动态调动过程)

6.总结
函数被调用,不管是自己调用自己,还是被其它函数调用,都将会给被调用函数分配栈帧。不存在无穷递归。即递归函数必须要有一个是递归结束的出口(要有递归中止的条件语句)。问题的规模不要过大,递归过深,引起栈溢出。
2.实例2:fibonacci
无穷数列1,1,2,3,5,8,13,21,34,55,......,称为fibonacci数列计算第n位数列。
1.分析:
2.递归定义:
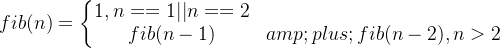
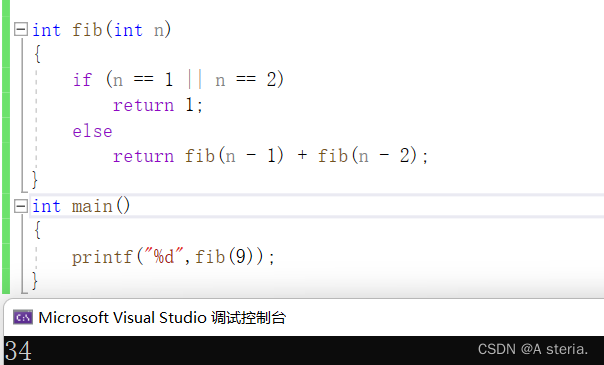
3.递归程序:
int fib(int n)
{
if (n == 1 || n == 2)
return 1;
else
return fib(n - 1) + fib(n - 2);
} 
4.非递归程序:
int fib(int n)
{
int a = 1, b = 1, c = 1;
//if (n == 1 || n == 2) return 1;
for (int i = 3; i <= n; ++i)
{
c = a + b;
a = b;
b = c;
}
return c;
}5.时间复杂度分析:
o(n)(非递归)
o(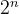 )(递归)
)(递归)
6.程序优化:
int fibon(int n,int a,int b)
{
if(n==1||n==2)
return a;
else
return fibon(n-1,a+b,a);
}
int fibon(int n)
{
int a=1,b=1;
return fac(n,a,b);
}6.练习
1.非递归代码,使用迭代
void printint(int n)
{
while (n != 0)
{
printf("%u ", n % 10);
n = n / 10;
}
}
int main()
{
printint(12345);
}
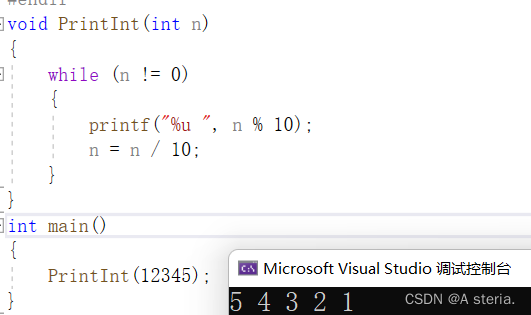
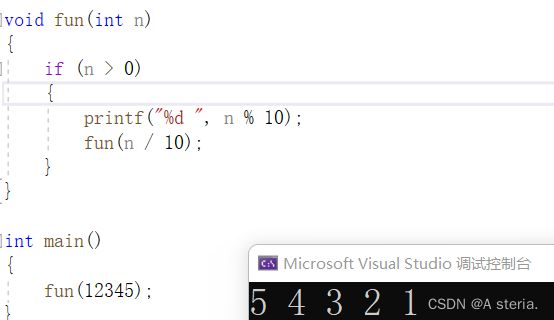
2.递归:
void fun(int n)
{
if (n > 0)
{
printf("%d ", n % 10);
fun(n / 10);
}
}
int main()
{
fun(12345);
}
void fun(int n)
{
if (n > 0)
{
fun(n / 10);
printf("%d ", n % 10);
}
}
int main()
{
fun(12345);
}
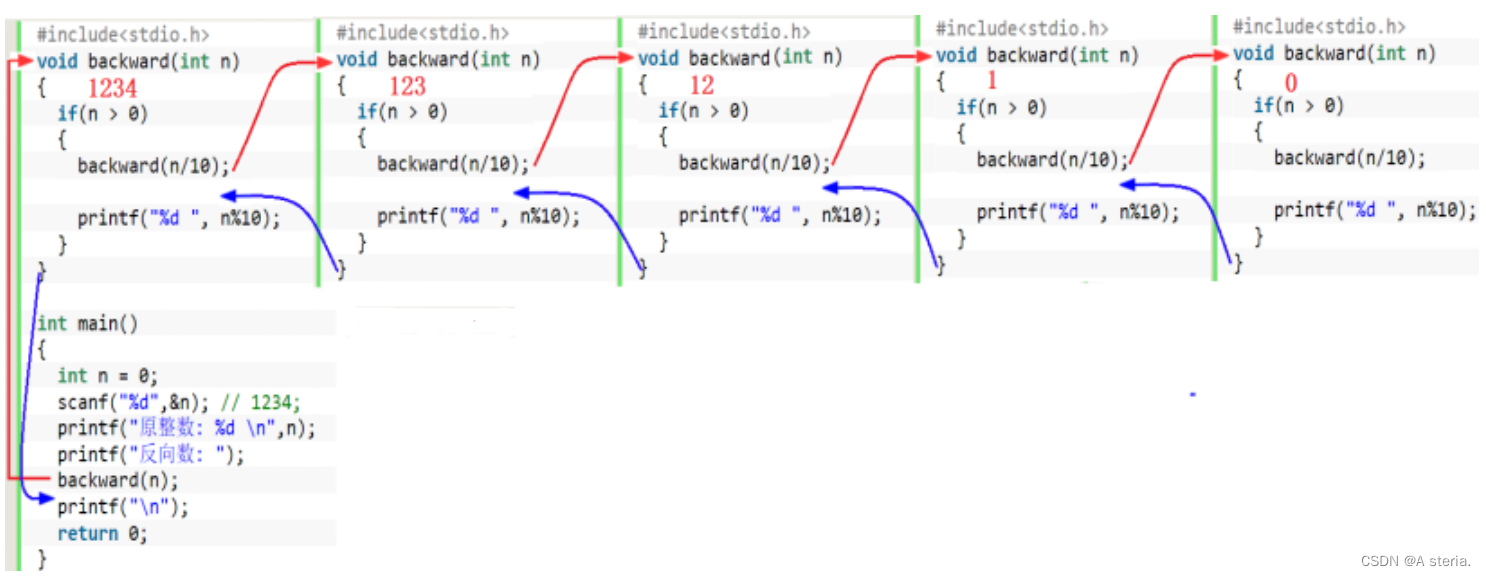
3.调用过程分析:
4.总结:
求余数总是取当前整数的最后一位,所以先输出余数后递归可实现倒序输出;
如果先递归后输出玉树,则是在回归的过程中输出,实现的就是正序输出。

发表评论