扩散模型 (Diffusion Model) 简要介绍与源码分析

扩散模型 (diffusion model) 简要介绍与源码分析

前言

近期同事分享了 diffusion model, 这才发现生成模型的发展已经到了如此惊人的地步, openai 推出的 dall-e 2 可以根据文本描述生成极为逼真的图像, 质量之高直让人惊呼哇塞. 今早公众号给我推送了一篇关于 stability ai 公司的报道, 他们推出的 ai 文生图扩散模型 stable diffusion 已开源, 能够在消费级显卡上实现 dall-e 2 级别的图像生成, 效率提升了 30 倍.

于是找到他们的开源产品体验了一把, 在线体验地址在 https://huggingface.co/spaces/stabilityai/stable-diffusion (开源代码在 github 上: https://github.com/compvis/stable-diffusion), 在搜索框中输入 “a dog flying in the sky” (一只狗在天空飞翔), 生成效果如下:

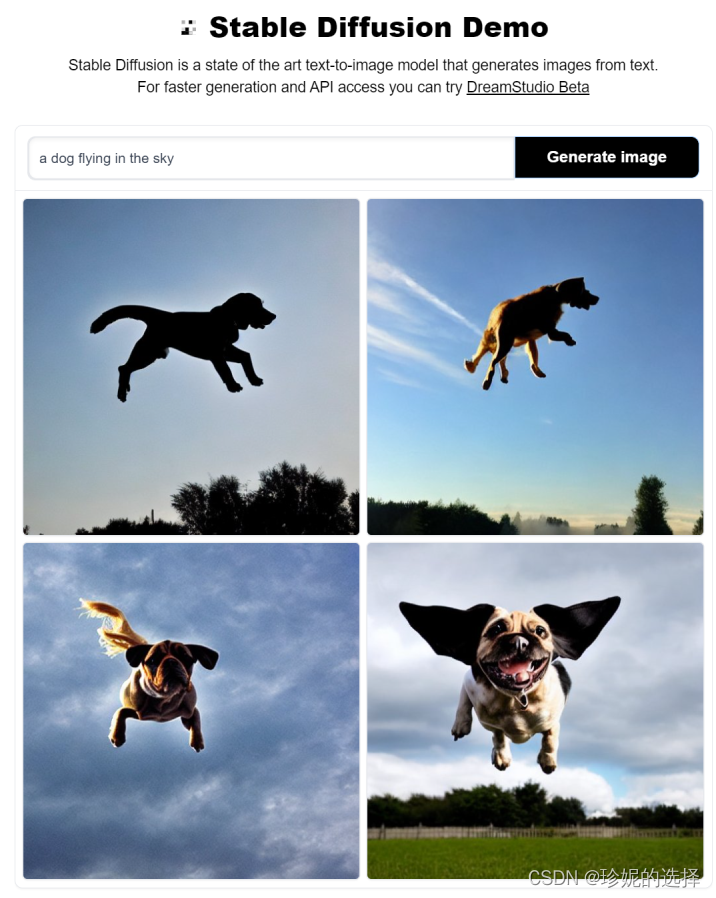
amazing! 当然, 不是每一张图片都符合预期, 但好在可以生成无数张图片, 其中总有效果好的. 在震惊之余, 不免对 diffusion model (扩散模型) 背后的原理感兴趣, 就想看看是怎么实现的.

当时同事分享时, ppt 上那一堆堆公式扑面而来, 把我给整懵圈了, 但还是得撑起下巴, 表现出似有所悟、深以为然的样子, 在讲到关键处不由暗暗点头以表示理解和赞许. 后面花了个周末专门学习了一下, 公式推导+代码分析, 感觉终于了解了基本概念, 于是记录下来形成此文, 不敢说自己完全懂了, 毕竟我不做这个方向, 但回过头去看 ppt 上的公式就不再发怵了.

广而告之

可以在微信中搜索 “珍妮的算法之路” 或者 “world4458” 关注我的微信公众号, 可以及时获取最新原创技术文章更新.

另外可以看看知乎专栏 poormemory-机器学习, 以后文章也会发在知乎专栏中.

总览

本文对 diffusion model 扩散模型的原理进行简要介绍, 然后对源码进行分析. 扩散模型的实现有多种形式, 本文关注的是 ddpm (denoising diffusion probabilistic models). 在介绍完基本原理后, 对作者释放的 tensorflow 源码进行分析, 加深对各种公式的理解.

参考文章

在理解扩散模型的路上, 受到下面这些文章的启发, 强烈推荐阅读:

• lilian 的博客, 内容非常非常详实, 干货十足, 而且每篇文章都极其用心, 向大佬学习: what are diffusion models?
• ewrfcas 的知乎, 公式推导补充了更多的细节: 由浅入深了解diffusion model
• lilian 的博客, 介绍变分自动编码器 vae: from autoencoder to beta-vae, diffusion model 需要从分布中随机采样样本, 该过程无法求导, 需要使用到 vae 中介绍的重参数技巧.
• denoising diffusion probabilistic models 论文,
  • 其 tf 源码位于: https://github.com/hojonathanho/diffusion, 源码介绍以该版本为主
  • pytorch 的开源实现: https://github.com/lucidrains/denoising-diffusion-pytorch, 核心逻辑和上面 tensorflow 版本是一致的, stable diffusion 参考的是 pytorch 版本的代码.

扩散模型介绍

基本原理

diffusion model (扩散模型) 是一类生成模型, 和 vae (variational autoencoder, 变分自动编码器), gan (generative adversarial network, 生成对抗网络) 等生成网络不同的是, 扩散模型在前向阶段对图像逐步施加噪声, 直至图像被破坏变成完全的高斯噪声, 然后在逆向阶段学习从高斯噪声还原为原始图像的过程.

具体来说, 前向阶段在原始图像 ${\mathbf{x}}_0$ 上逐步增加噪声, 每一步得到的图像 ${\mathbf{x}}_t$ 只和上一步的结果 ${\mathbf{x}}_{t-1}$ 相关, 直至第 $t$ 步的图像 ${\mathbf{x}}_t$ 变为纯高斯噪声. 前向阶段图示如下:

而逆向阶段则是不断去除噪声的过程, 首先给定高斯噪声 ${\mathbf{x}}_t$, 通过逐步去噪, 直至最终将原图像 ${\mathbf{x}}_0$ 给恢复出来, 逆向阶段图示如下:

模型训练完成后, 只要给定高斯随机噪声, 就可以生成一张从未见过的图像. 下面分别介绍前向阶段和逆向阶段, 只列出重要公式,

前向阶段

由于前向过程中图像 ${\mathbf{x}}_t$ 只和上一时刻的 ${\mathbf{x}}_{t-1}$ 有关, 该过程可以视为马尔科夫过程, 满足:

$$\begin{array}{rl}q\left(x_{1:t}\mid x_0\right)& =\prod _{t=1}^{t}q\left(x_t\mid x_{t-1}\right)\\ q\left(x_t\mid x_{t-1}\right)& =\mathcal{n}\left(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{i}\right),\end{array}$$

其中 ${\beta }_t\in (0,1)$ 为高斯分布的方差超参, 并满足 ${\beta }_1<{\beta }_2<\dots <{\beta }_t$. 另外公式 (2) 中为何均值 $x_{t-1}$ 前乘上系数 $\sqrt{1-{\beta }_t}{x}_{t-1}$ 的原因将在后面的推导介绍. 上述过程的一个美妙性质是我们可以在任意 time step 下通过 重参数技巧 采样得到 $x_t$.

重参数技巧 (reparameterization trick) 是为了解决随机采样样本这一过程无法求导的问题. 比如要从高斯分布 $z\sim \mathcal{n}(z;\mu ,{\sigma }^2\mathbf{i})$ 中采样样本 $z$, 可以通过引入随机变量 $ϵ\sim \mathcal{n}(0,\mathbf{i})$, 使得 $z=\mu +\sigma \odot ϵ$, 此时 $z$ 依旧具有随机性, 且服从高斯分布 $\mathcal{n}(\mu ,{\sigma }^2\mathbf{i})$, 同时 $\mu$ 与 $\sigma$ (通常由网络生成) 可导.

简要了解了重参数技巧后, 再回到上面通过公式 (2) 采样 $x_t$ 的方法, 即生成随机变量 ${ϵ}_t\sim \mathcal{n}(0,\mathbf{i})$,
然后令 ${\alpha }_t=1-{\beta }_t$, 以及 $\overline{{\alpha }_t}={\prod }_{i=1}^t{\alpha }_t$, 从而可以得到:

$$\begin{array}{rl}{x}_t& =\sqrt{1-{\beta }_t}{x}_{t-1}+{\beta }_t{ϵ}_1\text{ where }{ϵ}_1,{ϵ}_2,\dots \sim \mathcal{n}(0,\mathbf{i}),\text{reparameter trick};\\ & =\sqrt{a_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_1\\ & =\sqrt{a_t}\left(\sqrt{a_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_2\right)+\sqrt{1-{\alpha }_t}{ϵ}_1\\ & =\sqrt{a_t{a}_{t-1}}{x}_{t-2}+\left(\sqrt{a_t\left(1-{\alpha }_{t-1}\right)}{ϵ}_2+\sqrt{1-{\alpha }_t}{ϵ}_1\right)\\ & =\sqrt{a_t{a}_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{ϵ}}_2\text{ where }{\overline{ϵ}}_2\sim \mathcal{n}(0,\mathbf{i});\\ & =\dots \\ & =\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{\overline{ϵ}}_t.\end{array}\text{\hspace{1em}(3-1)(3-2)}$$

其中公式 (3-1) 到公式 (3-2) 的推导是由于独立高斯分布的可见性, 有 $\mathcal{n}\left(0,{\sigma }_1^2\mathbf{i}\right)+\mathcal{n}\left(0,{\sigma }_2^2\mathbf{i}\right)\sim \mathcal{n}\left(0,\left({\sigma }_1^2+{\sigma }_2^2\right)\mathbf{i}\right)$, 因此:

$$\begin{array}{rl}& \sqrt{a_t\left(1-{\alpha }_{t-1}\right)}{ϵ}_2\sim \mathcal{n}\left(0,a_t\left(1-{\alpha }_{t-1}\right)\mathbf{i}\right)\\ & \sqrt{1-{\alpha }_t}{ϵ}_1\sim \mathcal{n}\left(0,\left(1-{\alpha }_t\right)\mathbf{i}\right)\\ & \sqrt{a_t\left(1-{\alpha }_{t-1}\right)}{ϵ}_2+\sqrt{1-{\alpha }_t}{ϵ}_1\sim \mathcal{n}\left(0,\left[{\alpha }_t\left(1-{\alpha }_{t-1}\right)+\left(1-{\alpha }_t\right)\right]\mathbf{i}\right)\\ & =\mathcal{n}\left(0,\left(1-{\alpha }_t{\alpha }_{t-1}\right)\mathbf{i}\right).\end{array}$$

注意公式 (3-2) 中 ${\overline{ϵ}}_2\sim \mathcal{n}(0,\mathbf{i})$, 因此还需乘上 $\sqrt{1-{\alpha }_t{\alpha }_{t-1}}$. 从公式 (3) 可以看出

$$\begin{array}{r}q\left(x_t\mid x_0\right)=\mathcal{n}\left(x_t;\sqrt{{\bar{a}}_t}{x}_0,\left(1-{\bar{a}}_t\right)\mathbf{i}\right)\end{array}$$

注意由于 ${\beta }_t\in (0,1)$ 且 ${\beta }_1<\dots <{\beta }_t$, 而 ${\alpha }_t=1-{\beta }_t$, 因此 ${\alpha }_t\in (0,1)$ 并且有 ${\alpha }_1>\dots >{\alpha }_t$, 另外由于 ${\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_t$, 因此当 $t\to \infty$ 时, ${\bar{\alpha }}_t\to 0$ 以及 $(1-{\bar{a}}_t)\to 1$, 此时 $x_t\sim \mathcal{n}(0,\mathbf{i})$. 从这里的推导来看, 在公式 (2) 中的均值 $x_{t-1}$ 前乘上系数 $\sqrt{1-{\beta }_t}{x}_{t-1}$ 会使得 $x_t$ 最后收敛到标准高斯分布.

逆向阶段

前向阶段是加噪声的过程, 而逆向阶段则是将噪声去除, 如果能得到逆向过程的分布 $q\left(x_{t-1}\mid x_t\right)$, 那么通过输入高斯噪声 $x_t\sim \mathcal{n}(0,\mathbf{i})$, 我们将生成一个真实的样本. 注意到当 ${\beta }_t$ 足够小时, $q\left(x_{t-1}\mid x_t\right)$ 也是高斯分布, 具体的证明在 ewrfcas 的知乎文章: 由浅入深了解diffusion model 推荐的论文中: on the theory of stochastic processes, with particular reference to applications. 我大致看了一下, 哈哈, 没太看明白, 不过想到这个不是我关注的重点, 因此 pass. 由于我们无法直接推断 $q\left(x_{t-1}\mid x_t\right)$, 因此我们将使用深度学习模型 $p_{\theta }$ 去拟合分布 $q\left(x_{t-1}\mid x_t\right)$, 模型参数为 $\theta$:

$$\begin{array}{rl}{p}_{\theta }\left(x_{0:t}\right)& =p\left(x_t\right)\prod _{t=1}^t{p}_{\theta }\left(x_{t-1}\mid x_t\right)\\ p_{\theta }\left(x_{t-1}\mid x_t\right)& =\mathcal{n}\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\sigma }_{\theta }\left(x_t,t\right)\right)\end{array}$$

注意到, 虽然我们无法直接求得 $q\left(x_{t-1}\mid x_t\right)$ (注意这里是 $q$ 而不是模型 $p_{\theta }$), 但在知道 $x_0$ 的情况下, 可以通过贝叶斯公式得到 $q\left(x_{t-1}\mid x_t,x_0\right)$ 为:

$$\begin{array}{rl}q\left(x_{t-1}\mid x_t,x_0\right)& =\mathcal{n}\left(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_t\mathbf{i}\right)\end{array}$$

推导过程如下:

$$\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ & \propto \exp (-\frac{1}{2}(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\left)\right)\\ & =\exp (-\frac{1}{2}(\frac{x_t^2-2\sqrt{{\alpha }_t}{x}_t{x}_{t-1}+{\alpha }_t{x}_{t-1}^2}{{\beta }_t}+\frac{x_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{x}_{t-1}+{\bar{\alpha }}_{t-1}{x}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}\left)\right)\\ & =\exp (-\frac{1}{2}(\underset{x_{t-1}\text{ 方差 }}{(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})x_{t-1}^2}-\underset{x_{t-1}\text{ 均值 }}{(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)x_{t-1}}+\underset{\text{与 }{x}_{t-1}\text{ 无关 }}{c(x_t,x_0)}\left)\right)\end{array}$$

上面推导过程中, 通过贝叶斯公式巧妙的将逆向过程转换为前向过程, 且最终得到的概率密度函数和高斯概率密度函数的指数部分 $\exp \left(-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right)=\exp \left(-\frac{1}{2}\left(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}\right)\right)$ 能对应, 即有:

$$\begin{array}{rl}{\tilde{\beta }}_t& =1/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})=1/(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})})=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ {\tilde{\mu }}_t(x_t,x_0)& =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})\\ & =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0\end{array}$$

通过公式 (8) 和公式 (9), 我们能得到 $q\left(x_{t-1}\mid x_t,x_0\right)$ (见公式 (7)) 的分布. 此外由于公式 (3) 揭示的 $x_t$ 和 $x_0$ 之间的关系: $x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{\overline{ϵ}}_t$, 可以得到

$$\begin{array}{r}{x}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\end{array}$$

代入公式 (9) 中得到:

$$\begin{array}{rl}{\tilde{\mu }}_t& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\\ & =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t)\end{array}$$

补充一下公式 (11) 的详细推导过程:

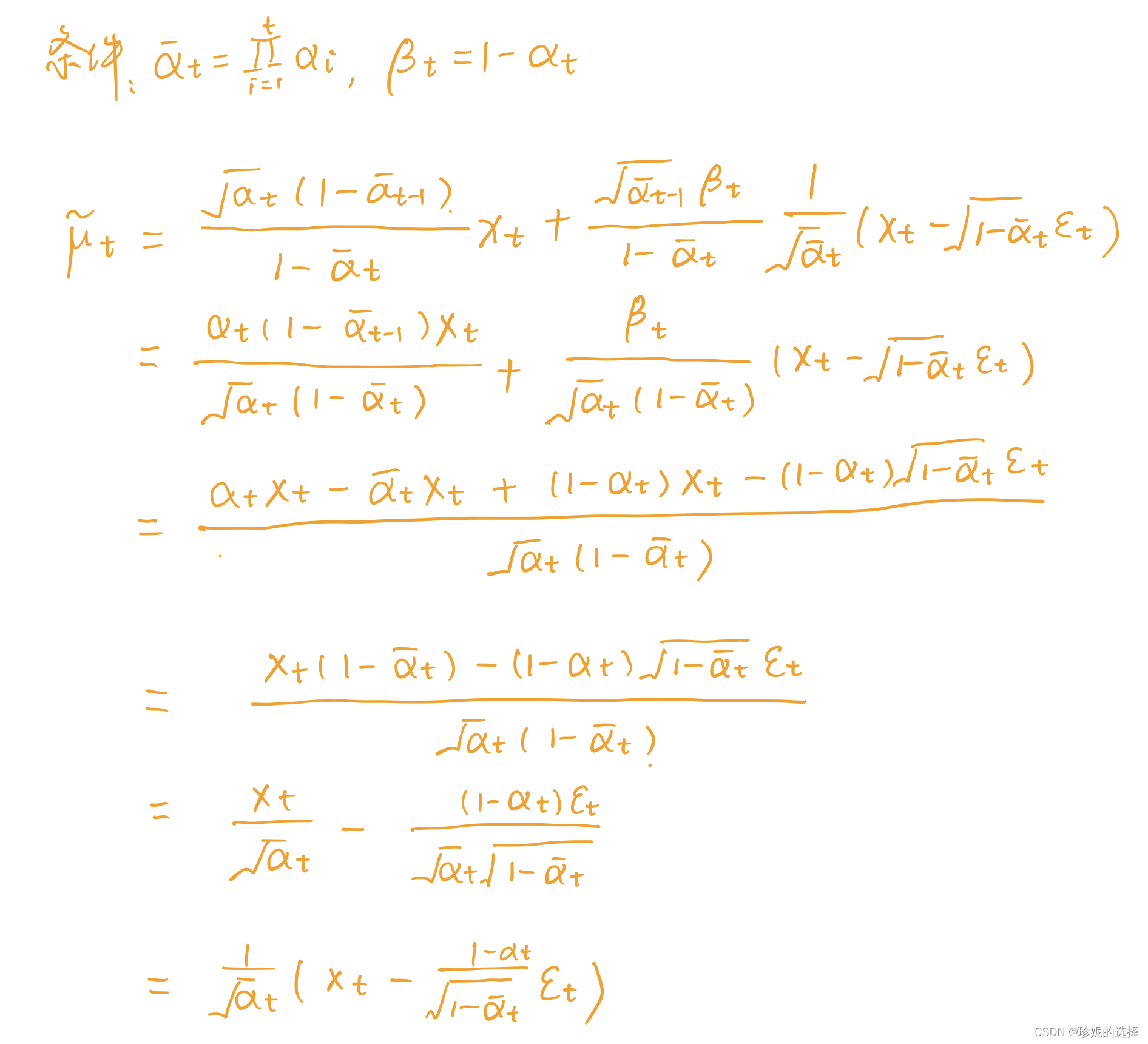
前面说到, 我们将使用深度学习模型 $p_{\theta }$ 去拟合逆向过程的分布 $q\left(x_{t-1}\mid x_t\right)$, 由公式 (6) 知 $p_{\theta }\left(x_{t-1}\mid x_t\right)=\mathcal{n}\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\sigma }_{\theta }\left(x_t,t\right)\right)$, 我们希望训练模型 ${\mu }_{\theta }\left(x_t,t\right)$ 以预估 ${\tilde{\mu }}_t=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t)$. 由于 $x_t$ 在训练阶段会作为输入, 因此它是已知的, 我们可以转而让模型去预估噪声 ${ϵ}_t$, 即令:

$$\begin{array}{rl}{\mu }_{\theta }(x_t,t)& =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))\\ \text{thus }{x}_{t-1}& =\mathcal{n}(x_{t-1};\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t)),{\mathbf{\sigma }}_{\theta }(x_t,t))\end{array}$$

模型训练

前面谈到, 逆向阶段让模型去预估噪声 ${ϵ}_{\theta }(x_t,t)$, 那么应该如何设计 loss 函数 ? 我们的目标是在真实数据分布下, 最大化模型预测分布的对数似然, 即优化在 $x_0\sim q(x_0)$ 下的 $p_{\theta }(x_0)$ 交叉熵:

$$\begin{array}{r}\mathcal{l}={\mathbb{e}}_{q(x_0)}\left[-\log p_{\theta }(x_0)\right]\end{array}$$

和 变分自动编码器 vae 类似, 使用 variational lower bound 来优化: $-\log p_{\theta }(x_0)$ :

$$\begin{array}{rl}-\log p_{\theta }\left(x_0\right)& \le -\log p_{\theta }\left(x_0\right)+d_{kl}\left(q\left(x_{1:t}\mid x_0\right)\Vert p_{\theta }\left(x_{1:t}\mid x_0\right)\right);\text{注: 注意kl散度非负}\\ & =-\log p_{\theta }\left(x_0\right)+{\mathbb{e}}_{q\left(x_{1:t}\mid x_0\right)}\left[\log \frac{q\left(x_{1:t}\mid x_0\right)}{p_{\theta }\left(x_{0:t}\right)/p_{\theta }\left(x_0\right)}\right];\text{ where }{p}_{\theta }\left(x_{1:t}\mid x_0\right)=\frac{p_{\theta }\left(x_{0:t}\right)}{p_{\theta }\left(x_0\right)}\\ & =-\log p_{\theta }\left(x_0\right)+{\mathbb{e}}_{q\left(x_{1:t}\mid x_0\right)}[\log \frac{q\left(x_{1:t}\mid x_0\right)}{p_{\theta }\left(x_{0:t}\right)}+\underset{\text{与q无关 }}{\log p_{\theta }\left(x_0\right)}]\\ & ={\mathbb{e}}_{q\left(x_{1:t}\mid x_0\right)}\left[\log \frac{q\left(x_{1:t}\mid x_0\right)}{p_{\theta }\left(x_{0:t}\right)}\right].\end{array}$$

对公式 (15) 左右两边取期望 ${\mathbb{e}}_{q(x_0)}$, 利用到重积分中的 fubini 定理 可得:

$${\mathcal{l}}_{vlb}=\underset{\text{fubini定理 }}{{\mathbb{e}}_{q\left(x_0\right)}\left({\mathbb{e}}_{q\left(x_{1:t}\mid x_0\right)}\left[\log \frac{q\left(x_{1:t}\mid x_0\right)}{p_{\theta }\left(x_{0:t}\right)}\right]\right)={\mathbb{e}}_{q\left(x_{0:t}\right)}\left[\log \frac{q\left(x_{1:t}\mid x_0\right)}{p_{\theta }\left(x_{0:t}\right)}\right]}\ge {\mathbb{e}}_{q\left(x_0\right)}\left[-\log p_{\theta }\left(x_0\right)\right]$$

因此最小化 ${\mathcal{l}}_{vlb}$ 就可以优化公式 (14) 中的目标函数. 之后对 ${\mathcal{l}}_{vlb}$ 做进一步的推导, 这部分的详细推导见上面的参考文章, 最终的结论是:

$$\begin{array}{rl}{\mathcal{l}}_{vlb}& =l_t+l_{t-1}+\dots +l_0\\ l_t& =d_{kl}\left(q(x_t|x_0)||p_{\theta }(x_t)\right)\\ l_t& =d_{kl}\left(q(x_t|x_{t+1},x_0)||p_{\theta }(x_t|x_{t+1})\right);1\le t\le t-1\\ l_0& =-\log p_{\theta }\left(x_0|x_1\right)\end{array}$$

最终是优化两个高斯分布 $q(x_t|x_{t-1},x_0)=\mathcal{n}\left(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_t\mathbf{i}\right)$ (详见公式 (7)) 与 $p_{\theta }(x_t|x_{t+1})=\mathcal{n}\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\sigma }_{\theta }\right)$ (详见公式(6), 此为模型预估的分布)之间的 kl 散度. 由于多元高斯分布的 kl 散度存在闭式解, 详见: multivariate_normal_distributions, 从而可以得到:

$$\begin{array}{rl}{l}_t& ={\mathbb{e}}_{x_0,ϵ}[\frac{1}{2\Vert {\mathbf{\sigma }}_{\theta }(x_t,t){\Vert }_2^2}\Vert {\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t){\Vert }^2]\\ & ={\mathbb{e}}_{x_0,ϵ}[\frac{1}{2\Vert {\mathbf{\sigma }}_{\theta }{\Vert }_2^2}\Vert \frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t)-\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }(x_t,t)\left){\Vert }^2\right]\\ & ={\mathbb{e}}_{x_0,ϵ}[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\sigma }}_{\theta }{\Vert }_2^2}\Vert {ϵ}_t-{ϵ}_{\theta }(x_t,t){\Vert }^2];\text{其中}{ϵ}_t\text{为高斯噪声},{ϵ}_{\theta }\text{为模型学习的噪声}\\ & ={\mathbb{e}}_{x_0,ϵ}[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\sigma }}_{\theta }{\Vert }_2^2}\Vert {ϵ}_t-{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t,t){\Vert }^2]\end{array}$$

ddpm 将 loss 简化为如下形式:

l t simple  = e x 0 , ϵ t [ ∥ ϵ t − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) ∥ 2 ] \begin{align} l_t^{\text {simple }}=\mathbb{e}_{x_0, \epsilon_t}\left[\left\|\epsilon_t-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon_t, t\right)\right\|^2\right] \end{align} ltsimple ​=ex0​,ϵt​​[ ​ϵt​−ϵθ​(αˉt​ ​x0​+1−αˉt​ ​ϵt​,t) ​2]​​

因此 diffusion 模型的目标函数即是学习高斯噪声 ${ϵ}_t$ 和 ${ϵ}_{\theta }$ (来自模型输出) 之间的 mse loss.

最终算法

最终 ddpm 的算法流程如下:

训练阶段重复如下步骤:

• 从数据集中采样 $x_0$
• 随机选取 time step $t$
• 生成高斯噪声 ${ϵ}_t\in \mathcal{n}(0,\mathbf{i})$
• 调用模型预估 ${ϵ}_{\theta }\left(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t,t\right)$
• 计算噪声之间的 mse loss: ∥ ϵ t − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) ∥ 2 \left\|\epsilon_t-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon_t, t\right)\right\|^2 ​ϵt​−ϵθ​(αˉt​ ​x0​+1−αˉt​ ​ϵt​,t) ​2, 并利用反向传播算法训练模型.

逆向阶段采用如下步骤进行采样:

• 从高斯分布采样 $x_t$
• 按照 $t,\dots ,1$ 的顺序进行迭代:
  • 如果 $t=1$, 令 $\mathbf{z}=0$; 如果 $t>1$, 从高斯分布中采样 $\mathbf{z}\sim \mathcal{n}(0,\mathbf{i})$
  • 利用公式 (12) 学习出均值 ${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))$, 并利用公式 (8) 计算均方差 ${\sigma }_t=\sqrt{{\tilde{\beta }}_t}=\sqrt{\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t}$
  • 通过重参数技巧采样 $x_{t-1}={\mu }_{\theta }(x_t,t)+{\sigma }_t\mathbf{z}$
• 经过以上过程的迭代, 最终恢复 $x_0$.

源码分析

ddpm 文章以及代码的相关信息如下:

• denoising diffusion probabilistic models 论文,
  • 其 tf 源码位于: https://github.com/hojonathanho/diffusion, 源码介绍以该版本为主
  • pytorch 的开源实现: https://github.com/lucidrains/denoising-diffusion-pytorch, 核心逻辑和上面 tensorflow 版本是一致的, stable diffusion 参考的是 pytorch 版本的代码.

本文以分析 tensorflow 源码为主, pytorch 版本的代码和 tensorflow 版本的实现逻辑大体不差的, 变量名字啥的都类似, 阅读起来不会有啥门槛. tensorlow 源码对 diffusion 模型的实现位于 diffusion_utils_2.py, 模型本身的分析以该文件为主.

训练阶段

以 cifar 数据集为例.

在 run_cifar.py 中进行前向传播计算 loss:

• 第 6 行随机选出 t ∼ uniform ( { 1 , … , t } ) t\sim\text{uniform}(\{1, \ldots, t\}) t∼uniform({1,…,t})
• 第 7 行 training_losses 定义在 gaussiandiffusion2 中, 计算噪声间的 mse loss.

进入 gaussiandiffusion2 中, 看到初始化函数中定义了诸多变量, 我在注释中使用公式的方式进行了说明:

下面进入到 training_losses 函数中:

• 第 19 行: self.model_mean_type 默认是 eps, 模型学习的是噪声, 因此 target 是第 6 行定义的 noise, 即 ${ϵ}_t$
• 第 9 行: 调用 self.q_sample 计算 $x_t$, 即公式 (3) $x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t$
• 第 21 行: denoise_fn 是定义在 unet.py 中的 unet 模型, 只需知道它的输入和输出大小相同; 结合第 9 行得到的 $x_t$, 得到模型预估的噪声: ${ϵ}_{\theta }\left(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t,t\right)$
• 第 23 行: 计算两个噪声之间的 mse: ∥ ϵ t − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) ∥ 2 \left\|\epsilon_t-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon_t, t\right)\right\|^2 ​ϵt​−ϵθ​(αˉt​ ​x0​+1−αˉt​ ​ϵt​,t) ​2, 并利用反向传播算法训练模型

上面第 9 行定义的 self.q_sample 详情如下:

• 第 13 行的 q_sample 已经介绍过, 不多说.
• 第 2 行的 _extract 在代码中经常被使用到, 看到它只需知道它是用来提取系数的即可. 引入输入是一个 batch, 里面的每个样本都会随机采样一个 time step $t$, 因此需要使用 tf.gather 来将 $\overline{{\alpha }_t}$ 之类选出来, 然后将系数 reshape 为 [b, 1, 1, ....] 的形式, 目的是为了利用 broadcasting 机制和 $x_t$ 这个 tensor 相乘.

前向的训练阶段代码实现非常简单, 下面看逆向阶段

逆向阶段

逆向阶段代码定义在 gaussiandiffusion2 中:

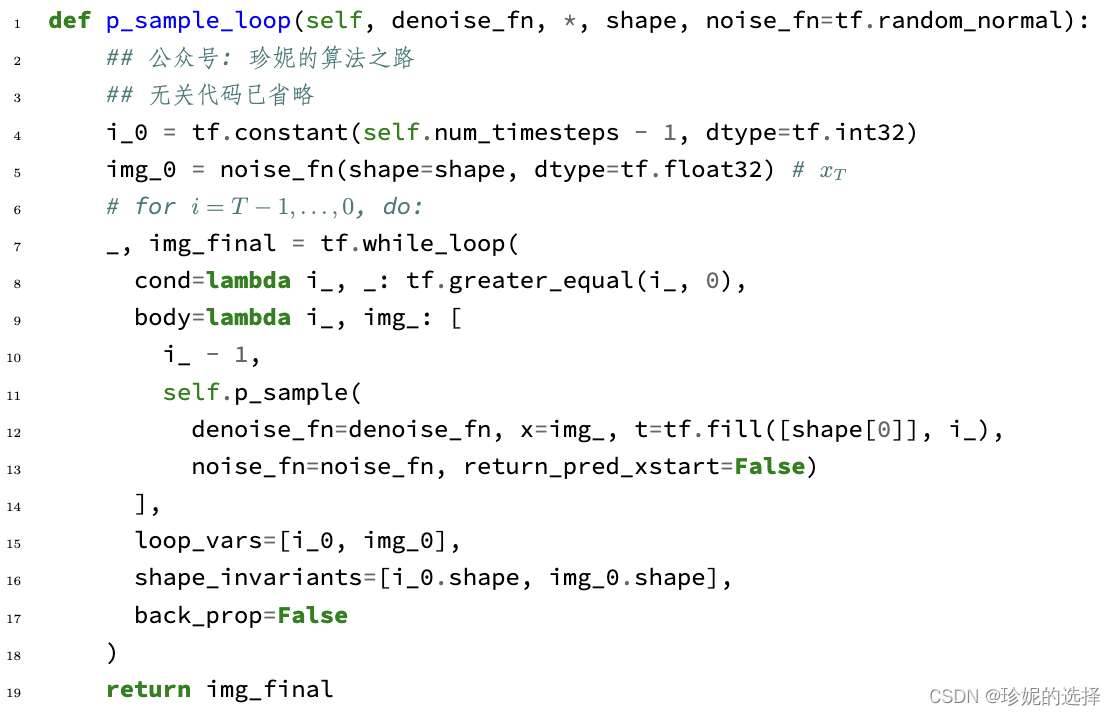
• 第 5 行生成高斯噪声 $x_t$, 然后对其不断去噪直至恢复原始图像
• 第 11 行的 self.p_sample 就是公式 (6) $p_{\theta }\left(x_{t-1}\mid x_t\right)=\mathcal{n}\left(x_{t-1};{\mu }_{\theta }\left(x_t,t\right),{\sigma }_{\theta }\left(x_t,t\right)\right)$ 的过程, 使用模型来预估 ${\mu }_{\theta }\left(x_t,t\right)$ 以及 ${\sigma }_{\theta }\left(x_t,t\right)$
• 第 12 行的 denoise_fn 在前面说过, 是定义在 unet.py 中的 unet 模型; img_ 表示 $x_t$.
• 第 13 行的 noise_fn 则默认是 tf.random_normal, 用于生成高斯噪声.

进入 p_sample 函数:

• 第 7 行调用 self.p_mean_variance 生成 ${\mu }_{\theta }\left(x_t,t\right)$ 以及 $\log \left({\sigma }_{\theta }\left(x_t,t\right)\right)$, 其中 ${\sigma }_{\theta }\left(x_t,t\right)$ 通过计算 ${\tilde{\beta }}_t$ 得到.
• 第 11 行从高斯分布中采样 $\mathbf{z}$
• 第 18 行通过重参数技巧采样 $x_{t-1}={\mu }_{\theta }(x_t,t)+{\sigma }_t\mathbf{z}$, 其中 ${\sigma }_t=\sqrt{{\tilde{\beta }}_t}$

进入 self.p_mean_variance 函数:

• 第 6 行调用模型 denoise_fn, 通过输入 $x_t$, 输出得到噪声 ${ϵ}_t$
• 第 19 行 self.model_var_type 默认为 fixedlarge, 但我当时看 fixedsmall 比较爽, 因此 model_variance 和 model_log_variance 分别为 ${\tilde{\beta }}_t=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$ (见公式 8), 以及 $\log {\tilde{\beta }}_t$
• 第 29 行调用 self._predict_xstart_from_eps 函数, 利用公式 (10) 得到 $x_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)$
• 第 30 行调用 self.q_posterior_mean_variance 通过公式 (9) 得到 ${\mu }_{\theta }(x_t,x_0)=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0$

self._predict_xstart_from_eps 函数相亲如下:

• 该函数计算 $x_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)$

self.q_posterior_mean_variance 函数详情如下:

• 相关说明见注释, 另外发现对于 ${\mu }_{\theta }(x_t,x_0)$ 的计算使用的是公式 (9) ${\mu }_{\theta }(x_t,x_0)=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0$ 而不是进一步推导后的公式 (11) ${\mu }_{\theta }(x_t,x_0)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t)$.

总结

写文章真的挺累的, 好处是, 我发现写之前我以为理解了, 但写的过程中又发现有些地方理解的不对. 写完后才终于把逻辑理顺.