我要评论正态分布检验
雅克-贝拉检验（jarque-bera-test）（jb检验）
介绍
jb检验主要适用于样本数量大于30，而且样本数越多，jb检验效果越准确。
jb检验主要用于判断数据是否符合总体正态分布，而且构造的jb统计量需要符合自由度为2的卡方分布，即为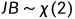
。jb统计量如下所示。
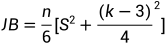（n为样本量，s为偏度，k为峰度）
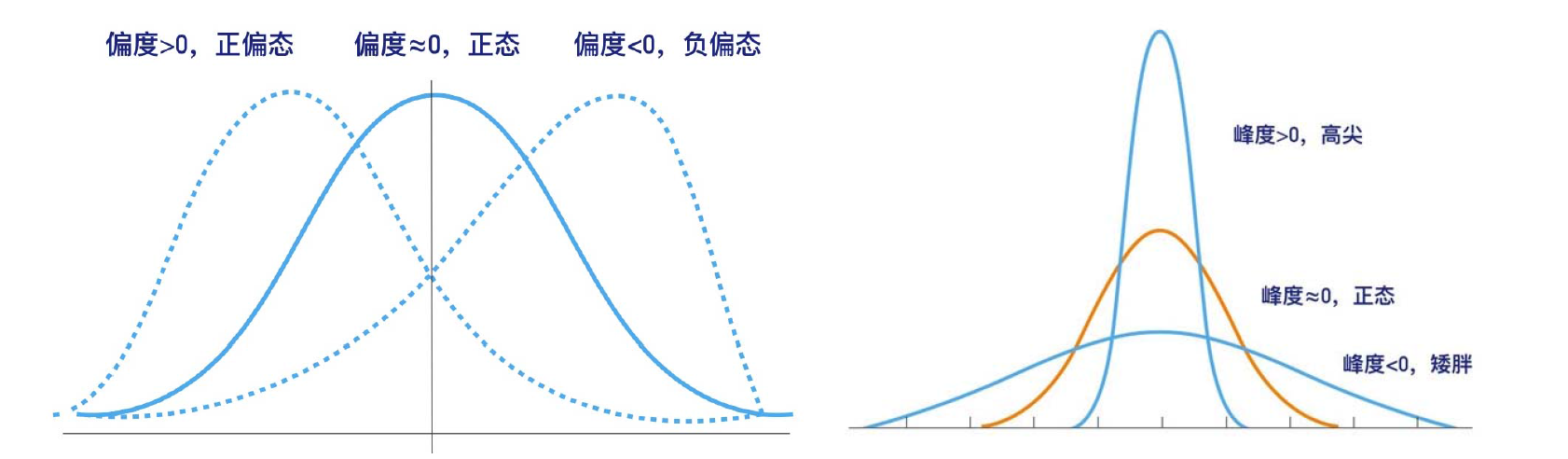
jb检验主要利用峰度和偏度构造jb统计量，峰度和偏度的直观表现形式如图所示。峰度越大，体现即为曲线越陡峭，峰度越低，曲线约平缓。偏度约大，远离标准正态分布，偏度越小，也是远离标准正态分布。如图所示。
步骤
1. 构造假设h0和h1，分别为
h0：该随机变量服从正态分布。
h1：该随机变量不服从正态分布。
2. 求出数据的峰度和偏度，构造jb统计量，确定相对应置信水平下的拒绝域和接受域。计算得出p值，如果p值大于0.05，我们不能拒绝原假设（h0），否则我们可以拒绝原假设。
具体代码
调用scipy实现
def jb_test(data):
# 样本规模数量n
n = data.size
data_distance = data - data.mean()
'''
m2:二阶中心距
skew为偏度, skew = 三阶中心距跟m2^1.5的比
krut为峰度， krut = 四节中心距与m2^2的比
'''
skew = stats.skew(y)
krut = stats.kurtosis(y) + 3
'''
计算jb检验量，而且建立假设检验
'''
# 公式
jb = n * (skew**2 / 6 + (krut - 3)**2 / 24)
# 双侧检验
p_value = 1 - stats.chi2.cdf(jb, df=2)
return np.array([jb, p_value])复现构造统计量和计算p值实现
def jb_test(data):
# 样本规模数量n
n = data.size
data_distance = data - data.mean()
'''
m2:二阶中心距
skew为偏度, skew = 三阶中心距跟m2^1.5的比
krut为峰度， krut = 四节中心距与m2^2的比
'''
m2 = np.mean(**2)
skew = np.mean(data_distance**3) / m2**1.5
krut = np.mean(data_distance**4) / m2**2
'''
计算jb检验量，而且建立假设检验
'''
# 公式
jb = n * (skew**2 / 6 + (krut - 3)**2 / 24)
# 双侧检验
p_value = 1 - stats.chi2.cdf(jb, df=2)
return np.array([jb, p_value])夏皮洛-威尔克检验（shapiro-wilk）检验
介绍
shapiro-wilk检验又称为w检验，适用于一定样本量n（8<n<50）的研究对象总是符合正态分布。将样本量为n的样本按照大小顺序编排，然后根据公式计算统计量w的值，该值越接近于1，且显著水平大于0.05时，我们就没法拒绝原假设。
w统计量构造如下，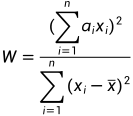
代码
def shapiro_wilk_test(data):
# 利用shapiro-wilk test检验其是否服从正态分布
return stats.shapiro(data)
# 输出（统计量w的值,p值）
# w的值越接近1就越表明数据和正态分布拟合得越好，p值>指定水平,不拒绝原假设，可以认为样本数据服从正态分布
发表评论