论文阅读笔记 三遍阅读详解知识图谱入门之作(A Survey on Knowledge Graphs)_知识图谱survey(2)

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上软件测试知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

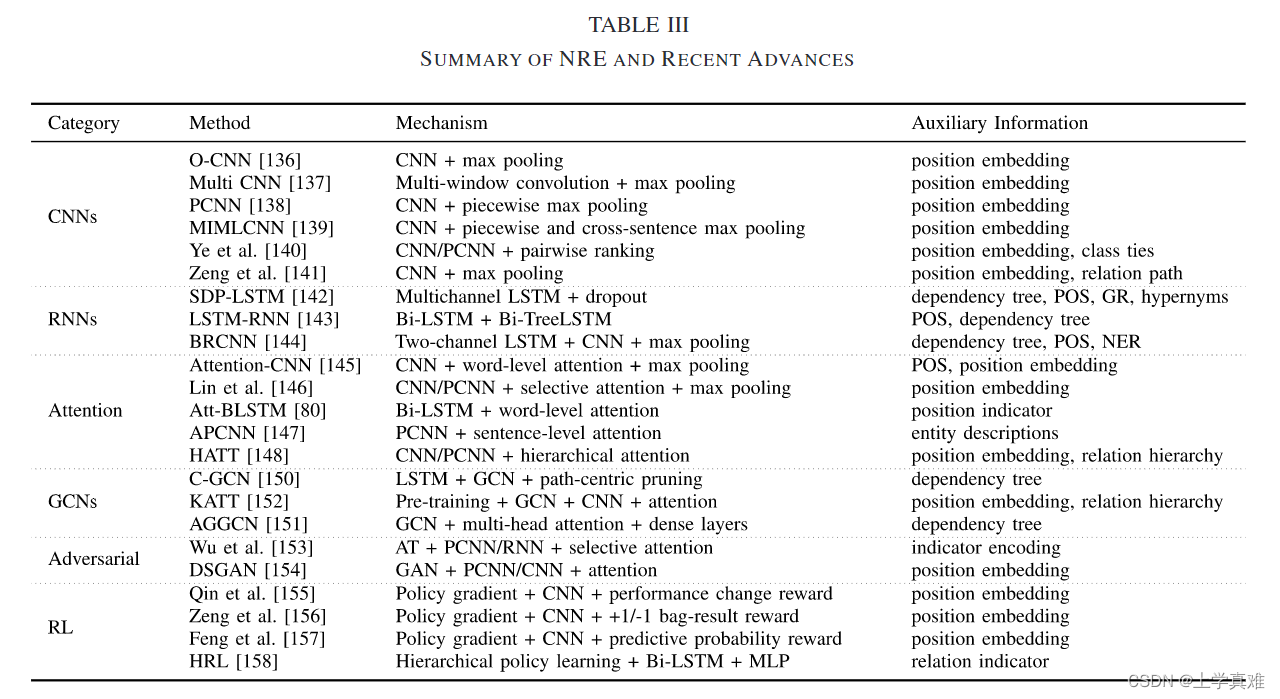
第三个表是比较神经网络提取关系的模型，给出了各个模型从属的类别，机制以及对应的辅助信息。

到这里，我们的泛读也就结束了，泛读完成我们可以回答这三个问题了

1. 论文要解决什么问题？

论文建立在知识图谱模型复杂多样的背景下，提出了一个综合性的survey。
2. 论文采用了什么方法？

论文提出了新的分类标准，对各个模型进行分类。
3. 论文达到什么效果？

由于是survey，所以没有实验部分。

精读论文

introduction

第一段主要介绍了知识图谱已经吸引了学术界和工业界的注意力，并且对于知识图谱的各个部分的组成进行了介绍，包含实体，关系，语义描述等。原文是这么说的

第二段讲了知识图谱和知识库的关系，然后通过一个实例描述了知识图谱是由三元组构成的。

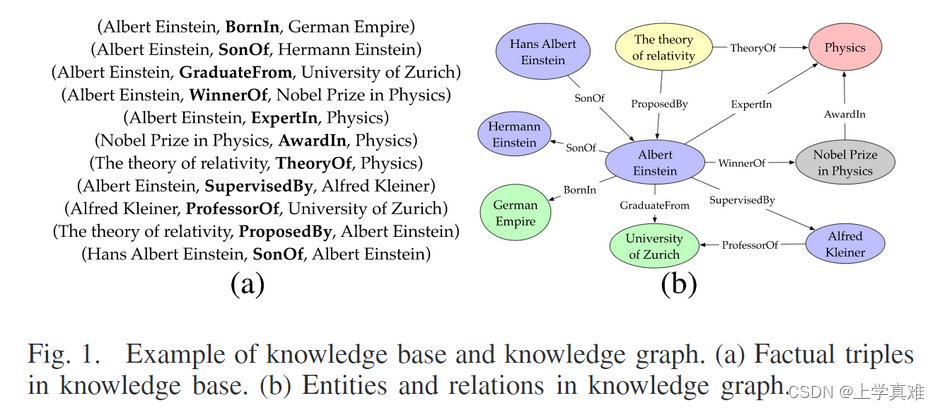
也就是上面这个图片中的内容

第三段介绍了最近的发展，同时引出作者的分类，krl或者叫kge是映射实体到低维的向量。介绍了知识获取任务包含kgc，三元组分类，实体识别，关系抽取。受益于多种信息的发展，然后讲了现实中的应用。

第四段开始总结，并说明创新点，主要包含以下四点：

1. comprehensive review，综合的视角
2. full-view categorization and new taxonomies: 全视角的分类，作者又说了一下怎么分类的。
3. wide coverage on emerging advances: 对于热点事件的讨论
4. summary and outlook on future directions: 总结和讨论未来方向

在最后作者说了一下本文的结构。

overview

brief history of knowledge bases

这里介绍知识图谱的历史。从1956年提出语义网概念开始，一直到rdf，owl和语义网的出现，接下来许多开放的知识库相继发布，例如wordnet、dbpedia、yago和freebase。再到2012年知识图谱的应用。

definitions and notations

作者这里说关于知识图谱还没有一个广泛认可的正式定义，列举了两篇的定义。

将知识图谱定义成

g

=

{

e

,

r

,

f

}

\mathcal{g} = {{\mathcal{e}, \mathcal{r}, \mathcal{f}}}

g={e,r,f}

其中

e

,

r

,

f

\mathcal{e}, \mathcal{r}, \mathcal{f}

e,r,f分别表示实体、关系和事实的集合。一个事实定义成三元组

(

h

,

r

,

t

)

∈

f

(h, r, t)\in \mathcal{f}

(h,r,t)∈f

categorization of research on knowledge graph

这里的分类就是这一张图

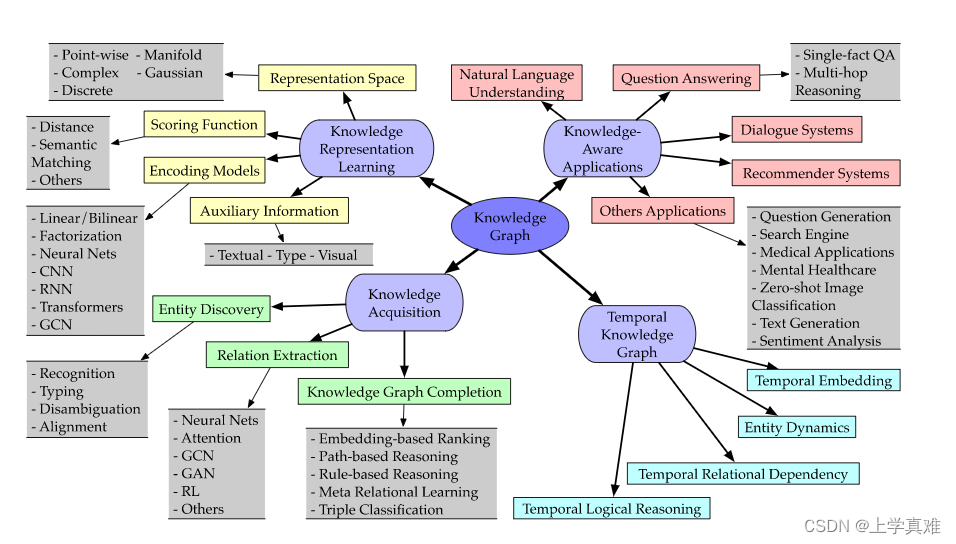
分为krl，knowledge acquisition，knowledge aware application和temporal knowledge graph。

然后每个大问题又分为了几个小的课题。

related surveys

相关的综述，作者主要提到的主要相关的有两篇，并且指出，这些综述的描述视角太单一了。

knowledge representation learning

知识表示学习(krl)也可称为知识嵌入学习(kge)，多关系学习和统计关系学习（srl），这一节主要讲了四个角度进行的表示学习方法。

注：本文涉及的模型较多，每个小节我都会以一个模型为例，解释论文中想表达的意思。通过一篇综述是无法理解这么多模型的，因此简单的重复列出也无意义，具体的其他模型可以看原文。

representation space

首先是表示空间，作者在这里指出，表示学习的关键就是学习得到实体和关系的低维嵌入，在我理解也就是如何把知识在低维的空间内表示出来。

主要从四个空间进行描述，并通过相应的模型来说明。

• pointwise space:

点对点的空间，其实主要是欧式空间，嵌入的形式是将实体和关系映射到向量或矩阵空间，或者更高维，用来捕获关系的交互信息。如图a，可以用一维的vector，二维的matrix，三维的tensor以至于更高纬度。

以一个例子为例，剩下的也都是简述，要看懂，可能得看具体的论文。

transe在d dd维的向量空间中表示实体和关系，例如

h

,

t

,

r

∈

r

d

\mathbf{h}, \mathbf{t}, \mathbf{r} \in \mathbb{r}^d

h,t,r∈rd，使得嵌入服从如下的转换规则：

h

r

≈

t

\mathbf{h} + \mathbf{r} \approx \mathbf{t}

h+r≈t。

• complex vector space

与实值空间不同，这里是将实体和关系投影到复向量空间，其中

h

,

t

,

r

∈

c

d

\mathbf{h}, \mathbf{t}, \mathbf{r} \in \mathbb{c}^d

h,t,r∈cd。以

h

\mathbf{h}

h为例，它有实值部分

r

e

(

h

)

re(\mathbf{h})

re(h)也有虚值部分

i

m

(

h

)

im(\mathbf{h})

im(h)，

h

=

r

e

(

h

)

i

i

m

(

h

)

\mathbf{h}=re(\mathbf{h})+iim(\mathbf{h})

h=re(h)+iim(h)。如图b所示。

complex首先引入了图 3b所示的复杂向量空间，可以捕获到对称的和反对称的关系。使用hermitian点乘来结合头实体和关系，以及尾实体的共轭。

• gaussian distribution

高斯分布是通过一个分布关系来表达实体和关系的。如图c。

基于密度的嵌入模型kg2e引入了高斯分布来处理确定的/不确定的实体和关系。作者将实体和关系嵌入到了一个多维度的高斯分布

h

∼

n

(

μ

h

,

∑

h

)

\mathcal{h}\sim \mathcal{n}(\mu_h, \sum_h)

h∼n(μh​,∑h​)和

t

∼

n

(

μ

h

,

∑

h

)

\mathcal{t}\sim \mathcal{n}(\mu_h, \sum_h)

t∼n(μh​,∑h​)中。均值向量

μ

\mu

μ表示了实体和关系的位置，协方差矩阵

∑

\sum

∑建模了它们的确定性/不确定性。根据转换（translational）的规则，实体转换的概率分布

h

−

t

\mathcal{h}-\mathcal{t}

h−t定义为

p

e

∼

n

(

μ

h

−

μ

t

,

∑

h

∑

t

)

\mathcal{p}_e \sim \mathcal{n}(\mu_h-\mu_t, \sum_h+\sum_t)

pe​∼n(μh​−μt​,∑h​+∑t​)。

• manifold and group

这里是知识在流形空间和群的表示，manifold（流行）是一个拓扑空间，可以定义成具有领域的点的集合。group（群）是抽象代数中定义的内容。作者提到，pointwise中的嵌入，打分函数远超过实体和关系的数量。

mainfolde将point-wise嵌入扩展成mainfold-based嵌入。作者引入了两种mainfold-based嵌入的设置，sphere（球体）和hyperplane（超平面）。例如图 3d所示，对于球体的设置，再生希尔伯特核空间（reproducing kernel hilbert space）用于表示mainfold函数。另一个超平面的设置的引入通过交叉嵌入（intersected embeddings）增强了模型。

scoring function

打分函数被用于衡量事实的合理性，也在基于能量的学习框架中被称作能量函数。基于能量的学习旨在学习到能量函数

e

θ

(

x

)

\mathcal{e}_{\theta}(x)

eθ​(x)使得正样本得分高于负样本。事实上，关系的表示通常反映在打分函数里。

文中将打分函数分为两类，基于距离的和基于相似性的用来衡量事实的合理性，分别如图a和图b所示：

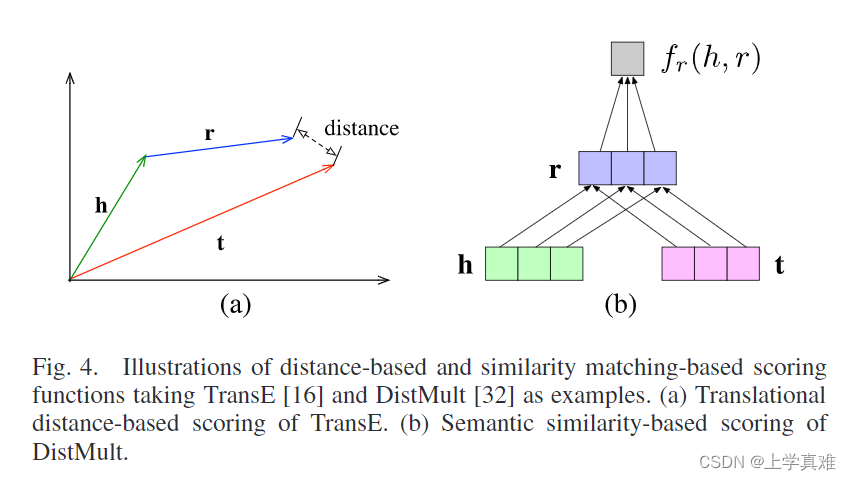
基于距离的打分函数通过计算实体之间的距离来衡量合理性，如经典模型transe通过计算头实体和关系是否与尾实体在向量空间相近来打分。

基于语义相似度的打分通过语义匹配来衡量合理性，如经典模型distmult的

h

t

m

r

≈

t

t

\mathbf{h}^t\mathbf{m}_r \approx \mathbf{t}^t

htmr​≈tt，在表示空间将头实体转化到尾实体的相近的地方。

作者下面主要列出了这两种方法，并举了很多模型的例子，我这里还是挑一个模型来说，理解其意思即可。

• distance-based scoring funtion

意思是基于距离的打分函数，一个直觉的方法是计算实体的关系投影之间的欧式距离，如se模型使用两个投影矩阵和

l

1

l_1

l1​距离来学习结构的嵌入，公式如下所示：

f

r

(

h

,

t

)

=

∥

m

r

,

1

h

−

m

r

,

2

t

∥

l

1

.

f_r(h,t)= \vert m_{r,1}h-m_{r,2}t \vert_{l_1}.

fr​(h,t)=∥mr,1​h−mr,2​t∥l1​​.

从我目前的理解来看，这公式的意思就是将头实体h在关系上的投影和尾实体t在关系上的投影的距离差，通过这个差来衡量学习到的事实是否合理。

这里更广泛使用的是转换的打分函数，它将关系看成是从头实体到尾实体的“翻译”来学习嵌入。如transe方法就是假定

h

r

\mathbf{h} + \mathbf{r}

h+r的嵌入应该和

t

\mathbf{t}

t的嵌入接近，然后在l1或l2的约束下定义了打分函数，如下公式所示：

f

r

(

h

,

t

)

=

∥

h

r

−

t

∥

l

1

/

l

2

f_r(h,t)=\vert \mathbf{h+r-t} \vert_{l_1/l_2}

fr​(h,t)=∥h+r−t∥l1​/l2​​

• semantic matching

这里是另一种方法来衡量合理性，即计算语义相似性，一般是通过乘法来实现。

distmult考虑最基本的双线性打分函数：

g

r

b

(

y

e

1

,

y

e

2

)

=

y

e

1

t

m

r

y

e

2

g^{b_r(y_{e_1},y_{e_2})=y}t_{e_1}m_ry_{e_2}

grb​(ye1​​,ye2​​)=ye1​t​mr​ye2​​

将这个双线性打分函数限制到对角线，减少参数量，如下所示：

f

r

(

h

,

t

)

=

h

⊤

d

i

a

g

(

m

r

)

t

f_r(h,t)=\mathbf{h}^\top diag(\mathbf{m}_r)\mathbf{t}

fr​(h,t)=h⊤diag(mr​)t

encoding models

这里是介绍用特定的模型结构，对实体间的交互信息以及关系进行编码的模型，包括以下三种

1. 线性/双线性模型(linear/bilinear models)，通过将表示空间的头实体投影到尾实体相近的位置，将关系化为了线性/双线性的映射。
2. 分解模型(factorization models)，旨在将关系数据分解为低秩的矩阵，以用于表示学习。
3. 神经网络(neural networks)，使用非线性激活函数编码关系数据并通过网络结构匹配实体和关系的语义相似性。

一些神经网络模型如下图所示：

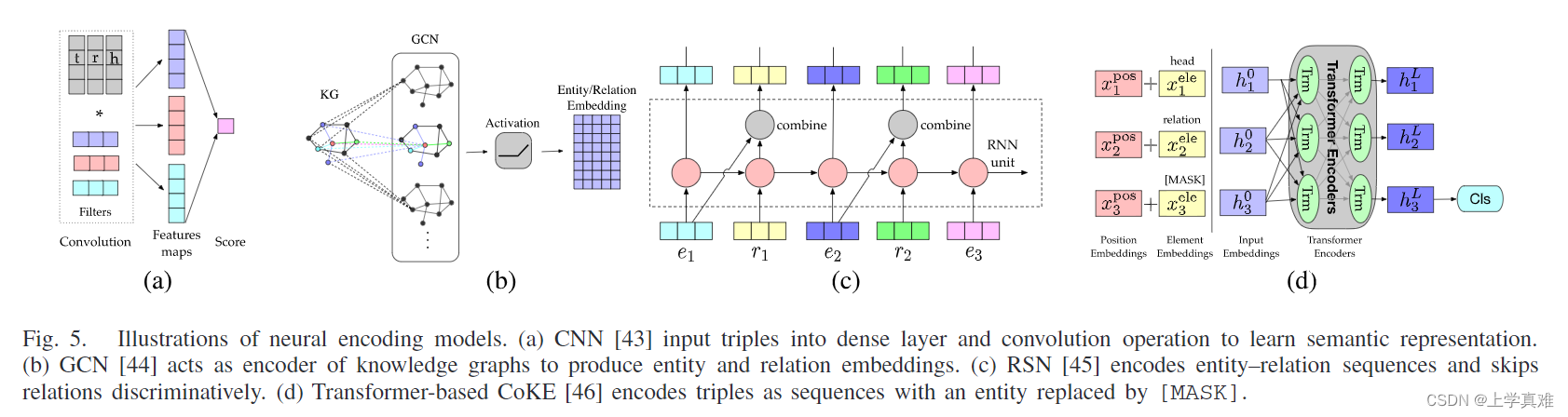
• linear/bilinear models

线性/非线性模型使用线性操作对实体交互和关系进行编码，下式是线性的转换操作：

g

r

(

h

,

t

)

=

m

r

t

(

h

t

)

g_r(\mathbf{h,t})=\mathbf{m_r^t}\binom{\mathbf{h}}{\mathbf{t}}

gr​(h,t)=mrt​(th​)

双线性的转换上面其实已经给出了，这里再给一遍：

g

r

b

(

y

e

1

,

y

e

2

)

=

y

e

1

t

m

r

y

e

2

g^{b_r(y_{e_1},y_{e_2})=y}t_{e_1}m_ry_{e_2}

grb​(ye1​​,ye2​​)=ye1​t​mr​ye2​​

使用线性/双线性的方法括se, sme, distmult, complex, analogy。

使用l2正则化的transe，打分函数可以扩展成对一维向量的线性转换：

∥

h

r

−

t

∥

2

2

=

2

r

t

(

h

−

t

)

−

2

h

t

t

∥

r

∥

2

2

∥

h

∥

2

2

∥

t

∥

2

2

\vert \mathbf{h+r-t} \vert_2^2 = 2\mathbf{r}^{t\mathbf{(h-t)}-2\mathbf{h}}t\mathbf{t}+\vert \mathbf{r} \vert_2^2 +\vert \mathbf{h} \vert_2^2 +\vert \mathbf{t} \vert_2^2

∥h+r−t∥22​=2rt(h−t)−2htt+∥r∥22​+∥h∥22​+∥t∥22​

• factorization models

分解模型将krl问题建模成了三个张量的分解。

张量分解的规则可以定义成：

x

h

r

t

≈

h

t

m

r

t

\mathcal{x}_{hrt} \approx \mathbf{h}^t \mathbf{m}_r \mathbf{t}

xhrt​≈htmr​t，分解函数遵循语义匹配的模式。双线性模型的开山之作是rescal，是发表icml 2011上的工作。主要思想是三维张量分解。在知识图谱张量的关系片(slice)上进行分解，关系片是一个矩阵，每个矩阵类似图的邻接矩阵。对tenor分解为以下的公式：

χ

k

=

a

r

k

a

t

\chi_k = \mathbf{ar_ka}^t

χk​=ark​at

a

a

a是 n×r 的矩阵，表示每个实体的隐性表示（latent-component representation），

r

k

r_k

rk​是 r×r 的非对称矩阵，建模第 k 个属性/关系中的实体 latent component 的交互。

• neural networks

神经网络在语义匹配上效果出色，使用线性和双线性的模型也可以使用神经网络。而用于表示学习的神经模型包括多层感知机（mlp）、神经张量网络（ntn）和神经关联模型（nam）。一般来说，这些方法将实体和关系输入到深层神经网络中，并计算语义匹配分数。mlp使用全连接层编码实体和关系，并使用带有非线性激活函数的第二层对三元组进行打分：

f

r

(

h

,

t

)

=

σ

(

w

⊤

σ

(

w

[

h

,

r

,

t

]

)

)

f_r(h,t)=\sigma(\mathbf{w}^\top\sigma(\mathbf{w[h,r,t]}))

fr​(h,t)=σ(w⊤σ(w[h,r,t]))

其中

w

∈

r

n

×

3

d

\mathbf{w}\in \mathbb{r}^{n\times 3d}

w∈rn×3d是权重矩阵，

[

h

,

r

,

t

]

\mathbf{[h,r,t]}

[h,r,t]是三个向量的拼接。

• convolutional neural networks

cnn被用来学习深层的表示特征，如conve

嵌入上使用2d的卷积，并使用多层的非线性特征，通过将头实体和关系映射成2d的矩阵，来建模实体间和关系间的交互。例如

m

h

∈

r

d

w

×

d

h

\mathbf{m}_h \in \mathbb{r}^{d_w\times d_h}

mh​∈rdw​×dh​和

m

r

∈

r

d

w

×

d

h

\mathbf{m}_r \in \mathbb{r}^{d_w\times d_h}

mr​∈rdw​×dh​。打分函数定义为：

f

r

(

h

,

t

)

=

σ

(

v

e

c

(

σ

(

[

m

h

;

m

r

]

∗

ω

)

)

w

)

t

f_r(h,t)=\sigma(vec(\sigma(\mathbf{[m_h;m_r]*\omega}))\mathbf{w})\mathbf{t}

fr​(h,t)=σ(vec(σ([mh​;mr​]∗ω))w)t

其中

ω

\mathbf{\omega}

ω是卷积核，

v

e

c

vec

vec是将tensor reshape成向量的向量化操作。

通过堆叠多层并进行非线性的特征学习，conve可以学习到语义级别的信息。

• recurrent neural networks

为了捕获到kg中更长的关系依赖，可以使用基于rnn的方法。

如本节最开始的d图所示的rsn，设计了循环skip机制，通过区分实体和关系，来增强语义表示学习。

包含实体和关系的关系路径例如

(

x

1

,

x

2

,

.

.

.

,

x

t

)

(x_1, x_2, …, x_t)

(x1​,x2​,…,xt​)，是随机游走产生的，并且元素的位置和互换。然后使用其来计算循环隐层状态

h

t

=

t

a

n

h

(

w

h

h

t

−

1

w

x

x

t

b

)

\mathbf{h}_t = tanh(\mathbf{w}h \mathbf{h}{t-1} + \mathbf{w}_x \mathbf{x}_t + b)

ht​=tanh(whht−1+wx​xt​+b)。skip操作如下，其中

s

1

\mathbf{s}_1

s1​，

s

2

\mathbf{s}_2

s2​是权重矩阵。

h

t

′

=

{

h

t

x

t

∈

ε

s

1

h

t

s

2

x

t

−

1

x

t

∈

r

\mathbf{h_t}'=\left{ \begin{array}{lr}\mathbf{h_t}&x_t\in \mathcal{\varepsilon}\ \mathbf{s_1h_t+s_2x_{t-1}}&x_t\in\mathcal{r} \end{array} \right.

ht​′={ht​s1​ht​+s2​xt−1​​xt​∈εxt​∈r​

• transformers

基于transformer的模型促进了利用上下文本文的表示学习。

为了利用kg中的上下文信息，coke使用transformers来建模边和路径的序列。类似地，kg-bert借鉴了语言模型的预训练思想并使用transformer中的双向编码表示作为编码实体和关系的encoder。

• graph neural networks

图神经网络（gnn）是使用encoder-decoder框架学习结构的连通性。

r-gcn提出了针对关系的转换来建模有向的kg，模型的前向传播定义成：

x

i

(

l

1

)

=

σ

(

∑

r

∈

r

∑

j

∈

n

i

r

1

c

i

,

r

w

r

(

l

)

x

j

(

l

)

w

0

(

l

)

x

i

(

l

)

)

.

x_i^{(l+1)}=\sigma\left(\sum_{r\in\mathcal{r}} \sum_{j\in n_i^r} \frac{1}{c_{i,r}}w_r^{(l)} x_j^{(l)}+w_0{(l)}x_i^{(l)}\right).

xi(l+1)​=σ⎝⎛​r∈r∑​j∈nir​∑​ci,r​1​wr(l)​xj(l)​+w0(l)​xi(l)​⎠⎞​.

其中

x

i

(

l

)

∈

r

d

(

l

)

x^{(l)}_i\in \mathbb{r}^{d{(l)}}

xi(l)​∈rd(l)是第l层第i个实体的隐层状态；

n

i

r

n^r_i

nir​是和第i个实体有关系

r

∈

r

r\in r

r∈r 的邻居；

w

0

(

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上软件测试知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

s2​是权重矩阵。

h

t

′

=

{

h

t

x

t

∈

ε

s

1

h

t

s

2

x

t

−

1

x

t

∈

r

\mathbf{h_t}'=\left{ \begin{array}{lr}\mathbf{h_t}&x_t\in \mathcal{\varepsilon}\ \mathbf{s_1h_t+s_2x_{t-1}}&x_t\in\mathcal{r} \end{array} \right.

ht​′={ht​s1​ht​+s2​xt−1​​xt​∈εxt​∈r​

• transformers

基于transformer的模型促进了利用上下文本文的表示学习。

为了利用kg中的上下文信息，coke使用transformers来建模边和路径的序列。类似地，kg-bert借鉴了语言模型的预训练思想并使用transformer中的双向编码表示作为编码实体和关系的encoder。

• graph neural networks

图神经网络（gnn）是使用encoder-decoder框架学习结构的连通性。

r-gcn提出了针对关系的转换来建模有向的kg，模型的前向传播定义成：

x

i

(

l

1

)

=

σ

(

∑

r

∈

r

∑

j

∈

n

i

r

1

c

i

,

r

w

r

(

l

)

x

j

(

l

)

w

0

(

l

)

x

i

(

l

)

)

.

x_i^{(l+1)}=\sigma\left(\sum_{r\in\mathcal{r}} \sum_{j\in n_i^r} \frac{1}{c_{i,r}}w_r^{(l)} x_j^{(l)}+w_0{(l)}x_i^{(l)}\right).

xi(l+1)​=σ⎝⎛​r∈r∑​j∈nir​∑​ci,r​1​wr(l)​xj(l)​+w0(l)​xi(l)​⎠⎞​.

其中

x

i

(

l

)

∈

r

d

(

l

)

x^{(l)}_i\in \mathbb{r}^{d{(l)}}

xi(l)​∈rd(l)是第l层第i个实体的隐层状态；

n

i

r

n^r_i

nir​是和第i个实体有关系

r

∈

r

r\in r

r∈r 的邻居；

w

0

(

[外链图片转存中…(img-ihei3v63-1715540812583)]
[外链图片转存中…(img-zess4e8x-1715540812584)]
[外链图片转存中…(img-sg0vna1a-1715540812584)]

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上软件测试知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新