引言
传统方法:
- 基于翻译的方法:如transe、transd、transh、transr等
- 使用外部信息,如:
- 实体类型
- 文本描述
- 逻辑规则
这些传统方法的缺点是:忽视了概念与实例之间的区别,这导致了以下问题:
- 概念表示不足:大多数方法将概念和实例都编码为向量,这无法明确表示概念和实例之间的差异
- 对于
isa关系的敏感性不足:instanceof和subclassof(通常称为isa)是知识图谱中的两种特殊关系。
动机
层次概念:人们心中的概念是按层次组织的。因此,实例应该靠近它们所属的概念。
在transc中,概念被编码为一个球体,实例作为向量在同一语义空间中,采用相对位置来模拟概念和实例之间的关系。
符号与概念
-
关系集合 r = { r e , r c } ∪ r l \mathcal{r}=\{r_e,r_c\}\cup\mathcal{r}_l r={re,rc}∪rl,其中 r l r_{l} rl是实例之间的关系, r e r_e re是
instanceof关系, r c r_c rc是subclassof关系。 -
instanceof三元组集合 s e = { ( i , r e , c ) k } k = 1 n e , \mathcal{s_{e}} =\{(i,r_{e} ,c)_{k}\}^{n_{e}}_{k=1}, se={(i,re,c)k}k=1ne,
其中 i ∈ i , c ∈ c , n e i \in \mathcal{i}, c \in c, n_{e} i∈i,c∈c,ne是 s e s_{e} se的大小 -
subclassof三元组集合 s c = { ( c i , r c , c j ) k } k = 1 n c , \mathcal{s_{c}}=\{(c_{i},r_{c},c_{j})_{k}\}^{n_{c}}_{k=1}, sc={(ci,rc,cj)k}k=1nc,
-
关系三元组: s l = { h , r , t } k = 1 n l \mathcal{s_{l}}=\{h,r,t\}_{k=1}^{n_{l}} sl={h,r,t}k=1nl
其中 h , t ∈ i h,t \in \mathcal{i} h,t∈i, r ∈ r l r \in \mathcal{r_{l}} r∈rl。 -
概念:对于 c ∈ c c \in \mathcal{c} c∈c,我们学习一个球体 s ( p , m ) s(\mathbf{p},m) s(p,m),其中 p \mathbf{p} p是球心, m m m表示半径。
-
传递性:
instanceof-subclassof的传递性关系可以表示为下列等式 ( i , r e , c 1 ) ∈ s e ∧ ( c 1 , r c , c 2 ) ∈ s c → ( i , r e , r 2 ) ∈ s e (i,r_{e},c_{1})\in s_{e} \wedge (c_{1},r_{c},c_{2})\in s_{c} \rightarrow (i,r_{e},r_{2})\in s_{e} (i,re,c1)∈se∧(c1,rc,c2)∈sc→(i,re,r2)∈sesubclassof-subclassof的传递性可以表示为: ( c 1 , r c , c 2 ) ∈ s c ∧ ( c 2 , r c , c 3 ) ∈ s c → ( c 1 , r c , c 3 ) ∈ s c (c_{1},r_{c},c_{2})\in s_{c} \wedge (c_{2},r_{c},c_{3})\in s_{c}\to (c_{1},r_{c},c_{3})\in s_{c} (c1,rc,c2)∈sc∧(c2,rc,c3)∈sc→(c1,rc,c3)∈sc
方法

作者提出了新的损失函数来衡量嵌入空间中的相对位置,并基于翻译模型共同表示概念、实例和关系。
- instanceof三元组表示:对于
instanceof三元组 ( i , r e , s ) (i,r_e,s) (i,re,s),如果为真,则 i \mathbf{i} i应该在球体 s s s内部,以表示它们之间的instanceof关系。因此,损失函数定义为 f e ( i , c ) = ∥ i − p ∥ 2 − m f_{e}(i,c)=\vert \mathbf{i}-\mathbf{p}\vert_{2}-m fe(i,c)=∥i−p∥2−m - subclassof三元组表示:对于三元组 ( c i , r c , c j ) (c_{i},r_{c},c_{j}) (ci,rc,cj),概念 c i , c j c_{i},c_{j} ci,cj被编码
为球体 s i ( p i , m i ) s_{i}(p_{i},m_{i}) si(pi,mi)。如果 c i c_i ci是 c j c_{j} cj的子类,则它们的中心应该接近。但是,球体 s i s_{i} si和 s j s_{j} sj之间存在许多相对位置。因此,损失函数定义为 d = ∥ p i − p j ∥ 2 ( a ) f c ( c i , c j ) = ∣ ∣ p i − p j ∣ ∣ 2 + m i − m j ( b ) f c ( c i , c j ) = ∣ ∣ p i − p j ∣ ∣ 2 + m i − m j ( c ) f c ( c i , c j ) = m i − m j ( d ) \begin{align} &d=\vert p_{i}-p_{j}\vert_{2} & (a)\\ & f_c(c_i,c_j)=||\mathbf{p}_i-\mathbf{p}_j||_2+m_i-m_{j} &\qquad(b) \\ & f_c(c_i,c_j)=||\mathbf{p}_i-\mathbf{p}_j||_2+m_i-m_{j} &\qquad(c) \\ &f_c(c_i,c_j)=m_i-m_{j} &(d) \end{align} d=∥pi−pj∥2fc(ci,cj)=∣∣pi−pj∣∣2+mi−mjfc(ci,cj)=∣∣pi−pj∣∣2+mi−mjfc(ci,cj)=mi−mj(a)(b)(c)(d)
- 关系三元组表示:对于 ( h , r , t ) (h,r,t) (h,r,t),损失函数如transe,定义为 f r ( h , t ) = ∥ h + r − t ∥ 2 2 f_{r}(h,t)=\vert h+r-t\vert_{2}^{2} fr(h,t)=∥h+r−t∥22
训练方法
instanceof三元组
作者使用
- ξ \xi ξ和 ξ ′ \xi' ξ′表示正例和负例三元组。
- s e \mathcal{s_{e}} se和 s e ′ \mathcal{s_{e}'} se′表示正例和负例三元组集合
- [ x ] + [x]_{+} [x]+表示 m a x ( 0 , x ) max(0,x) max(0,x)
-
γ
e
\gamma_{e}
γe是正例和负例三元组之间的间隔
l e = ∑ ξ ∈ s e ∑ ξ ′ ∈ s e ′ [ γ e + f e ( ξ ) − f e ( ξ ′ ) ] + , \mathcal{l}_e=\sum_{\xi\in\mathcal{s}_e}\sum_{\xi^{\prime}\in\mathcal{s}_e^{\prime}}[\gamma_e+f_e(\xi)-f_e(\xi^{\prime})]_+, le=ξ∈se∑ξ′∈se′∑[γe+fe(ξ)−fe(ξ′)]+,
subclassof三元组
l c = ∑ ξ ∈ s c ∑ ξ ′ ∈ s c ′ [ γ c + f c ( ξ ) − f c ( ξ ′ ) ] + , \mathcal{l}_c=\sum_{\xi\in\mathcal{s}_c}\sum_{\xi^{\prime}\in\mathcal{s}_c^{\prime}}[\gamma_c+f_c(\xi)-f_c(\xi^{\prime})]_+, lc=ξ∈sc∑ξ′∈sc′∑[γc+fc(ξ)−fc(ξ′)]+,
关系三元组
l l = ∑ ξ ∈ s l ∑ ξ ′ ∈ s l ′ [ γ l + f r ( ξ ) − f r ( ξ ′ ) ] + . \mathcal{l}_l=\sum_{\xi\in\mathcal{s}_l}\sum_{\xi^{\prime}\in\mathcal{s}_l^{\prime}}[\gamma_l+f_r(\xi)-f_r(\xi^{\prime})]_+. ll=ξ∈sl∑ξ′∈sl′∑[γl+fr(ξ)−fr(ξ′)]+.
总损失
l = l e + l c + l l \mathcal{l}=\mathcal{l_{e}}+\mathcal{l_{c}}+\mathcal{l_{l}} l=le+lc+ll
训练集
对于一个真实的关系三元组 ( h , r , t ) (h,r,t) (h,r,t),通过替换 h h h或 t t t为 h ′ h' h′或 t ′ t' t′来生成负例,其中 h ′ h' h′是从集合 m t = m 1 ∪ m 2 … m n \mathcal{m_{t}}=\mathcal{m_{1}} \cup \mathcal{m_{2}} \dots \mathcal{m_{n}} mt=m1∪m2…mn中随机挑选的,其中 m i = { a ∣ a ∈ i ∧ ( a , r e , c i ) ∈ s e ∧ ( t , r e , c i ) ∈ s e ∧ t ≠ a } m_{i}=\{a|a\in i \wedge (a,r_{e},c_{i})\in \mathcal{s_{e}} \wedge (t,r_{e},c_{i}) \in \mathcal{s_{e}} \wedge t \neq a \} mi={a∣a∈i∧(a,re,ci)∈se∧(t,re,ci)∈se∧t=a},也就是从把头实体或者是尾实体换成相同概念的实体或者是不同概念的实体。
生成策略包括:
- 均匀采样
- 伯努利采样:基于链接头尾实体数目栏进行采样,数目多的实体被采样的概率更大。
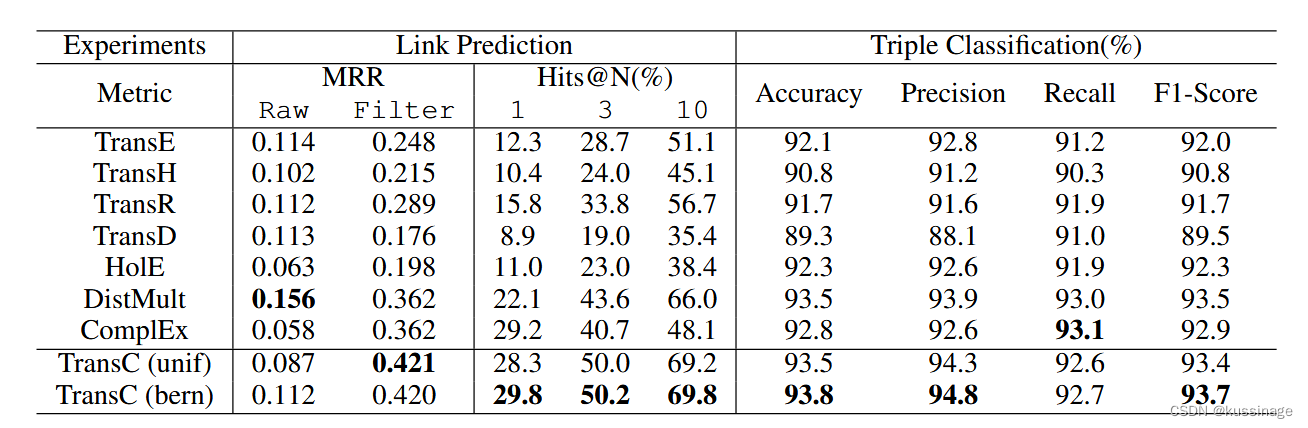
实验
对链接预测和三元组分类进行实验







发表评论