目录
一、概念
1、概念
决策树分二叉树和非二叉树,通过分析某些特征对数据集进行划分,从而预测新的待测样本。简单来说就是想象一棵树,根节点代表我们对数据集特征选取,而树枝和叶子代表在特征属性下对数据集的不同判断和结果。
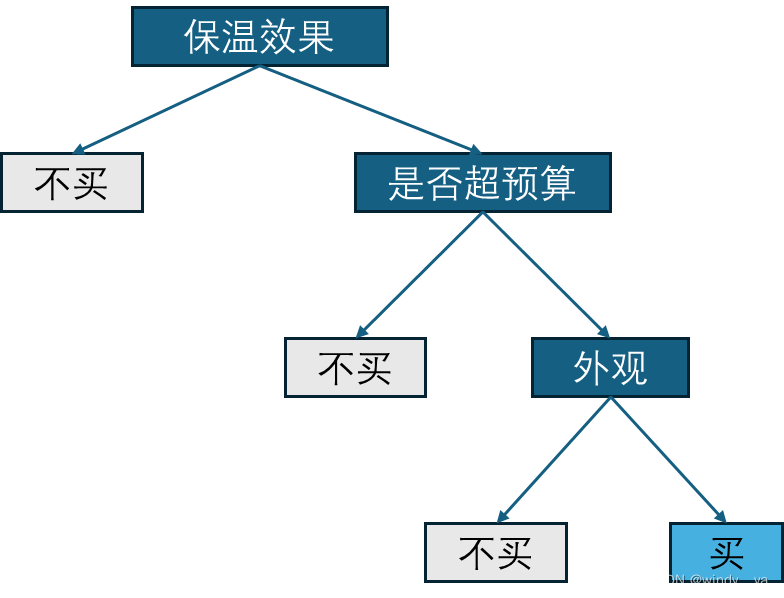
2、结束条件
(1)没有特征可以往下分了
(2)剩下的样本都属于同一个类别
(3)剩下的样本数少于设定的阈值
(4)达到设定的深度
3、熵
那么决策树如何构建?怎么决定哪个特征先判断?——由此,引出熵这个概念,即表示不确定性、混乱程度。熵越大越混乱。
熵的表达式为: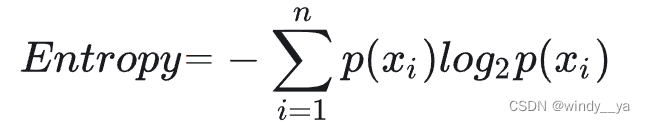
后续计算信息增益/增益率需要用到信息熵。
二、算法&具体例题计算
1、id3信息增益
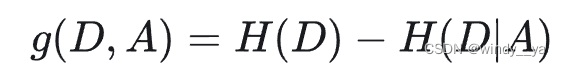
1)计算集合d的信息熵h(d):
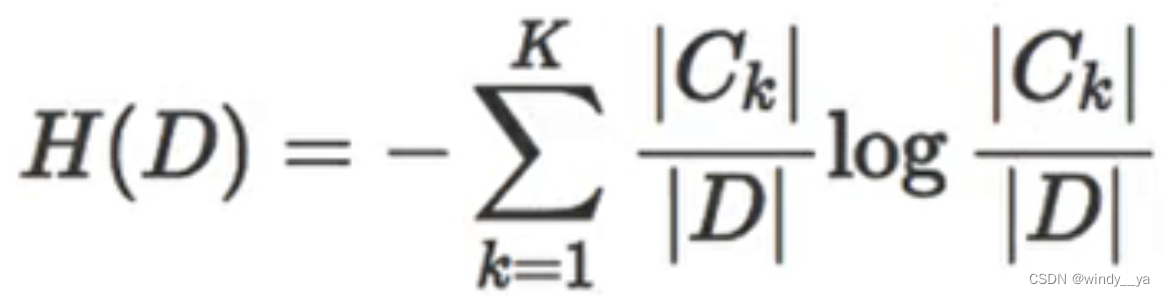
2)计算特征a条件下d的信息熵h(d|a),即a的影响程度大不大:
![]()
3)最后算差值计算信息增益:gain(d,a) = h(d) - h(a)
2、c4.5 信息增益率
其实就是上面的信息增益 / 特征a的信息熵:
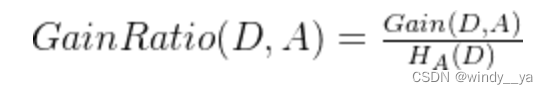
3、基尼指数
基尼指数越小纯度越高。
1)计算整个样本d的基尼指数:
![]()
2)计算在特征a的条件下集合d的基尼指数,即a用于判断集合d的影响:
![]()
3)最后选择基尼指数较小的特征进行划分。
二-一 例题
下面举个具体的例子来说明这三个算法的决策树构建:
| 样本 | 属性 | 分类 | |
| x1 | x2 | ||
| 1 | t | t | √ |
| 2 | t | f | √ |
| 3 | t | f | × |
| 4 | f | t | √ |
| 5 | f | t | × |
| 6 | f | t | √ |
(1)id3信息增益:
h(d) = -(4/6)log(4/6) - (2/6)log(2/6) =0.918
h(t1) = -(2/3)log(2/3) - (1/3)log(1/3) = 0.918
h(f1) = -(2/3)log(2/3) - (1/3)log(1/3) = 0.918
gain(d,x1) = h(d) - [ (1/2)h(t1) + (1/2)h(f1) ] = 0
h(t2) = -(3/4)log(3/4)-(1/4)log(1/4) = 0.811
h(f2) = -(1/2)log(1/2) - (1/2)log(1/2) = 1
gain(d,x2) =h(d) -[ (4/6)h(t2) + (2/6)h(f2) ] = 0.918-0.874 = 0.044
0.044>0,选x2为第一个特征。
(2)gini

0.444>0.417,基尼指数越小纯度越高所以选x2作为划分特征。
三、python实例
1、基尼指数
(1)构建gini代码计算acc
import numpy as np
import torchvision
import torchvision.transforms as transforms
from torchvision import datasets
from sklearn import tree
def load_date():
transform = transforms.compose([transforms.totensor(),transforms.normalize((0.1307, ),(0.3081, ))])
dataset_train = datasets.mnist(root='../data/minist',train=true,download=true,transform=transform)
dataset_test = datasets.mnist(root='../data/minist',train=false,download=true,transform=transform)
x_train = dataset_train.data.numpy()
x_test = dataset_test.data.numpy()
x_train = np.reshape(x_train,(60000,784))
x_test =np.reshape(x_test,(10000,784))
y_train = dataset_train.targets.numpy()
y_test = dataset_test.targets.numpy()
return x_train,y_train,x_test,y_test
if __name__ == '__main__':
train_x,train_y,test_x,test_y = load_date()
cart = tree.decisiontreeclassifier(criterion='gini',max_depth=8,random_state=5)
# cart = tree.decisiontreeclassifier(criterion='entropy',max_depth=8)
cart = cart.fit(train_x,train_y)
acc = cart.score(test_x,test_y)
print("准确率:",acc)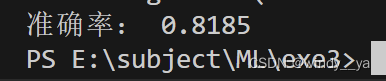
(2)决策树可视化
#可视化
plt.figure(figsize=(12.8, 6.4))
plt.subplot(121)
tree.plot_tree(cart)
plt.title("gini")
plt.show()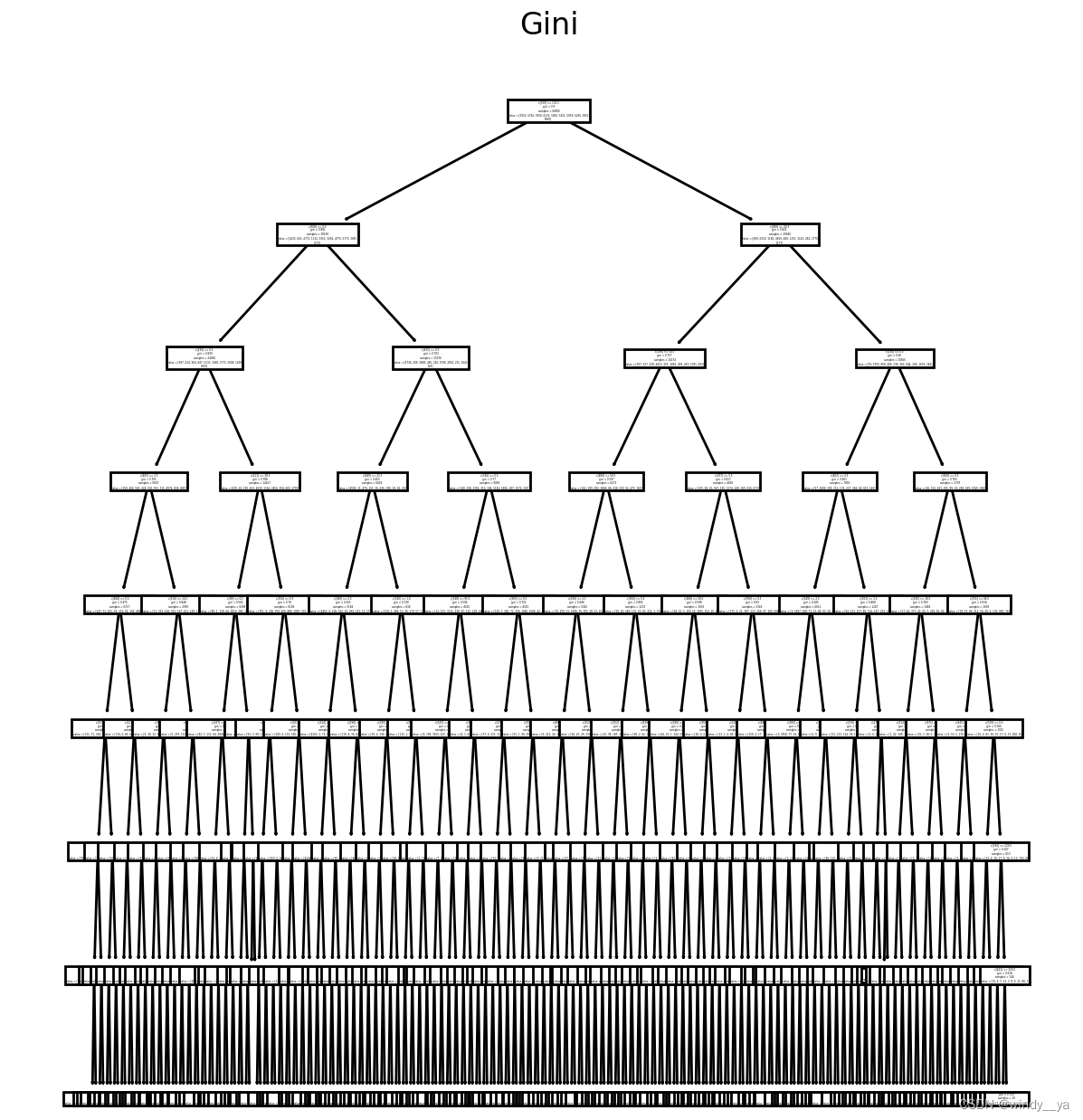
2、id3信息增益
(1)构建id3代码计算acc
if __name__ == '__main__':
train_x,train_y,test_x,test_y = load_data()
# cart = tree.decisiontreeclassifier(criterion='gini',max_depth=3,random_state=5)
cart = tree.decisiontreeclassifier(criterion='entropy',max_depth=8)
cart = cart.fit(train_x,train_y)
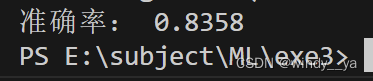
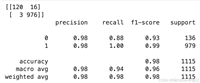
acc = cart.score(test_x,test_y)
print("准确率:",acc)
(2)决策树可视化
#可视化
plt.figure(figsize=(12.8, 6.4))
plt.subplot(121)
tree.plot_tree(cart)
plt.title("id3")
plt.show()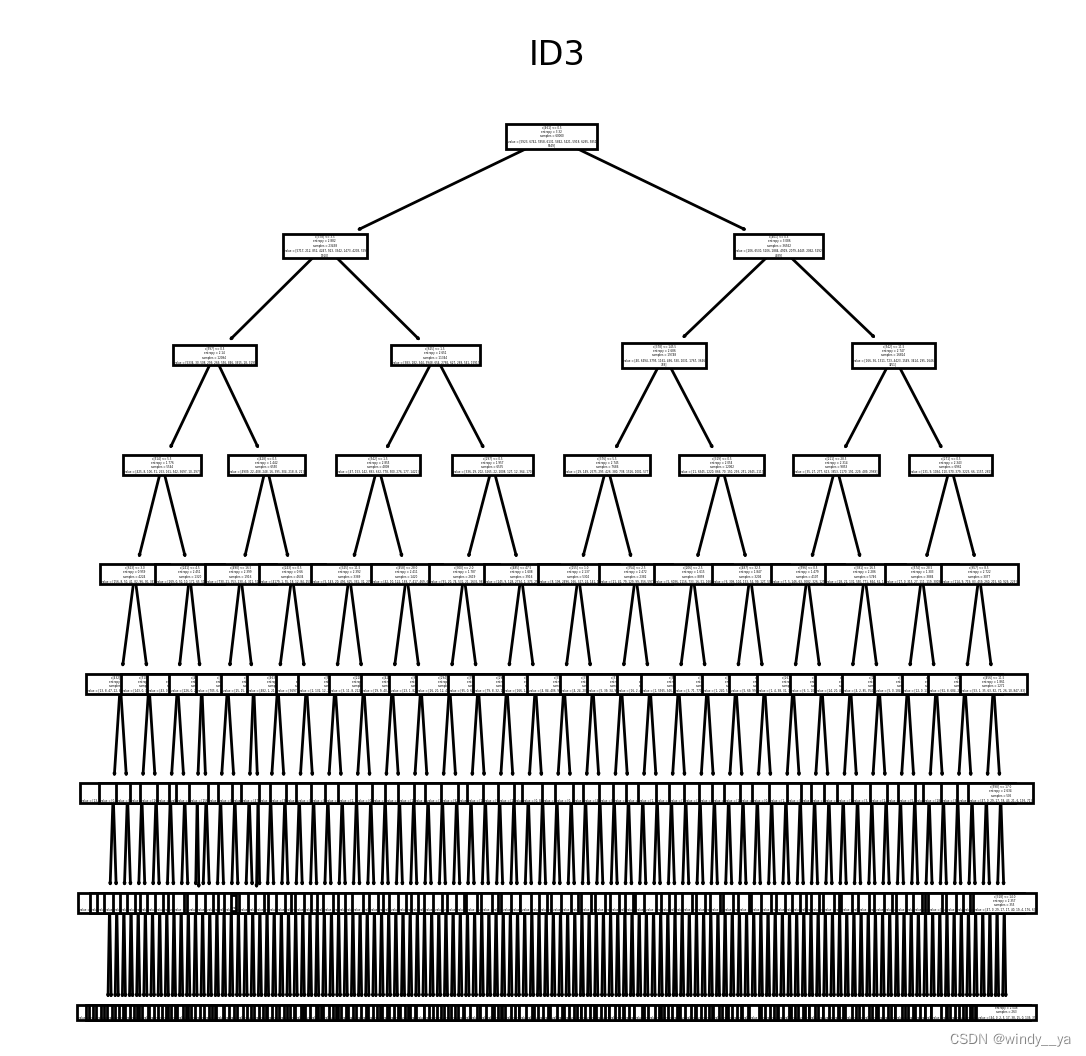


发表评论