决策树
图中的决策树呈现自顶向下的生长过程,深色的椭圆表示树的根节点;浅色的椭圆表示树的中间节点;方框则表示树的叶节点。
对于所有的非叶节点来说,都是用来表示条件判断,而叶节点则存储最终的分类结果,例如中年分支下的叶节点(4,0)表示4位客户购买,0位客户不购买。

决策树节点字段的选择
信息熵
我们首先了解下信息熵
熵原本是物理学中的一个定义,后来香农将其引申到了信息论领域,用来表示信息量的大小。信息量越大(分类越不“纯净”),对应的熵值就越大,反之亦然。也就是信息量大,熵大,一个事件发生的概率小,反之亦然。信息熵的计算公式如下:

在实际应用中,会将概率p的值用经验概率替换,所以经验信息可以表示为:

举个例子:以产品是否被购买为例,假设数据集一共包含14个样本,其中购买的用户有9个,没有购买的用户有5个,所以对于是否购买这个事件来说,它的经验信息为:
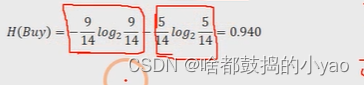
条件熵
判断在某个条件下的信息熵为条件熵


比如:
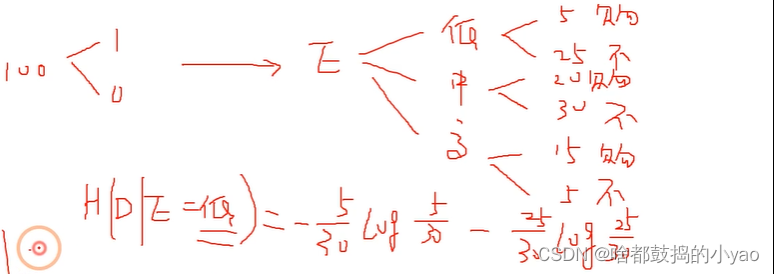
信息增益
对于已知的事件a来说,事件d的信息增益就是d的信息熵与a事件下d的条件熵之差,事件a对事件d的影响越大,条件熵h(d|a)就会越小(在事件a的影响下,事件d被划分得越“纯净”),体现在信息增益上就是差值越大,进而说明事件d的信息熵下降得越多。
所以,在根节点或中间节点的变量选择过程中,就是挑选出各自变量下因变量的信息增益最大的。

其中:d是事件y的所有可能
信息增益率
决策树中的id3算法使用信息增益指标实现根节点或中间节点的字段选择,但是该指标存在一个非常明显的缺点,即信息增益会偏向于取值较多的字段。
为了克服信息增益指标的缺点,提出了信息增益率的概念,"它的思想很简单,就是在信息增益的基础上进行相应的惩罚。信息增益率的公式可以表示为:

其中,ha为事件a的信息熵。事件a的取值越多,gaina(d)可能越大,但同时ha也会越大,这样以商的形式就实现了gaina(d)的惩罚。
基尼指数
决策树中的c4.5算法使用信息增益率指标实现根节点或中间节点的字段选择,但该算法与id3算法致,都只能针对离散型因变量进行分类,对于连续型的因变量就显得束手无策了。
为了能够让决策树预测连续型的因变量,breiman等人在1984年提出了cart算法,该算法也称为分类回归树,它所使用的字段选择指标是基尼指数。
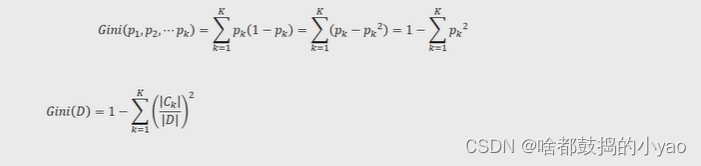
条件基尼指数

基尼指数增益
与信息增益类似,还需要考虑自变量对因变量的影响程度,即因变量的基尼指数下降速度的快慢,下降得越快,自变量对因变量的影响就越强。下降速度的快慢可用下方式子衡量:
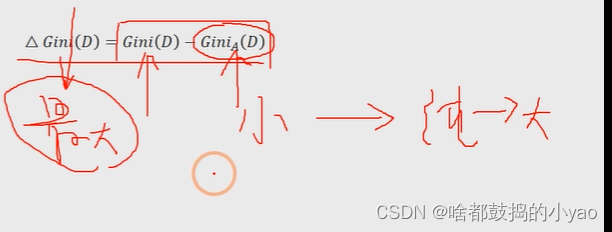
决策树函数
随机森林
利用bootstrap抽样法,从原始数据集中生成k个数据集,并且每个数据集都含有n个观测和p个自变量。
针对每一个数据集,构造一棵cart决策树,在构建子树的过程中,并没有将所有自变量用作节点字段的选择,而是随机选择p个字段。
让每一棵决策树尽可能地充分生长,使得树中的每个节点尽可能“纯净”,即随机森林中的每一棵子树都不需要剪枝。
针对k棵cart树的随机森林,对分类问题利用投票法,将最高得票的类别用于最终的判断结果;对回归问题利用均值法,将其用作预测样本的最终结果。
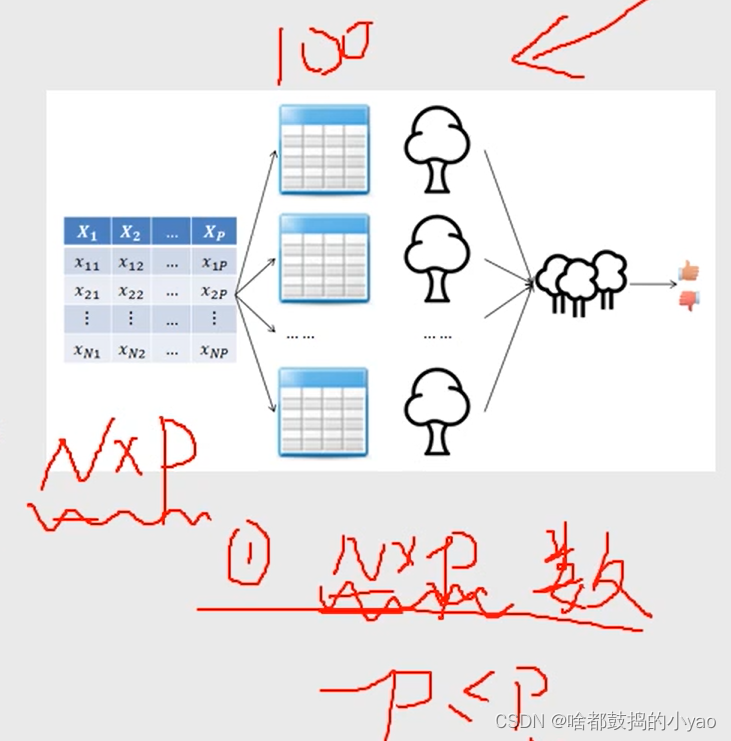
生成100个树,每个数据集为一个树


发表评论