哈希
哈希本质上还是一个数组,只是数组的每一个位置要存储的值进行了映射;
哈希也可以叫做散列;
哈希比红黑树快是因为,不需要重复进行比较大小,直接用映射关系进行查找;
哈希函数的设计应该注意要减少哈希冲突;
1.unordered系列关联式容器的使用
java设计的是hashmap与hashset,treemap与treeset。
stl的map与set的底层是红黑树,unorderedmap与unorderedset的底层设计的是哈希表/桶;
与map/set的区别是,1.迭代器使用的都是单向迭代器;2.遍历出来不是有序的,只能去重;3.哈希表的性能比起红黑树更高一些;
注意插入重复数据时哈希更快,非重复时红黑树更快,其他如查找,删除都是哈希更快。
对于有序数据还是红黑树更快,包括插入,查找,删除;
1.1unordered_set
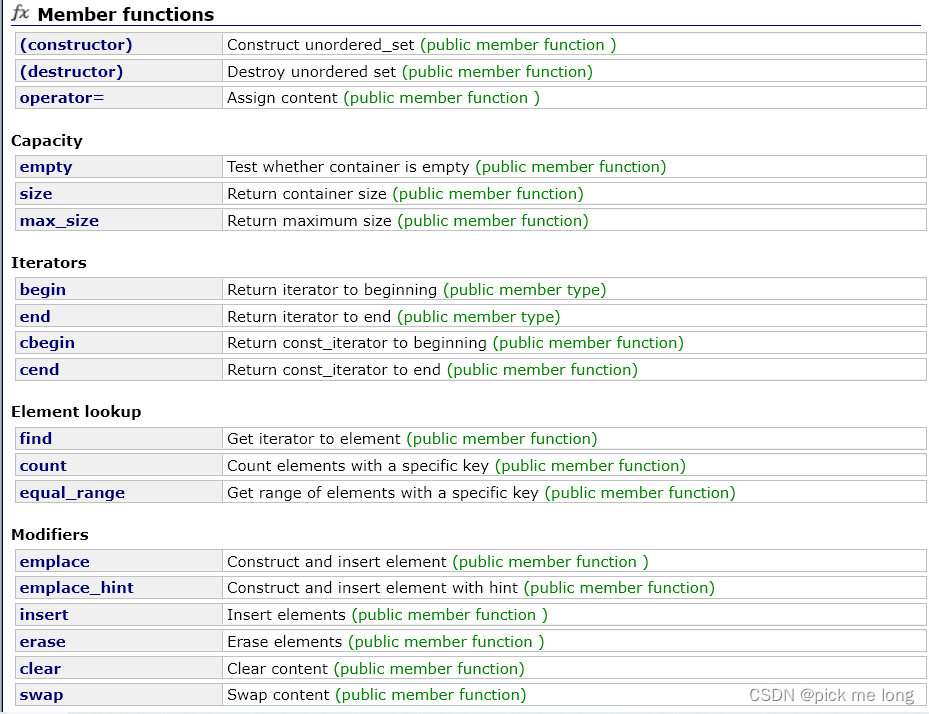

1.2unordered_map
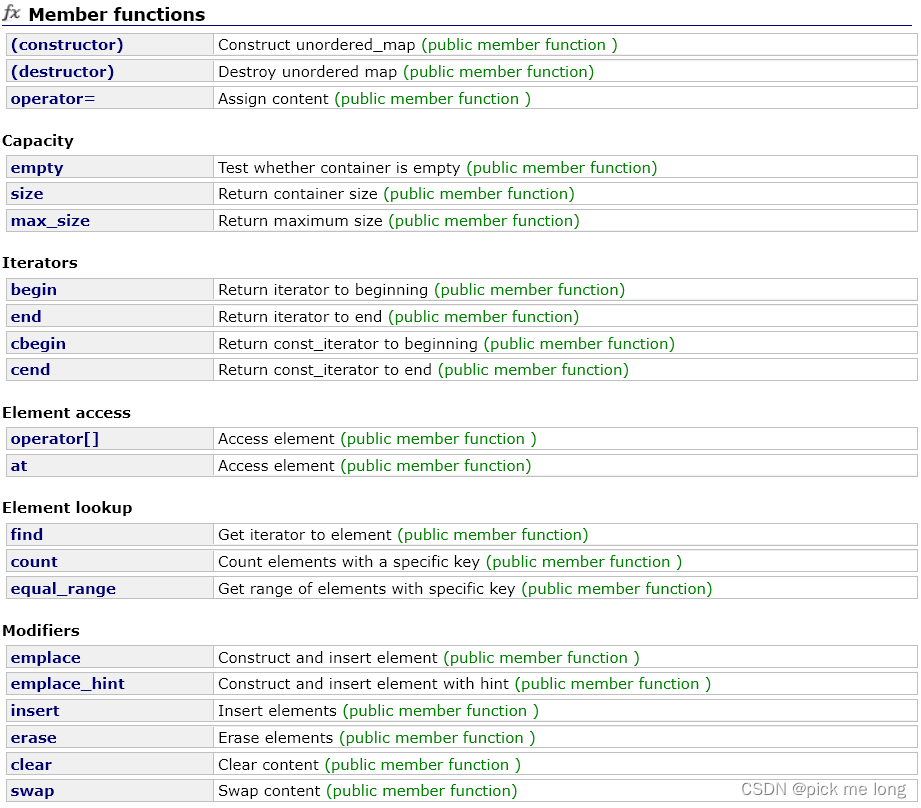

2.不同查找方式的对比
1.暴力查找时间按复杂度o(n);
2.有序数组的二分查找o(lgn),存在排序o(n*logn)和增删改需要挪动数据o(n)的问题。
3.平衡搜索树o(lgn),天然有序,增删查改也比较方便;
4.哈希(散列)存储的值和存储的位置建立一个对应关系,根据对应关系进行快速查找;
3.哈希
1.计数排序使用的就是一种哈希;
2.图书馆找书,根据字母排序进行哈希查找相关书籍;
如果数据很分散,那就退化成了暴力查找;
3.1常见的哈希函数
1.直接定址法,使用直接映射查找,一对一,适合数据集中使用,问题:数据分散就会退化成暴力查找;
2.除留余数法,开辟capacity个位置的空间,int i = k % capacity,然后将key放到第i个位置,问题:会产生哈希冲突/碰撞,即不同的值可能会映射到同一个位置,值和位置的关系是多对一的关系;
如果是整型直接进行映射,如果是对象或者字符串就需要先与整数进行映射,然后在用整数和位置进行映射;
3.2解决哈希冲突
1.闭散列的开放定址法,缺陷是冲突会互相影响,如连续空间的值会互相影响;
思路是:位置被占了,就找下一个位置(本质上找的是别人的位置),会造成踩踏拥堵;
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止,空间不够会进行扩容;
问题是:1.会不断的抢占位置;2.哈希表不能太满,否则会导致下降,所以是不可能找不到空位置的;3.删除会导致查找出错,所以需要存在三个状态标记,1.exist,2.empty,3.delete ;
二次探测,与线性探测唯一的区别就是每次移动走的是平方,1 4 9 …,好处是每次查找的时候不是走连续的空间,若一段连续空间内存在多个值,就会降低哈希冲突的概率;
2.开散列的拉链法(哈希桶):
在原有顺序表的位置使用类似链表的方式,在顺序表外将多个值链接在此位置之后;
4.线性探测实现哈希表
1.使用枚举变量,来控制状态;2.对于哈希数据要存放kv和状态枚举变量;3.对于哈希表使用vector来开辟空间存放哈希数据,使用size记录有效数据;4.设计负载因子,负载因子为表中的元素个数除以长度;
对于插入函数的设计,1.要注意负载因子越大,产生哈希冲突的概率越大,但是空间利用率更高,所以综合一下控制负载因子到一定值就扩容,不能满了才扩容或空间利用率过低;2.扩容先计算新的空间大小,然后重新开辟一个哈希表,并且使用resize使得大小和空间相同,遍历旧表插入新表,然后交换新旧表;3.使用除留余数法来获取顺序表的下标;4…不断线性探测空位置;5.找到了空位置,插入哈希数据,设置kv并修改状态变量;
对于删除函数的设计,较为简单先find,然后置为delete并且size–。
由于映射使用的是下标位置是自然数,所以要注意对于非无符号整型要先建立无符号整型映射,推荐使用仿函数;对于常见的类型可以使用模板的特化;如果只是使用字符转整型相加还是右很多场景得到的值相同,难以避免哈希冲突,所以需要使用哈希算法bkdr算法,即每次加之前乘131,使用131是因冲突数相较于其他算法较少;
代码实现:
#pragma once
#include <vector>
namespace hashtable
{
enum status
{
exist = 0,
empty,
delete,
};
template <class k, class v>
struct hashdata
{
std::pair<k, v> kv_;
status status_ = empty;
};
template <class k>
struct default
{
size_t operator()(const k &key)
{
return (size_t)key;
}
};
template <>
struct default<std::string>
{
size_t operator()(const std::string &key)
{
size_t i = 0;
for (const auto &ch : key)
{
i *= 131;
i += ch;
}
return i;
}
};
// struct stringfunc
// {
// size_t operator()(const std::string& key)
// {
// return key[0];
// }
// };
template <class k, class v, class hashfunc = default<k>>
class hashtable
{
public:
hashtable()
{
table_.resize(10); // 使用resize保证size和capacity的值是一样的
}
bool insert(const std::pair<k, v> &kv) // 要注意不可以使得这个表太满,否则会降低查找效率,甚至表满了会不断死循环下去
{
if (find(kv.first))
{
return false;
}
hashfunc func;
// 扩容逻辑,要注意的是扩容完成之后映射关系会发生改变,因为扩容后除数变大了
if ((double)size_ / (double)table_.size() >= 0.7)
{
size_t newsize = table_.size() * 2;
hashtable<k, v, hashfunc> hashtable;
hashtable.table_.resize(newsize);
// 遍历旧表重新插入到新表
for (const auto &e : table_)
{
if (e.status_ == exist)
{
hashtable.insert(e.kv_);
}
}
// 交换新旧表
table_.swap(hashtable.table_);
}
// 线性探测
size_t hashi = func(kv.first) % table_.size(); // 不能%capacity因为断言检查的是size,会有越界风险,最好是使得size与capacity相等
// 如果这个位置存在值,就需要探测到空停止
if (func(table_[hashi].kv_.first) != func(kv.first))
{
while (table_[hashi].status_ == exist)
{
hashi++;
hashi %= table_.size();
}
// 找到了空位置进行插入
table_[hashi].kv_ = kv;
table_[hashi].status_ = exist;
size_++;
return true;
}
else
{
return false;
}
}
hashdata<const k, v> *find(const k &key)
{
default<k> func;
size_t hashi = func(key) % table_.size();
while (table_[hashi].status_ != empty) // 由于delete状态可能是数据再后面位置,不能停止
{
if (table_[hashi].status_ != delete && table_[hashi].kv_.first == key)
{
return (hashdata<const k, v> *)&table_[hashi]; // 会产生隐式类型转化,有的编译器不支持需要显式转换
}
hashi++;
hashi %= table_.size();
}
return nullptr;
}
bool erase(const k &key)
{
hashdata<const k, v> *pos = find(key);
if (pos)
{
pos->status_ = delete;
size_--;
return true;
}
return false;
}
private:
std::vector<hashdata<k, v>> table_; // 物理空间上就是一个是顺序表,逻辑上是一个哈希
size_t size_ = 0; // 存放有效数据的个数
};
}



发表评论