
🎬慕斯主页:
♈️今日夜电波:消えてしまいそうです—真夜中
1:15━━━━━━️💟──────── 4:18
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
一、二叉搜索树概念
什么是二叉搜索树?
如下便是一颗二叉搜索树:
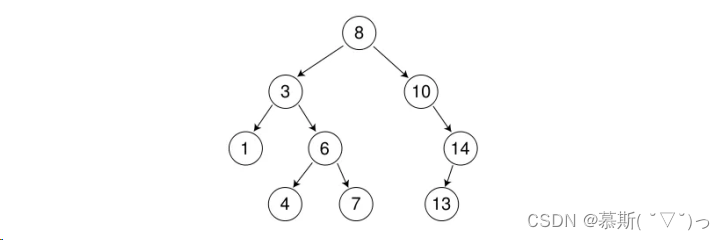
二叉搜索树的基本操作

二、二叉搜索树的实现
节点的定义
//节点定义
template<class k>
struct bstreenode
{
bstreenode<k>* _left;
bstreenode<k>* _right;
k _key;
bstreenode(const k& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
二叉搜索树的定义
//二叉搜索树
template<class k>
class bstree
{
typedef bstreenode<k> node;
public:
//...诸多的操作
private:
node* _root = nullptr;
};
非递归操作
插入操作
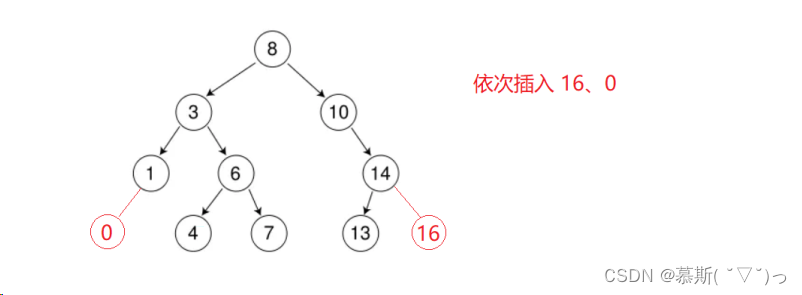
//插入操作,按照左小右大的规则
bool insert(const k& key)
{
if (_root == nullptr)
{
_root = new node(key);
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
查找操作
//查找操作
bool find(const k& key)
{
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
删除操作(重点及难点!!!)
现在详细介绍这两种情况:
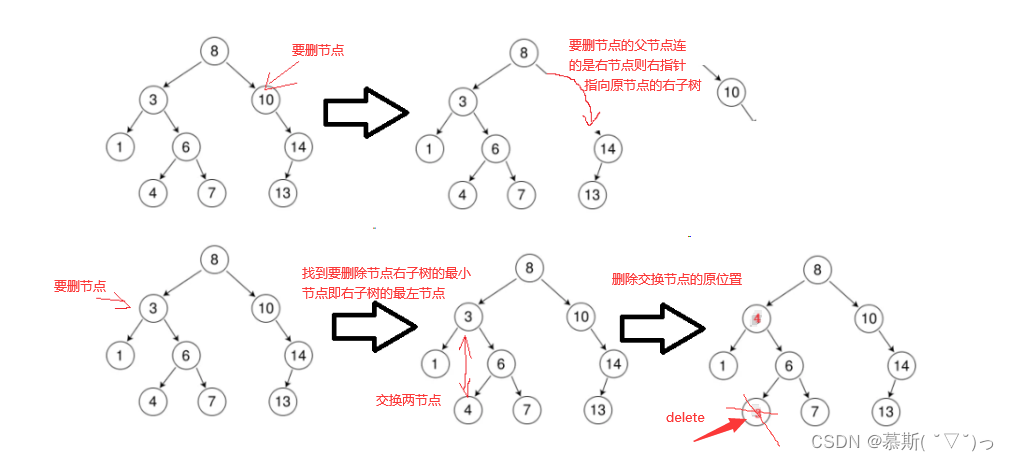
实现如下:
bool erase(const k& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else//表示已经找到,进行删除操作
{
//左为空的情况
if (cur->_left == nullptr)
{
if (cur == _root)//要删即为根节点
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)//因为左一定为空,为父节点的左则将右半边给父即可
{
parent->_left = cur->_right;
}
else//同理为父节点的右则将右半边给父
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)//右为空的情况
{
//同理左为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//左右都不为空
{//可以选择找该节点左子树的最大节点(最右节点)或者右子树的最小节点(最左节点)
//这里找右树的最小节点(最左节点)
node* parent = cur;
node* subleft = cur->_right;
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->_key, subleft->_key);
//由于找到的是最左,则默认左为空,所以只需将右链接给父节点
if (subleft == parent->_left)
{
parent->_left = subleft->_right;
}
else
{
parent->_right = subleft->_right;
}
delete subleft;
}
return true;
}
}
return false;
}
递归法操作
中序遍历排升序(经典操作!)
void _inorder(node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_key << " ";
_inorder(root->_right);
}
插入操作(递归)
bool _insertr(node*& root, const k& key)
{
if (root == nullptr)
{
root = new node(key);
return true;
}
if (root->_key < key)
return _insertr(root->_right, key);
else if (root->_key > key)
return _insertr(root->_left, key);
else
return false;
}
查找操作(递归)
bool _findr(node* root, const k& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _findr(root->_right, key);
}
else if (root->_key > key)
{
return _findr(root->_left, key);
}
else
{
return true;
}
}
删除操作(递归)
bool _eraser(node*& root, const k& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _eraser(root->_right, key);
}
else if (root->_key > key)
{
return _eraser(root->_left, key);
}
else//找到了开始删除
{
//实际上的操作同非递归差不多,这里巧妙的对root运用了引用
if (root->_left == nullptr)
{
node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
node* del = root;
root = root->_left;
delete del;
return true;
}
else//找右子树的最大
{
node* subleft = root->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
swap(root->_key, subleft->_key);
// 转换成在子树去递归删除
return _eraser(root->_right, key);
}
}
}
二叉搜索树的应用
kv模型二叉搜索树
namespace kv
{
template<class k, class v>
struct bstreenode
{
bstreenode<k, v>* _left;
bstreenode<k, v>* _right;
k _key;
v _value;
bstreenode(const k& key, const v& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class k, class v>
class bstree
{
typedef bstreenode<k, v> node;
public:
bool insert(const k& key, const v& value)
{
if (_root == nullptr)
{
_root = new node(key, value);
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
node* find(const k& key)
{
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool erase(const k& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除 20:15继续
if (cur->_left == nullptr)
{//左为空
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
else if (cur->_right == nullptr)
{//右为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else
{//左右都不为空
// 右树的最小节点(最左节点)
node* parent = cur;
node* subleft = cur->_right;
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->_key, subleft->_key);
if (subleft == parent->_left)
parent->_left = subleft->_right;
else
parent->_right = subleft->_right;
}
return true;
}
}
return false;
}
void inorder()
{
_inorder(_root);
cout << endl;
}
private:
void _inorder(node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_inorder(root->_right);
}
private:
node* _root = nullptr;
};
}
三、整体代码
#pragma once
#include<iostream>
using namespace std;
namespace k
{
//节点定义
template<class k>
struct bstreenode
{
bstreenode<k>* _left;
bstreenode<k>* _right;
k _key;
bstreenode(const k& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
//二叉搜索树
template<class k>
class bstree
{
typedef bstreenode<k> node;
public:
//插入操作,按照左小右大的规则
bool insert(const k& key)
{
if (_root == nullptr)
{
_root = new node(key);
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//查找操作
bool find(const k& key)
{
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool erase(const k& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else//表示已经找到,进行删除操作
{
//左为空的情况
if (cur->_left == nullptr)
{
if (cur == _root)//要删即为根节点
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)//因为左一定为空,为父节点的左子树则将右半边给父即可
{
parent->_left = cur->_right;
}
else//同理为父节点的右则将右半边给父
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)//右为空的情况
{
//同理左为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//左右都不为空
{//可以选择找该节点左子树的最大节点(最右节点)或者右子树的最小节点(最左节点)
//这里找右树的最小节点(最左节点)
node* parent = cur;
node* subleft = cur->_right;
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->_key, subleft->_key);
//由于找到的是最左,则默认左为空,所以只需将右链接给父节点
if (subleft == parent->_left)
{
parent->_left = subleft->_right;
}
else
{
parent->_right = subleft->_right;
}
delete subleft;
}
return true;
}
}
return false;
}
void inorder()//中序遍历即排升序
{
_inorder(_root);
cout << endl;
}
bool findr(const k& key)//递归找
{
return _findr(_root, key);
}
bool insertr(const k& key)//递归插入
{
return _insertr(_root, key);
}
bool eraser(const k& key)//递归删
{
return _eraser(_root, key);
}
bstree() = default;// c++11
~bstree()
{
destroy(_root);
}
bstree(const bstree<k>& t)
{
_root = copy(t._root);
}
// t1 = t3
bstree<k>& operator=(bstree<k> t)
{
swap(_root, t._root);
return *this;
}
private:
node* copy(node* root)
{
if (root == nullptr)
return nullptr;
node* newroot = new node(root->_key);
newroot->_left = copy(root->_left);
newroot->_right = copy(root->_right);
return newroot;
}
void destroy(node*& root)
{
if (root == nullptr)
return;
destroy(root->_left);
destroy(root->_right);
delete root;
root = nullptr;
}
bool _eraser(node*& root, const k& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _eraser(root->_right, key);
}
else if (root->_key > key)
{
return _eraser(root->_left, key);
}
else//找到了开始删除
{
//实际上的操作同非递归差不多,这里巧妙的对root运用了引用
if (root->_left == nullptr)
{
node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
node* del = root;
root = root->_left;
delete del;
return true;
}
else//找右子树的最大
{
node* subleft = root->_right;
while (subleft->_left)
{
subleft = subleft->_left;
}
swap(root->_key, subleft->_key);
// 转换成在子树去递归删除
return _eraser(root->_right, key);
}
}
}
bool _insertr(node*& root, const k& key)
{
if (root == nullptr)
{
root = new node(key);
return true;
}
if (root->_key < key)
return _insertr(root->_right, key);
else if (root->_key > key)
return _insertr(root->_left, key);
else
return false;
}
bool _findr(node* root, const k& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _findr(root->_right, key);
}
else if (root->_key > key)
{
return _findr(root->_left, key);
}
else
{
return true;
}
}
void _inorder(node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_key << " ";
_inorder(root->_right);
}
node* _root = nullptr;
};
}
namespace kv
{
template<class k, class v>
struct bstreenode
{
bstreenode<k, v>* _left;
bstreenode<k, v>* _right;
k _key;
v _value;
bstreenode(const k& key, const v& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class k, class v>
class bstree
{
typedef bstreenode<k, v> node;
public:
bool insert(const k& key, const v& value)
{
if (_root == nullptr)
{
_root = new node(key, value);
return true;
}
node* parent = nullptr;
node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
node* find(const k& key)
{
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool erase(const k& key)
{
node* parent = nullptr;
node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除 20:15继续
if (cur->_left == nullptr)
{//左为空
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
else if (cur->_right == nullptr)
{//右为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else
{//左右都不为空
// 右树的最小节点(最左节点)
node* parent = cur;
node* subleft = cur->_right;
while (subleft->_left)
{
parent = subleft;
subleft = subleft->_left;
}
swap(cur->_key, subleft->_key);
if (subleft == parent->_left)
parent->_left = subleft->_right;
else
parent->_right = subleft->_right;
}
return true;
}
}
return false;
}
void inorder()
{
_inorder(_root);
cout << endl;
}
private:
void _inorder(node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_inorder(root->_right);
}
private:
node* _root = nullptr;
};
}
感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~


发表评论