【深度学习】GAN生成对抗网络原理推导+代码实现（Python）

1、前言

本文将讲近些年来挺火的一个生成模型$\boxed{\mathbf{gan}\mathbf{生成对抗网络}}$，其特殊的思路解法实在让人啧啧称奇。
数学基础：【概率论与数理统计知识复习-哔哩哔哩】
视频：【生成对抗网络gan原理解析-哔哩哔哩】

2、原理

2.1、gan的运行机理

在传统的生成模型中，我们总是对我们的训练数据（或观测变量和隐变量）进行建模，得到概率分布，然后进行数据的生成。可gan却不是这样，其利用神经网络这个函数逼近器，求解出了模型中概率分布的参数$\boxed{在不知道概率分布是什么的情况下}$。

其主要思想是，从一个简单的概率分布中采样，得到样本经过神经网络变换，得到一个新的样本，我们就假设这个样本就来自我们需要求解的概率分布中。然后用神经网络去辨别其是来自真实分布，还是我们要求解的概率分布。

先来看模型图

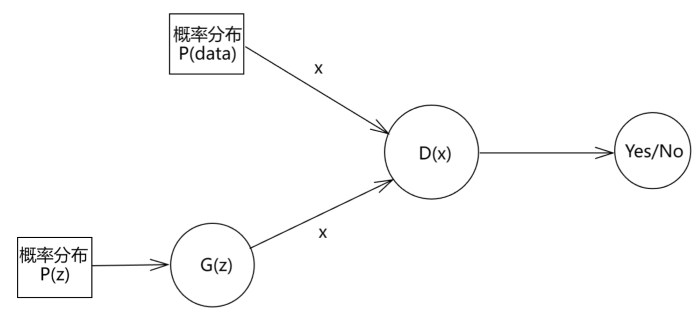
我们的训练数据$x$是来自真实分布$\boxed{\mathbf{对应图中}\mathbf{p}(\mathbf{data})}$，我们记作$p_{data}$，训练数据都是从$p_{data}$中采样得来（图中上半部分的x）。

而我们从简单的概率分布中抽样$p(z)$$\boxed{\mathbf{如正态分布}}$，让所得的样本经过一个神经网络$g(z)$，得到一个新的样本$x$，这个样本就来自我们的需要求解的概率分布，我们记作$p_g$。

然后将两个x给神经网络$d(x)$判断真伪，让它区分这个x是来自$p_{data}$还是$p_g$，其输出样本来自$p_{data}$的概率。依据所得信息使用梯度下降更新神经网络参数，$g(z)$也是如此。

而$g(z)$被称为生成器$\boxed{(\mathbf{用于生成样本})}$，$d(x)$被称为判别器$\boxed{\mathbf{用于判别样本真伪}}$。

2.2、目标函数

$\boxed{\mathbf{损失函数来自判别器和生成器}}$

$\boxed{对于判别器}$

当样本来自$p_{data}$，我们要让所得的概率越大越好；当样本来自$p_g$，我们要让其概率越小越好，即
$$\begin{gathered} ①\underset{d}{\max }d(x_i) \\ ②\underset{d}{\min }d(g(z_i)) \end{gathered}$$
将最小化换成最大化
$$\underset{d}{\max }[1-d(g(z_i))]$$
所以单个样本判别器的损失函数可以写成
max ⁡ d { d ( x i ) + [ 1 − d ( g ( z i ) ) ] } \max\limits_{d}\left\{d(x_i)+[1-d(g(z_i))]\right\} dmax​{d(xi​)+[1−d(g(zi​))]}
对于所有样本n，我们希望均值最大
$$\underset{d}{\max }\left\{\frac{1}{n}\sum _{i=1}^{n}d(x_i)+\frac{1}{n}\sum _{i=1}^n[1-d(g(z_i))]\right\}$$
写成期望形式（并取log最大$\boxed{不改变最大值}$），得到判别器的损失函数（$x\sim p_{data}$表示样本来自真实分布，$p_z$表示正态分布）
max ⁡ d { e x ∼ p d a t a [ log ⁡ d ( x ) ] + e z ∼ p z [ log ⁡ ( 1 − d ( g ( z ) ) ) ] } \boxed{\max\limits_{d}\left\{\mathbb{e}_{x\sim p_{data}}\left[\log d(x)\right]+\mathbb{e}_{z\sim p_z}\left[\log(1-d(g(z)))\right]\right\}} dmax​{ex∼pdata​​[logd(x)]+ez∼pz​​[log(1−d(g(z)))]}​
接着，我们在上面讲到过，g(z)表示的是，采用一个z，经过一个神经网络，得到一个伪造出来的x。这个伪造的x服从分布$p_g$。那么我们就可以把第二个期望改写成x的表达式，于是便可得到
$$\boxed{\underset{d}{\max }\left\{{\mathbb{e}}_{x\sim p_{data}}\left[\log d(x)\right]+{\mathbb{e}}_{x\sim p_g}\left[\log (1-d(x))\right]\right\}}$$
$\boxed{对于生成器}$

它希望生成的样本让判别器判别为真的概率越大越好，所以直接设计成（将最大写成最小）
$$\boxed{\underset{g}{\min }{\mathbb{e}}_{x\sim p_g}\left[\log (1-d(x))\right]}$$
所以最终的目标函数可以写成
$$\underset{g}{\min }\underset{d}{\max }\left\{{\mathbb{e}}_{x\sim p_{data}}\left[\log d(x)\right]+{\mathbb{e}}_{x\sim p_g}\left[\log (1-d(x))\right]\right\}$$

3、最优解求解

得到了目标函数，我们很显然还需要证明其存在最优解。并且最优解的$p_g$是否和$p_{data}$无限接近

$\boxed{先求里层（关于d求最大）}$
$$\begin{array}{rl}& {\mathbb{e}}_{x\sim p_{data}}\left[\log d(x)\right]+{\mathbb{e}}_{x\sim p_g}\left[\log (1-d(x))\right]\\ =& {\int }_x\log d(x)p_{data}(x)dx+{\int }_x\log (1-d(x))p_g(x)dx\\ =& {\int }_x\left[\log d(x)p_{data}(x)+\log (1-d(x))p_g(x)\right]dx\end{array}$$
要求积分最大，就是要求里面的每一个最大
$$\underset{d}{\max }\left[\log d(x)p_{data}(x)+\log (1-d(x))p_g(x)\right]$$
求导
$$\begin{array}{rl}& \frac{\partial }{\partial d}logd(x)p_{data}(x)+\log (1-d(x))p_g(x)\\ =& \frac{1}{d(x)}{p}_{data}(x)-\frac{1}{1-d(x)}{p}_g(x)\end{array}$$
整理得
$$\boxed{d(x)=\frac{p_{data}(x)}{p_g(x)+p_{data}(x)}}$$
$\boxed{将其代入目标函数，并且关于外层g求最小}$
$$\begin{array}{rl}& \underset{g}{\min }{\int }_x\left[\log \frac{p_{data}(x)}{p_g(x)+p_{data}(x)}{p}_{data}(x)+\log (1-\frac{p_{data}(x)}{p_g(x)+p_{data}(x)})p_g(x)\right]dx\\ =& \underset{g}{\min }\left[{\int }_x\log \left(\frac{p_{data}(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\ast \frac{1}{2}\right)p_{data}(x)dx+{\int }_x\log \left(\frac{p_g(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\ast \frac{1}{2}\right)p_g(x)dx\right]\\ =& \underset{g}{\min }\left[{\int }_x\log \left(\frac{p_{data}(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_{data}(x)dx+{\int }_x\log \left(\frac{p_g(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_g(x)dx+\int \log \frac{1}{2}{p}_{data}(x)dx+\int \log \frac{1}{2}{p}_g(x)dx\right]\\ =& \underset{g}{\min }\left[{\int }_x\log \left(\frac{p_{data}(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_{data}(x)dx+{\int }_x\log \left(\frac{p_g(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_g(x)dx+\log \frac{1}{2}\int p_{data}(x)dx+\log \frac{1}{2}\int p_g(x)dx\right]\\ =& \underset{g}{\min }\left[{\int }_x\log \left(\frac{p_{data}(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_{data}(x)dx+{\int }_x\log \left(\frac{p_g(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_g(x)dx+\log \frac{1}{2}+\log \frac{1}{2}\right]\\ =& \underset{g}{\min }\left[{\int }_x\log \left(\frac{p_{data}(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_{data}(x)dx+{\int }_x\log \left(\frac{p_g(x)}{\frac{p_g(x)+p_{data}(x)}{2}}\right)p_g(x)dx+\log \frac{1}{4}\right]\\ =& \underset{g}{\min }kl\left(p_{data}(x)||\frac{p_{data}(x)+p_g(x)}{2}\right)+kl\left(p_g(x)||\frac{p_{data}(x)+p_g(x)}{2}\right)-\log 4\end{array}$$

$kl(p||q)={\int }_{x}p\log \frac{p}{q}dx$，kl散度是衡量概率分布$p$和$q$的相似程度，其大于等于0，当其相似程度一样时，则散度为0，也就是我们要求的最小值。

$\boxed{小补充}$
$$\boxed{2js\left({\mathbf{p}}_{\mathbf{data}}(\mathbf{x})||{\mathbf{p}}_{\mathbf{g}}(\mathbf{x})\right)=\mathbf{kl}\left({\mathbf{p}}_{\mathbf{data}}(\mathbf{x})||\frac{{\mathbf{p}}_{\mathbf{data}}(\mathbf{x})+{\mathbf{p}}_{\mathbf{g}}(\mathbf{x})}{2}\right)+\mathbf{kl}\left({\mathbf{p}}_{\mathbf{g}}(\mathbf{x})||\frac{{\mathbf{p}}_{\mathbf{data}}(\mathbf{x})+{\mathbf{p}}_{\mathbf{g}}(\mathbf{x})}{2}\right)}$$
$js(p||q)$被称为js散度，其仍然是大于等于0的。所以是一样的。

所以
$$p_{data}(x)=\frac{p_g(x)+p_{data}}{2}\to p_{data}=p_g(x)$$
$\boxed{由此可见，目标函数最优值能够让{\mathbb{p}}_g\mathbb{逼近}{\mathbb{p}}_{data}}$，并且当其相等时，有
$$\boxed{d(x)=\frac{p_{data}(x)}{p_g(x)+p_{data}(x)}}=\frac{1}{2}$$
也就是判别器再也无法判断出样本是来自$p_{data}$还是$p_g$

4、代码实现

结果如下

​ 效果一般，在其他变种优化有很多比这个好的，感兴趣的读者自行查阅。

import torch
from torchvision.datasets import mnist
from torchvision import transforms
from torch.utils.data import dataloader
from tqdm  import tqdm
import matplotlib.pyplot as plt

class generate_model(torch.nn.module):
    '''
    生成器
    '''
    def __init__(self):
        super().__init__()
        self.fc=torch.nn.sequential(
            torch.nn.linear(in_features=128,out_features=256),
            torch.nn.tanh(),
            torch.nn.linear(in_features=256,out_features=512),
            torch.nn.relu(),
            torch.nn.linear(in_features=512,out_features=784),
            torch.nn.tanh()
        )
    def forward(self,x):
        x=self.fc(x)
        return x

class distinguish_model(torch.nn.module):
    '''
    判别器
    '''
    def __init__(self):
        super().__init__()
        self.fc=torch.nn.sequential(
            torch.nn.linear(in_features=784,out_features=512),
            torch.nn.tanh(),
            torch.nn.linear(in_features=512,out_features=256),
            torch.nn.tanh(),
            torch.nn.linear(in_features=256,out_features=128),
            torch.nn.tanh(),
            torch.nn.linear(in_features=128,out_features=1),
            torch.nn.sigmoid()
        )
    def forward(self,x):
        x=self.fc(x)
        return x
def train():
    device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu") #判断是否存在可用gpu
    transformer = transforms.compose([
        transforms.totensor(),
        transforms.normalize(mean=0.5, std=0.5)
    ]) #图片标准化
    train_data = mnist("./data", transform=transformer,download=true) #载入图片
    dataloader = dataloader(train_data, batch_size=64,num_workers=4, shuffle=true) #将图片放入数据加载器

    d = distinguish_model().to(device) #实例化判别器
    g = generate_model().to(device) #实例化生成器

    d_optim = torch.optim.adam(d.parameters(), lr=1e-4) #为判别器设置优化器
    g_optim = torch.optim.adam(g.parameters(), lr=1e-4) #为生成器设置优化器

    loss_fn = torch.nn.bceloss() #损失函数

    epochs = 100 #迭代100次
    for epoch in range(epochs):
        dis_loss_all=0 #记录判别器损失损失
        gen_loss_all=0 #记录生成器损失
        loader_len=len(dataloader) #数据加载器长度
        for step,data in tqdm(enumerate(dataloader), desc="第{}轮".format(epoch),total=loader_len):
            # 先计算判别器损失
            sample,label=data #获取样本，舍弃标签
            sample = sample.reshape(-1, 784).to(device) #重塑图片
            sample_shape = sample.shape[0] #获取批次数量
            #从正态分布中抽样
            sample_z = torch.normal(0, 1, size=(sample_shape, 128),device=device)

            dis_true = d(sample) #判别器判别真样本

            true_loss = loss_fn(dis_true, torch.ones_like(dis_true)) #计算损失

            fake_sample = g(sample_z) #生成器通过正态分布抽样生成数据
            dis_fake = d(fake_sample.detach()) #判别器判别伪样本
            fake_loss = loss_fn(dis_fake, torch.zeros_like(dis_fake)) #计算损失

            dis_loss = true_loss + fake_loss #真假加起来
            d_optim.zero_grad()
            dis_loss.backward() #反向传播
            d_optim.step()

            # 生成器损失
            dis_g = d(fake_sample) #判别器判别
            g_loss = loss_fn(dis_g, torch.ones_like(dis_g)) #计算损失
            g_optim.zero_grad()
            g_loss.backward() #反向传播
            g_optim.step()
            with torch.no_grad():
                dis_loss_all+=dis_loss #判别器累加损失
                gen_loss_all+=g_loss #生成器累加损失
        with torch.no_grad():
            dis_loss_all=dis_loss_all/loader_len
            gen_loss_all=gen_loss_all/loader_len
            print("判别器损失为：{}".format(dis_loss_all))
            print("生成器损失为：{}".format(gen_loss_all))
        torch.save(g, "./model/g.pth") #保存模型
        torch.save(d, "./model/d.pth") #保存模型
if __name__ == '__main__':
    # train() #训练模型
    model_g=torch.load("./model/g.pth",map_location=torch.device("cpu")) #载入模型
    fake_z=torch.normal(0,1,size=(10,128))  #抽样数据
    result=model_g(fake_z).reshape(-1,28,28)  #生成数据
    result=result.detach().numpy()

    #绘制
    for i in range(10):
        plt.subplot(2,5,i+1)
        plt.imshow(result[i])
        plt.gray()
    plt.show()

5、结束

以上，就是gan生成对抗网络的全部内容了，如有问题，还望指出。阿里嘎多