n-gram 的局限性
n-gram 只能对于填空这样的通顺性问题做出推测,但是没有办法完全解决句子的语义问题,从而无法实现文本的分类
文本的分类,就是将文本在语义的理解下划分到特定的主题下
手工规则
如一些垃圾过滤系统,需要人工制定规则
准确率往往很高,但是维护规则的成本很大
机器学习
本质上就是学习一个文档到文档类别的映射函数,需要人工分好类的文本作为训练数据,所以是有监督学习
分为学习器和分类器,学习器学习手工标注的数据集并输出训练好的分类器,分类器对于实际需要分类的文档进行分类,选择对应的文档类别进行输出
step1 预处理
依据文本的具体形式来确定:
- 去除 html 标签
- stop-words 停用词:高频的词如冠词,介词往往包含着较少的信息
- word stemming 词干:词的后缀与变形处理,将具有相同词义的词进行合并
step2 文本表示
什么是最好的文本表示方法?
最常用的一种文本表示方法:vsm
vsm(vector space model 向量空间模型)
将文本表示为由词条构成的向量,理论上假设词条之间互相独立,文本可以认为是一种词的集合(词袋)
e.g.在一段文章中按照词频统计出现最多的词,然后进行相关分类
建立文档词条矩阵
a
=
(
a
i
k
)
a=(a_{ik})
a=(aik)
每个文档表示为由词构成的列向量
a
i
k
a_{ik}
aik表示词 k 在文档 i 中的权重
引入符号:
(1)
f
i
k
f_{ik}
fik词条 k 在文档 i 中出现的次数
(2)
n
k
n_{k}
nk词条 k 在文档集合中出现的总次数
(3)n 文档集合包含的文档个数
(4)m 预处理后文档集合包括的词条个数
词的权重
布尔权重:如果词在文档中出现,权重为 1,否则为 0
词条频次权重:使用词条在文档中出现的次数作为权重
逆文档频次:考虑包含某词条的文档个数,
α
∝
1
n
k
\alpha \propto \frac{1}{n_k}
α∝nk1
tf * idf 权重:同时考虑词条频次和逆文档频次,
α
i
k
=
f
i
k
log
(
n
n
k
)
\alpha_{ik} = f_{ik}\log (\frac{n}{n_k})
αik=fiklog(nkn)
tfc 权重:在 tf-idf 基础上对文档长度进行正则化
α
i
k
=
f
i
k
log
(
n
n
k
)
∑
j
=
1
m
[
f
i
j
log
(
n
n
j
)
]
2
\alpha_{ik} = \frac{f_{ik}\log (\frac{n}{n_k})}{\sqrt{\sum\limits_{j=1}^m[f_{ij}\log (\frac{n}{n_j})]^2}}
αik=j=1∑m[fijlog(njn)]2fiklog(nkn)
ltc 权重:将词条频次进行对数化处理,减少绝对频次的巨大差异可能带来的影响
将
f
i
k
f_{ik}
fik和
f
i
j
f_{ij}
fij换成
log
(
f
i
k
+
1
)
\log(f_{ik}+1)
log(fik+1)和
log
(
f
i
j
+
1
)
\log(f_{ij}+1)
log(fij+1)
熵权重:
对于一个词条 k,其信息熵为
1
+
1
log
(
n
)
∑
j
=
1
n
f
j
k
n
k
log
(
f
j
k
n
k
)
1+\frac{1}{\log (n)}\sum\limits_{j=1}^n\frac{f_{jk}}{n_k}\log (\frac{f_{jk}}{n_k})
1+log(n)1j=1∑nnkfjklog(nkfjk)
特殊情况时,如果在所有文档中出现的频数相等,则熵为-1;如果只在一个文档中出现,则熵为 0
熵权重就是在词条的信息熵前乘上对数化词条频次
log
(
f
i
k
+
1
)
∗
(
1
+
1
log
(
n
)
∑
j
=
1
n
f
j
k
n
k
log
(
f
j
k
n
k
)
)
\log(f_{ik}+1)*(1+\frac{1}{\log (n)}\sum\limits_{j=1}^n\frac{f_{jk}}{n_k}\log (\frac{f_{jk}}{n_k}))
log(fik+1)∗(1+log(n)1j=1∑nnkfjklog(nkfjk))
step3 分类模型
最近邻分类器
定义两个样本点之间的距离函数,并将新的样本划分到距离其最近的样本所在的类别中
问题:容易过度拟合数据,比如将错误的数据或者噪声按照定义分类进了对应的组,或是由于其最近邻是噪声而错误分类到了原本不属于新数据的组别
k 近邻分类器
k-nearest neighbour classifier(knn)
为一个新样本点找到最近的 k 个近邻,然后将其划分到这 k 个中所属最多的类别中
训练过程:
给定一个需要训练的实例
x
n
x_n
xn,选出对应 k 个最近实例,返回
y
^
(
x
q
)
←
arg
max
v
∈
v
∑
i
=
1
k
γ
(
v
,
y
(
x
i
)
)
\hat y(x_q) \leftarrow \arg \max\limits_{v\in v}\sum\limits^k_{i=1}\gamma(v,y(x_i))
y^(xq)←argv∈vmaxi=1∑kγ(v,y(xi))
其中 v 为各点对应的集合,
γ
(
a
,
b
)
\gamma(a,b)
γ(a,b)只有在 a=b 时等于 1,else 等于 0
red:k 不可以太高也不可以太低
可以采用验证集来选择合适的 k,距离计算可以采用欧式距离或者余弦距离,采用树结构或者压缩近邻来储存数据
以下是一个较准确的余弦距离说明:
朴素贝叶斯
通过先验事件的知识来预测未来事件
p
(
c
k
∣
x
i
)
=
p
(
x
i
∣
c
k
)
p
(
c
k
)
p
(
x
i
)
p(c_k|x_i)=\frac{p(x_i|c_k)p(c_k)}{p(x_i)}
p(ck∣xi)=p(xi)p(xi∣ck)p(ck)
xi 是 training data,ck 是 hypothesis,那么 p(xi|ck)就是预测可能性
具有条件独立性,即
p
(
x
1
,
x
2
∣
c
)
=
p
(
x
1
∣
c
)
×
p
(
x
2
∣
c
)
p(x_1,x_2|c) = p(x_1|c)\times p(x_2|c)
p(x1,x2∣c)=p(x1∣c)×p(x2∣c)
以邮件分类为例
已有训练数据:训练文章
x
i
x_i
xi,n 种文章种类
c
k
c_k
ck,所有文章中共包括 m 个词,每个词 在第n 个种类下的个数
t
i
j
=
t
11
→
t
n
m
t_{ij} = t_{11} \to t_{nm}
tij=t11→tnm
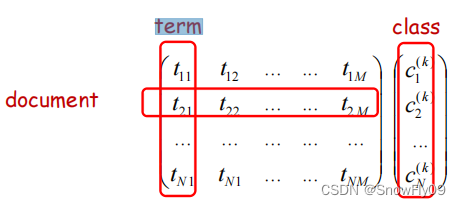
给定一个 email xi,由最大化后验概率:
c
^
=
arg
max
k
(
p
(
c
k
∣
x
i
)
)
=
arg
max
k
(
p
(
c
k
)
p
(
x
i
∣
c
k
)
p
(
x
i
)
)
\hat c=\arg \max_k (p(c_k|x_i))=\arg \max_k (\frac{p(c_k)p(x_i|c_k)}{p(x_i)})
c^=argmaxk(p(ck∣xi))=argmaxk(p(xi)p(ck)p(xi∣ck))
=
arg
max
k
(
p
(
c
k
)
p
(
x
i
∣
c
k
)
)
=
arg
max
k
(
log
p
(
c
k
)
+
log
p
(
x
i
∣
c
k
)
)
=\arg \max_k (p(c_k)p(x_i|c_k))=\arg \max_k(\log p(c_k)+\log p(x_i|c_k))
=argmaxk(p(ck)p(xi∣ck))=argmaxk(logp(ck)+logp(xi∣ck))
=
arg
max
k
(
log
p
(
c
k
)
+
log
∏
j
=
1
m
p
(
t
j
∣
c
k
)
n
i
j
)
=\arg \max_k(\log p(c_k)+\log \prod\limits_{j=1}^m p(t_j|c_k)^{n_{ij}})
=argmaxk(logp(ck)+logj=1∏mp(tj∣ck)nij)
nij 就是词tj 在 email xi 中的个数
根据朴素贝叶斯假设,email类别与词的出现位置无关
已知类别 ck 时 tj 出现的概率

可能存在的问题:数据稀疏&过拟合
使用 laplace 平滑:
p
^
=
n
(
x
i
=
x
i
,
c
=
c
i
)
+
1
n
(
c
=
c
i
)
+
k
\hat p = \frac{n(x_i = x_i,c=c_i)+1}{n(c=c_i)+k}
p^=n(c=ci)+kn(xi=xi,c=ci)+1
step4 评价指标
一般评价
使用训练集进行训练,使用测试集进行测试,在测试集上的准确度来描述模型的准确度
n 倍交叉验证
把数据分成不交叉的五等分,其中一份做测试,另外四份做训练,独立的进行五轮,将这五轮的平均性能作为模型的性能
保留测试
在训练集进行训练,在验证集调整参数,在测试集进行模型评价
混淆矩阵







发表评论