基于最大似然估计(matlab实验)_C/C++

实验内容

1、了解分类和逻辑回归的技术原理，给出满足分类问题的假设函数形式，通过最大似然函数估计推导出新的代价函数
2、针对二分类问题，采用matlab编程，得到分类结果，实验通过程序，分析，加深对逻辑回归分类问题的理解

实验原理

1、分类问题中，由于y是离散值且y∈{0，1}，则假设函数满足0≤h_θ(x)≤1，因此选择：
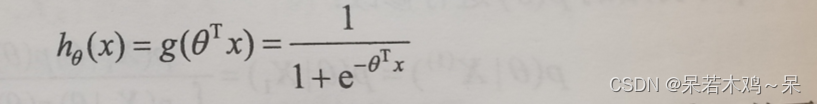
在这里插入图片描述

2、对h_θ(x)输出作进一步解释，h_θ(x)是根据输入x得到的y=1或者(y=0)的可能性。因此假设：
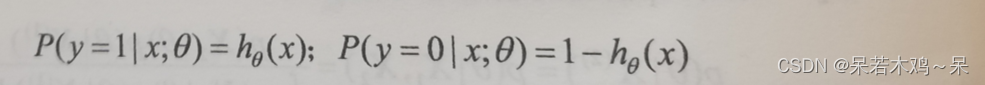
在这里插入图片描述

3、假设m组训练试验是相互独立的，得到似然估计函数：
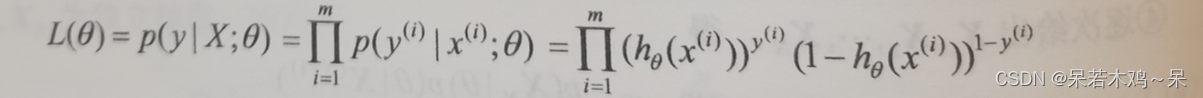
在这里插入图片描述

4、最大似然函数：
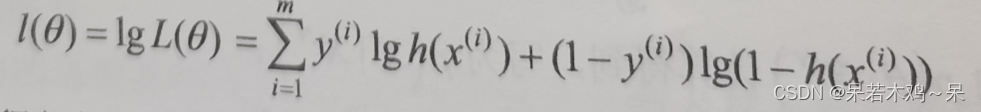
在这里插入图片描述

5、代价函数：
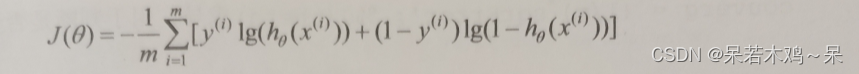
在这里插入图片描述

6、通过批梯度下降，同时更新所有的θ_j：其中α是学习率
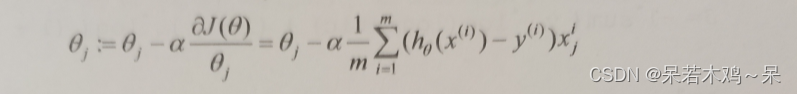
在这里插入图片描述

数据集

链接：https://pan.quark.cn/s/54f8b6d8f1df
提取码：4uws
第一、二列是入学前考试的成绩，第三列为是否可以入学：1(可以)，2(不可以)
在这里插入图片描述

实验过程：

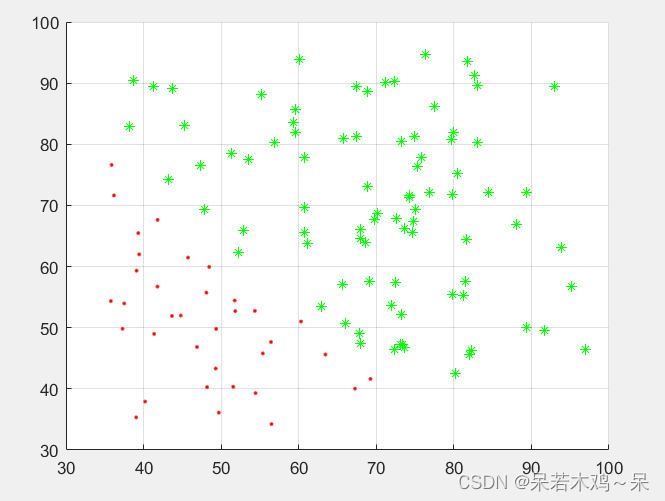
1、划分数据集，并展示训练数据集

>> data = load('e:/桌面/成绩单.txt');
>> x = data(:,1:2);
>> y = data(:,3);
>> [h,w] = size(train_data);
>>  for i=1:h
		if train_data(i,3)==1
			scatter(train_data(i,1),train_data(i,2),'g*');grid on;hold on;
		else
			scatter(train_data(i,1),train_data(i,2),'r.');grid on;hold on;
		end
	end

在这里插入图片描述

2、利用梯度下降算法求解最小的j和theta

%利用梯度下降的算法求解出最小的j和theta
>> alpha = 0.001;%学习率
>> [m,n] = size(x);
>> x = [ones(m,1) x];%特征矩阵
>> initial_theta = zeros(n+1,1);%初始化theta
>> prediction = x*initial_theta;%初始化预测
>> logistic = 1./(1+exp(-prediction));%逻辑函数
>> sqrerror = (logistic-y)'*x;%均方误差
>> theta = initial_theta-alpha*(1/m)*sqrerror';
>> couverg = (1/m)*sqrerror';%j(theta)求导，用于判断是否达到最低点
>> j = -1*sum(y.*log(logistic)+(1-y).*log((1-logistic)))/m;%代价函数
>> a = 1;
>> boolean = zeros(size(x,2),1);
%在最低点处退出循环，即导数为0
%while all(couverg(:)~=boolean(:))
>> while a ~= 40000000
    prediction2 = x*theta;
    logistic1 = 1./(1+exp(-prediction2));
    sqrerror2 = (logistic1-y)'*x;
    j = -1*sum(y.*log(logistic1)+(1-y).*log(1-logistic1))/m;
    theta = theta - alpha*(1/m)*sqrerror2';
    couverg = (1/m)*sqrerror2';
    a = a+1;
    end

解的j：
在这里插入图片描述

解得theta：

在这里插入图片描述

3、预测结果：

%预测某个学生的成绩为[45,90]，求被录取的概率
>> pre1 = logsig([1 45 90]*theta)*100;
>> pre1

pre1 =

    99.93
    
%预测某个学生的成绩为[45,45]，求被录取的概率    
>> pre2 = logsig([1 45 45]*theta)*100;
>> pre2

pre2 =

 	2.73

4、实验总结：
在逻辑分类的代价函数的推导过程中使用了最大似然估计，但最大似然估计求的是最大值，而代价函数求得是最小值，因此只差一个负号，这里的代价函数其实是一个交叉熵。除了梯度下降算法，还可以使用bfgc(变换度法)、l-bfgs(限制变尺度法)，这些算法的优点是可以自动选取好得学习率，通常比下降算法要快的多，但也比较复杂。