Lasso回归系列四：Group Lasso，Sparse Group Lasso_机器学习

lasso变体：group lasso，sparse group lasso

关于lasso回归的讲解可以看我的另一篇博客：lasso回归系列二：lasso回归/岭回归的原理

group lasso

在lasso回归中，是单独地看待每个特征(即假定特征不存在先验的分组)，但有些使用场景下，变量本身就存在分组，比如在股市分析问题中，来自同一个商业领域的公司可以划分到一个小组。在2006年【model selection and estimation in regression with grouped variables】论文提出group lasso，通过引入特征先验的分组信息来解决这类问题：数据的变量之间本身就存在一些已知的分组关系。

根据先验的变量之间的分组信息，权重 $\beta$ 可以被分成 $m$ 组，分组后 $β_g={β(1),β(2),⋯,β(m)}$ ， $β (l)$ 代表一组来自 $β$ 的权重，其中 $ 1≤l≤m$ 。进一步我们对数据 $x$ 也进行分组， $x (i)$ 代表对应 $β (l)$ 的子矩阵。这个优化问题就变成了
$\beta^* = \underset {\beta}{\arg \min} ||y−∑_{l=1}^mx^{(l)}β^{(l)}||^2_2+λ∑_{l=1}^m \sqrt p_l ||β^{(l)}||_2$
其中 $p_l$ 代表 $β^{(l)}$ 中权重参数的个数。

group lasso倾向于把一个组的变量当作一个整体，如果这一组变量是有意义的，那么就会选择该组的所有变量，否则，整组变量对应的参数会被设置为0。

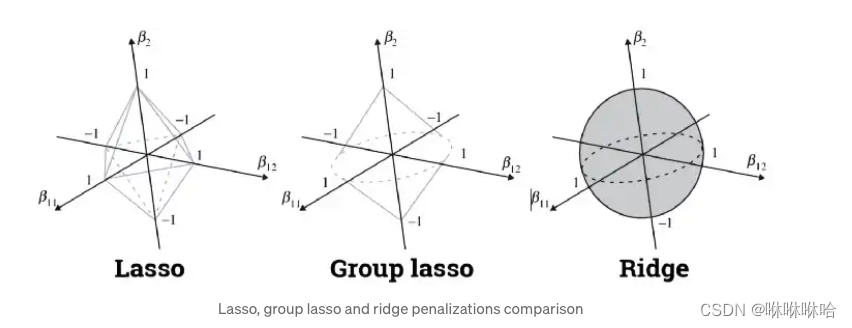
在这里插入图片描述

如上图所示， $\beta_{11}， \beta_{12}$ 是一组变量， $\beta_2$ 是第二组变量，

我们仍旧可以用“不可微分的地方更容易和平方误差等值项相交”的规律来进行分析。在 $<\beta_{11}， \beta_{12}>$ 所在的平面上更容易出现不可微的点，此时 $\beta_2=0$ ，即第二组变量对应 $β$ 的参数为0，第二组变量被抛弃。

此外，我们还可以发现，当m=1时，group lasso就等价于岭回归，当m=n时，group lasso就变成了lasso回归。

sparse group lasso

sparse group lasso是lasso和group lasso的线性结合，最终得到的结果同样也是介于lasso和group lasso的结果之间。

sparse group lasso 是一种非常受欢迎的变量选择方法，能够从最有意义的变量组中选出最有意义的变量。

此时，优化问题就变成了：
$\beta^*= \underset {\beta}{\arg \min} ||y−∑_{l=1}^mx^{(l)}β_{i}||^2_2+\alphaλ∑_{l=1}^n ||β_{i}||_1+(1-\alpha)λ∑_{l=1}^m \sqrt p_l ||β^{(l)}||_2$
其中包含两个需要优化的参数： $\lambda$ 和 $\alpha$ ， $\lambda$ 控制惩罚力度， $\alpha$ 权衡lasso和group lasso的比重，通常可以通过网格搜索确定这两个参数的值。