“物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测;也可以探究不同类之间的相关性和主要差异。聚类和上一讲分类的区别:分类是已知类别的,聚类未知。常用的聚类有基于距离的:包括k-means和系统聚类等,基于密度的dascan算法等。
目录
一、keans和k-means++算法
1.1、k-means算法
我们可以看一下k-means聚类的基本步骤:一、指定需要划分的簇[cù]的个数k值(类的个数);
二、随机地选择k个数据对象作为初始的聚类中心(不一定要是我们的样本点); 三、计算其余的各个数据对象到这k个初始聚类中心的距离,把数据对象划归到距离它最近的那个中心所
处在的簇类中;四、调整新类并且重新计算出新类的中心;五、循环步骤三和四,看中心是否收敛(不变),如果收敛或达到迭代次数则停止循环;六、结束。
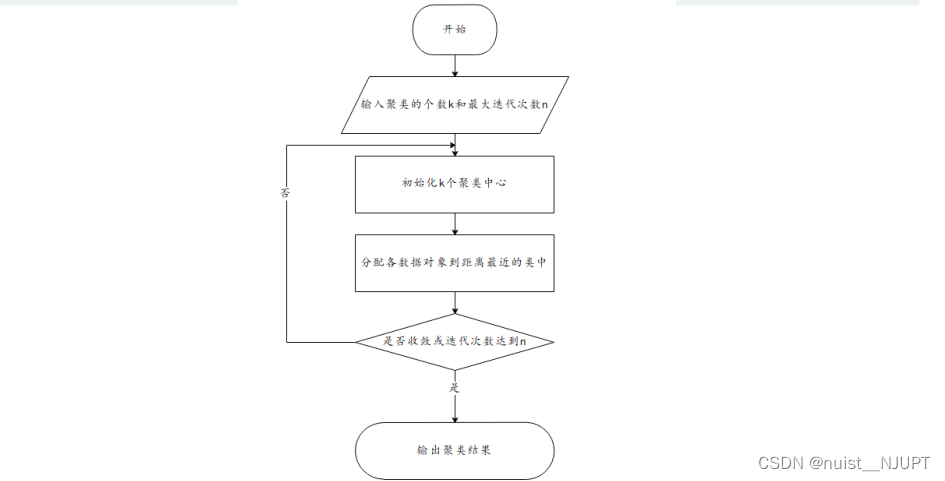
k-means算法由如下优缺点,对于缺点2和缺点3,一般常采用k-means++算法进行改进。
优点:
(1)算法简单、快速。
(2)对处理大数据集,该算法是相对高效率的。
缺点:
(1)要求用户必须事先给出要生成的簇的数目k。
(2)对初值敏感。
(3)对于孤立点数据敏感。
1.2、k-means++算法
k-means++算法选择初始聚类中心的基本原则是:初始的聚类中心之间的相互距离要尽可能的远。
算法描述如下:只对k-means算法“初始化k个聚类中心” 这一步进行了优化)
步骤一:随机选取一个样本作为第一个聚类中心;
步骤二:计算每个样本与当前已有聚类中心的最短距离(即与最近一个聚类中心的距离),这个值越大,表示被选取作为聚类中心的概率较大;最后,用轮盘法(依据概率大小来进行抽选)选出下一个聚类中心;
步骤三:重复步骤二,直到选出k个聚类中心。选出初始点后,就继续使用标准的k-means算法了。
下面演示使用spss完成聚类操作,spss默认使用的是k-means++算法实现的,这里面我选择的k是3,即聚类成3个,可以描述成发达城市,中部城市和不发达城市。
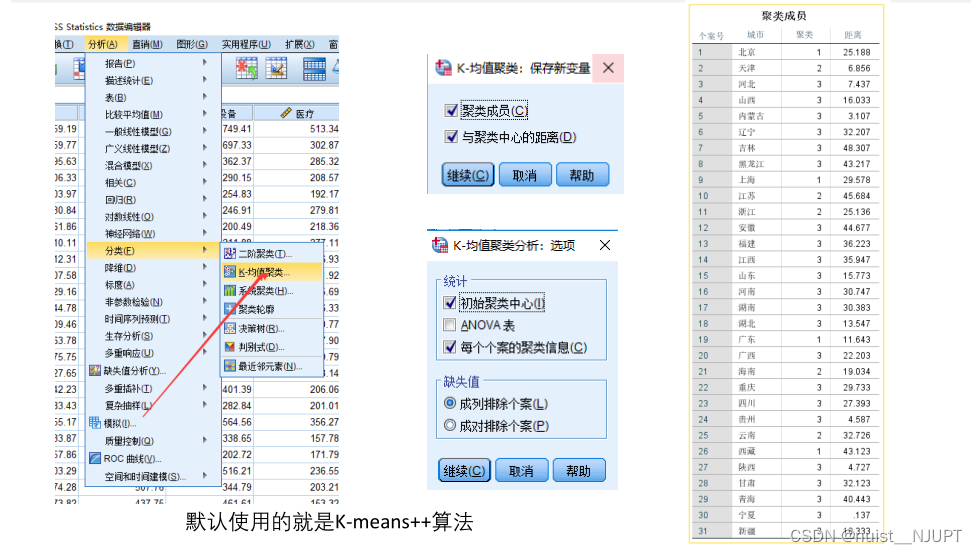
使用spss进行k-means++聚类,虽然可以很好地选择聚类中心,但是对于聚类中心的个数k的问题,还是需要主观堆的经验判断,所以还是有缺点的。如果出现数据量纲不同,应该先进行数据规范化处理,再进行聚类,spss勾选将标准值另存为变量,即可实现数据的标准化处理。
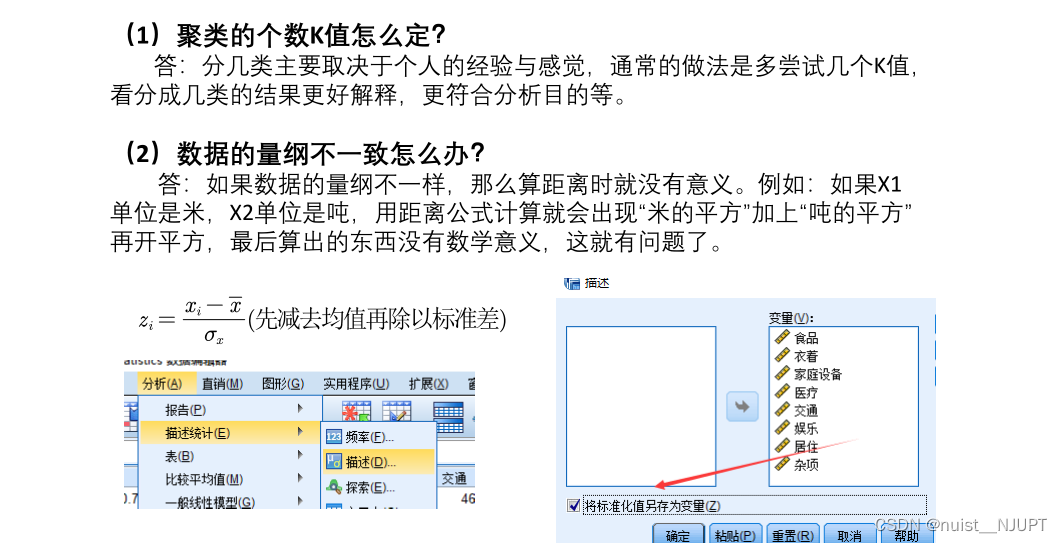
二、系统(层次)聚类
2.1、系统聚类基本原理
系统聚类的过程不需要提前设置聚类个数和初始聚类点,系统聚类的流程如下:
系统(层次)聚类的算法流程:
一、将每个对象看作一类,计算两两之间的最小距离;
二、将距离最小的两个类合并成一个新类;
三、重新计算新类与所有类之间的距离;
四、重复二三两步,直到所有类最后合并成一类;
五、画聚类图决定分类个数和类别。
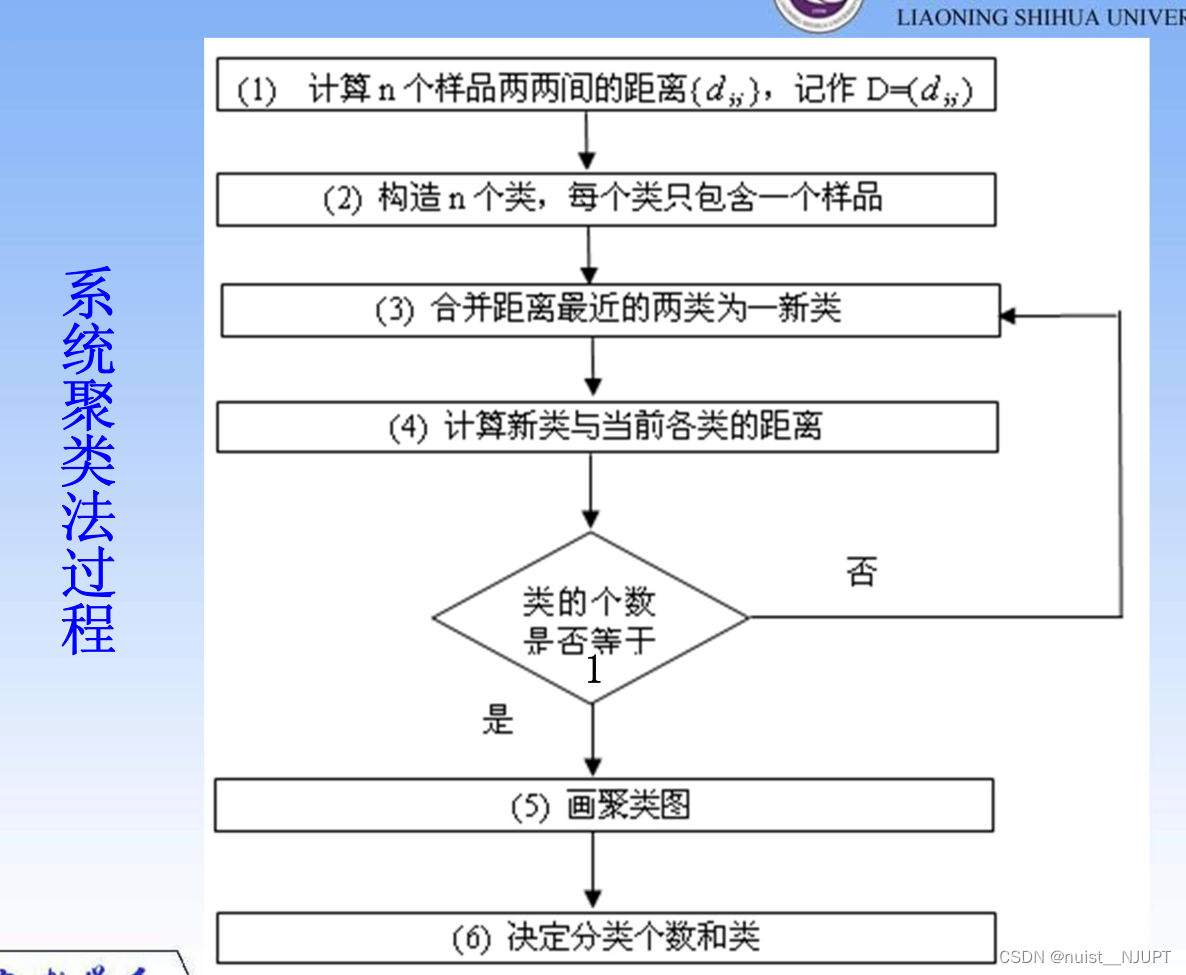
对于需要计算的距离,对于样本与样本之间的距离,常用的距离公式如下:

对于指标和指标之间的距离,常用的距离计算公式如下:

另外,类与类之间的距离常用的计算方式有如下几种:
1)最短距离法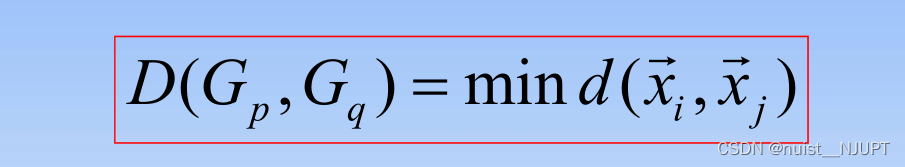
2)最长距离法
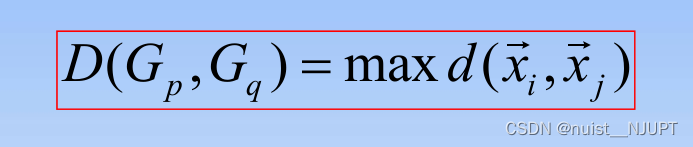
3)组间/组内平均连接法
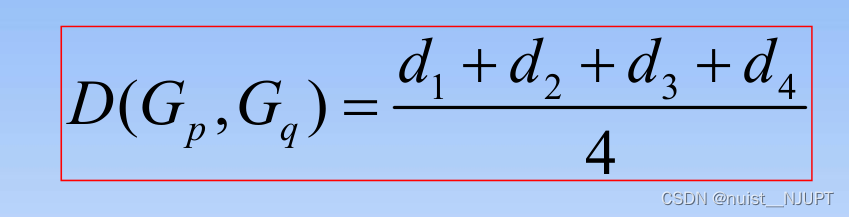 4)重心法
4)重心法
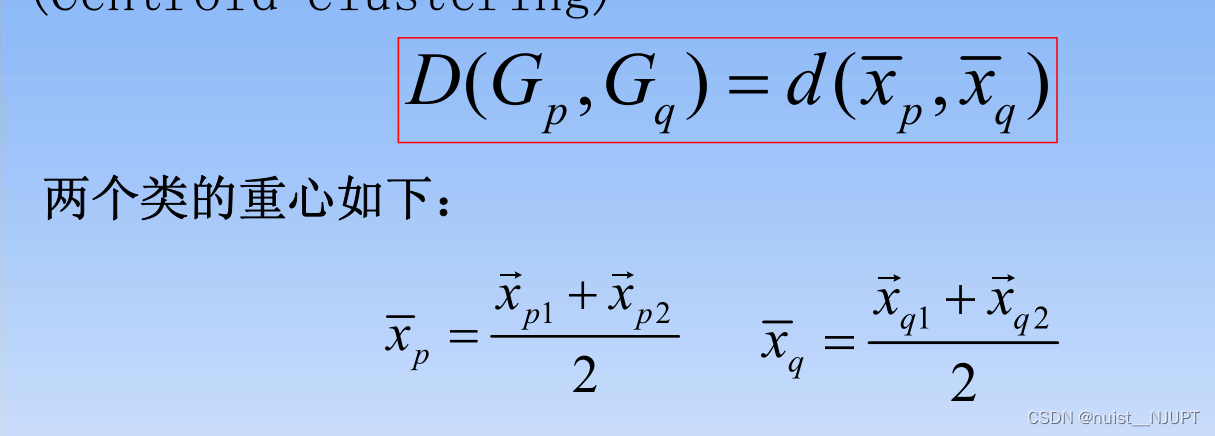
2.2、系统聚类spss实现
在spss中选择系统聚类,导入变量,如果量纲不同,可以消除, 可以设置绘制谱系图等。
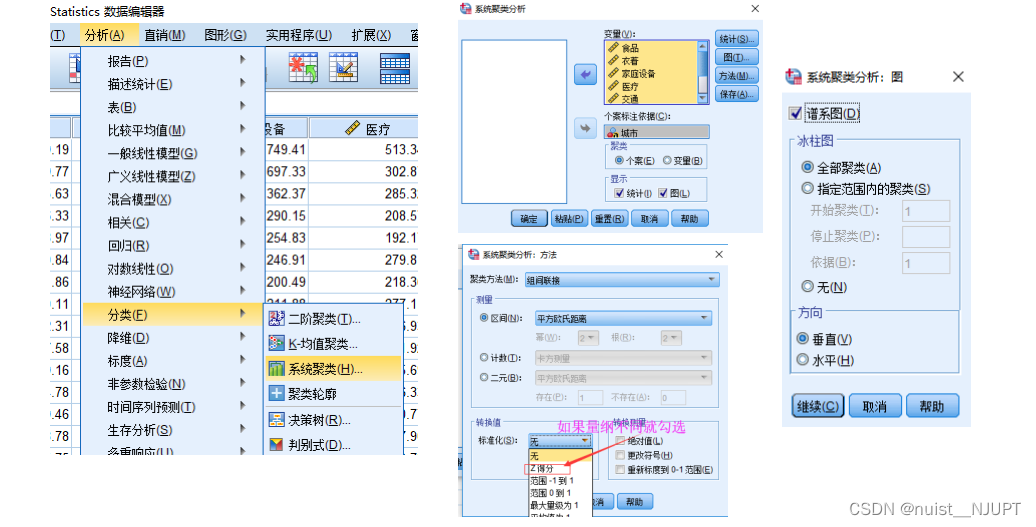
谱系图如下所示,图中的红线是我画上去的,通过红线可以确定分类的个数,主要根据可解释性划分类别,该图中横轴表示各类之间的距离。
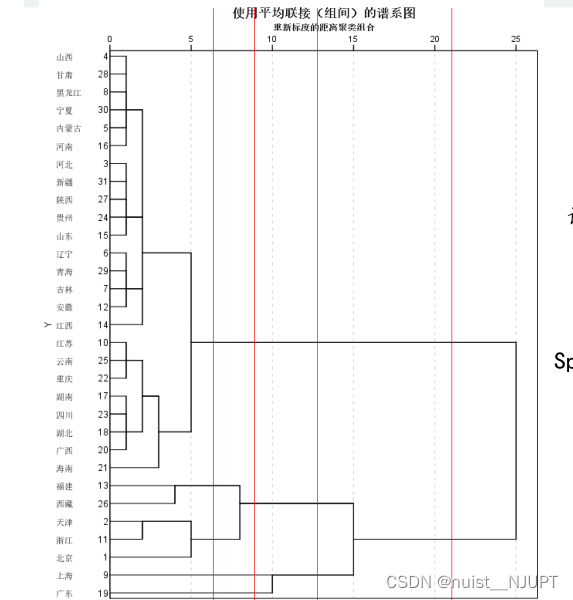
另外除了在图中画竖线确定k的个数,另外有一种常见的方法用来确定聚类数k的值,就是肘部法,具体如下:

我们通过spss进行系统聚类,会生成聚合系数,我们将聚合系数由大到小降序排列后绘图,找到类似肘部的点,即为聚类类别数k。
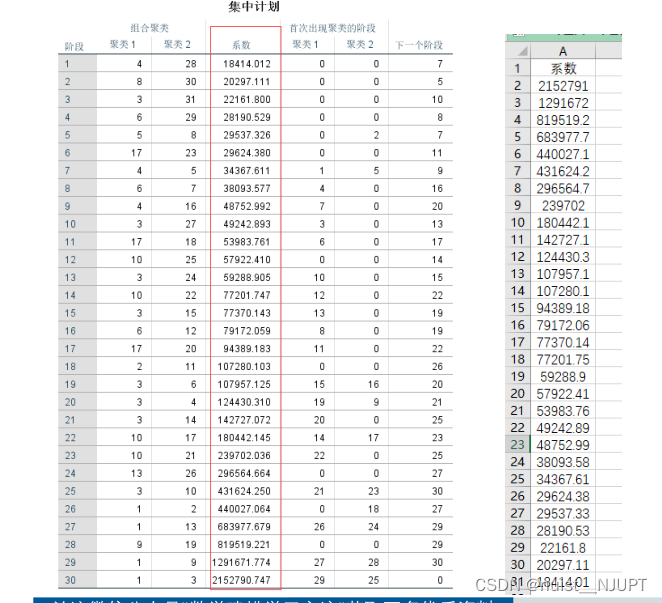
我们可以看到绘制的图形中可以去k=3或者k=5,是最好的类别,至于具体取哪个,结合具体的解释性,哪个解释性强,取哪个。
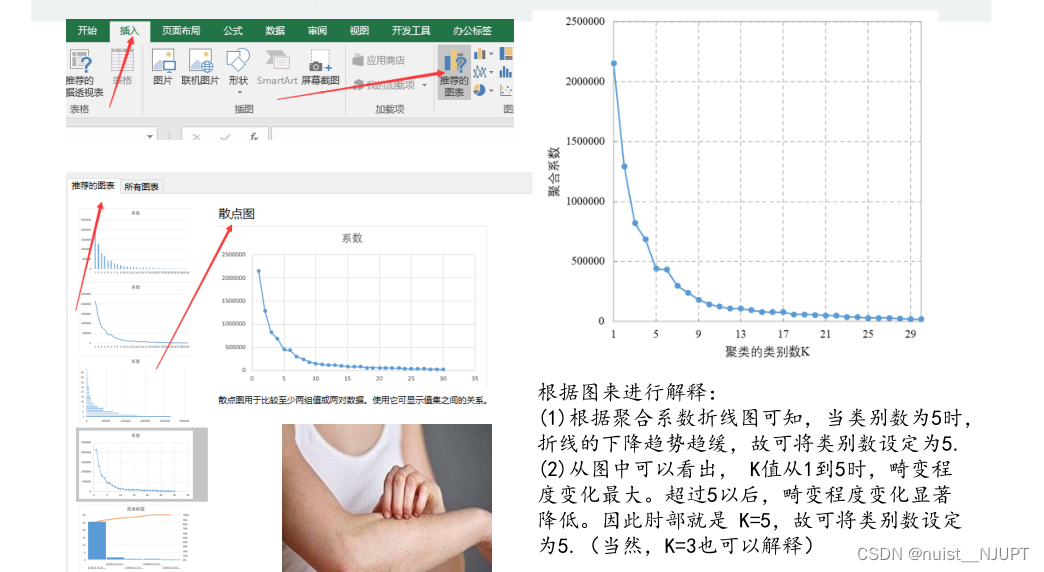
确定聚类个数k后,可以保存聚类结果并绘图,具体如下,当然只能绘制2维或者3维图,即只有当有2个或者三个变量进行聚类才能绘制出图形。
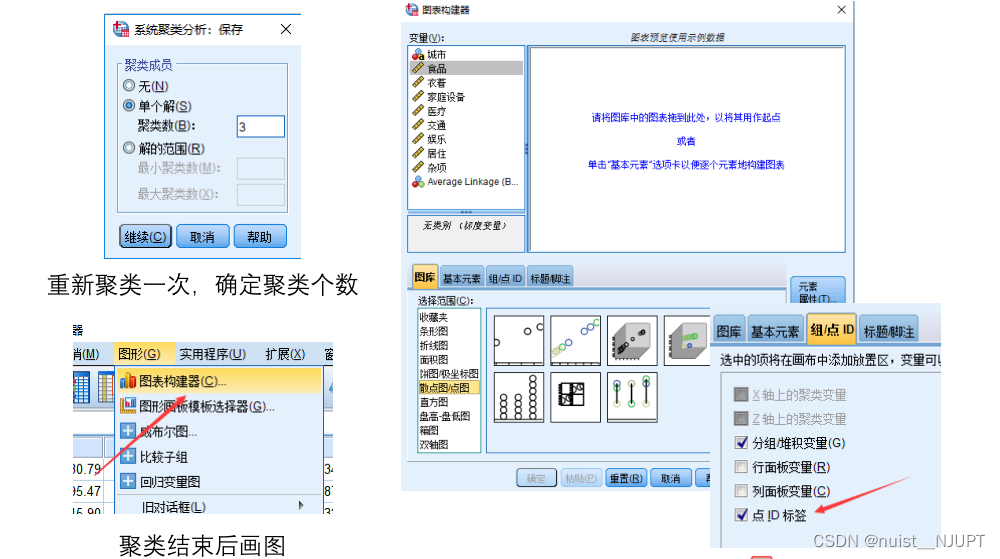
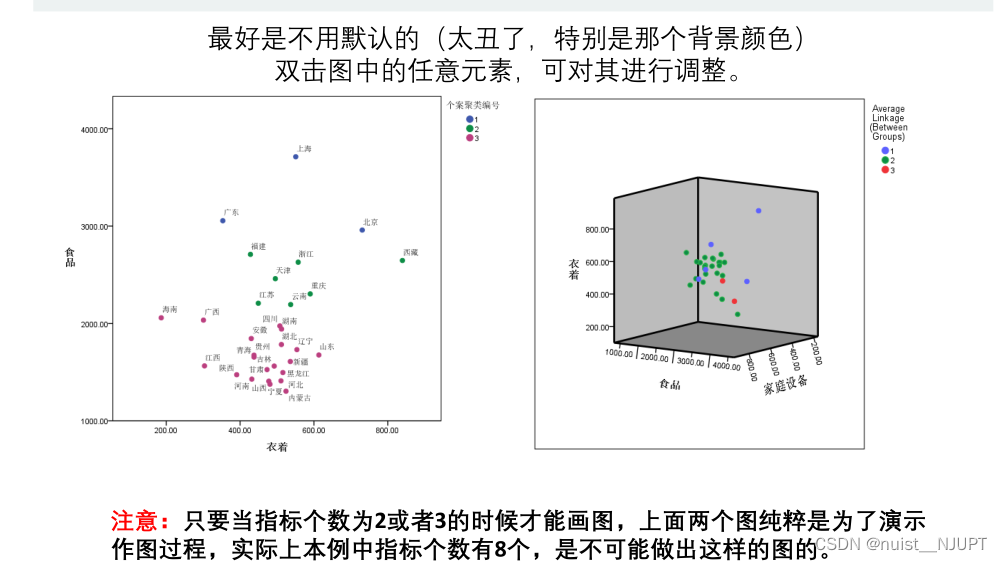
最后绘制的二维和三维图形如下所示:
三、dbscan算法
3.1、dbscan算法基本原理
dbscan算法是具有噪声的基于密度的聚类方法,根据挨的近按一定的数量进行聚类。

dbscan算法的数据分类如下:主要分成三类,即核心点,边界点,噪声点。
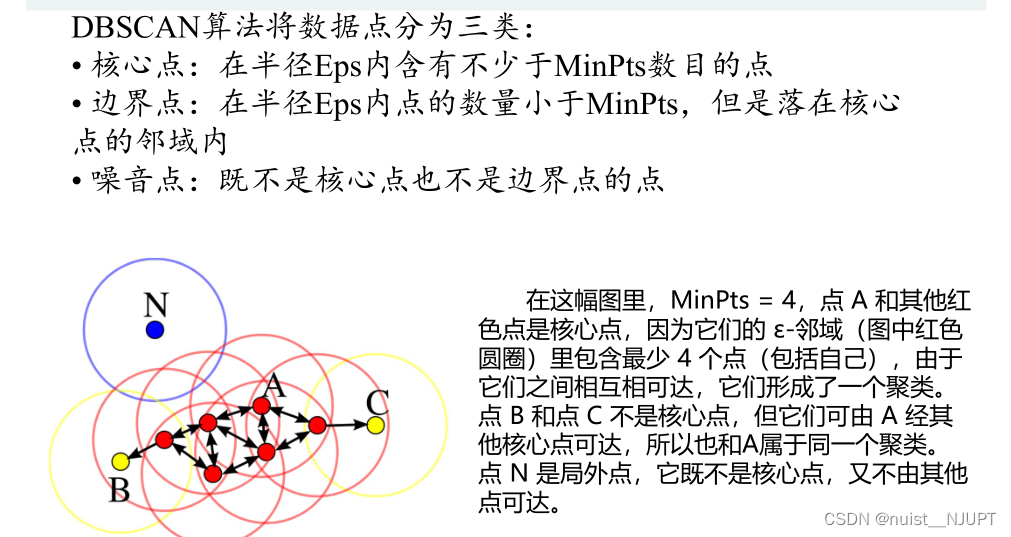
dbscan算法的优缺点如下:其实除非指标绘制的散点图有明显的特殊形状,可以考虑使用dbscan算法,一般还是用系统聚类比较好。

3.2、dbscan算法matlab实现
主函数如下,脚本主程序如下:
clc;
clear;
close all;
%% load data
load smile;
x = smile;
%% run dbscan clustering algorithm
epsilon=0.5;
minpts=10;
idx=dbscan(x,epsilon,minpts);
%% plot results
%如果只要两个指标的话就可以画图啦
plotclusterinresult(x, idx);
title(['dbscan clustering (\epsilon = ' num2str(epsilon) ', minpts = ' num2str(minpts) ')']);dbscan算法实现的函数如下:
function [idx, isnoise]=dbscan(x,epsilon,minpts)
c=0;
n=size(x,1);
idx=zeros(n,1); % 初始化全部为0,即全部为噪音点
d=pdist2(x,x);
visited=false(n,1);
isnoise=false(n,1);
for i=1:n
if ~visited(i)
visited(i)=true;
neighbors=regionquery(i);
if numel(neighbors)<minpts
% x(i,:) is noise
isnoise(i)=true;
else
c=c+1;
expandcluster(i,neighbors,c);
end
end
end
function expandcluster(i,neighbors,c)
idx(i)=c;
k = 1;
while true
j = neighbors(k);
if ~visited(j)
visited(j)=true;
neighbors2=regionquery(j);
if numel(neighbors2)>=minpts
neighbors=[neighbors neighbors2]; %#ok
end
end
if idx(j)==0
idx(j)=c;
end
k = k + 1;
if k > numel(neighbors)
break;
end
end
end
function neighbors=regionquery(i)
neighbors=find(d(i,:)<=epsilon);
end
end绘图的matlab代码如下:
function plotclusterinresult(x, idx)
k=max(idx);
colors=hsv(k);
legends = {};
for i=0:k
xi=x(idx==i,:);
if i~=0
style = 'x';
markersize = 8;
color = colors(i,:);
legends{end+1} = ['cluster #' num2str(i)];
else
style = 'o';
markersize = 6;
color = [0 0 0];
if ~isempty(xi)
legends{end+1} = 'noise';
end
end
if ~isempty(xi)
plot(xi(:,1),xi(:,2),style,'markersize',markersize,'color',color);
end
hold on;
end
hold off;
axis equal;
grid on;
legend(legends);
legend('location', 'northeastoutside');
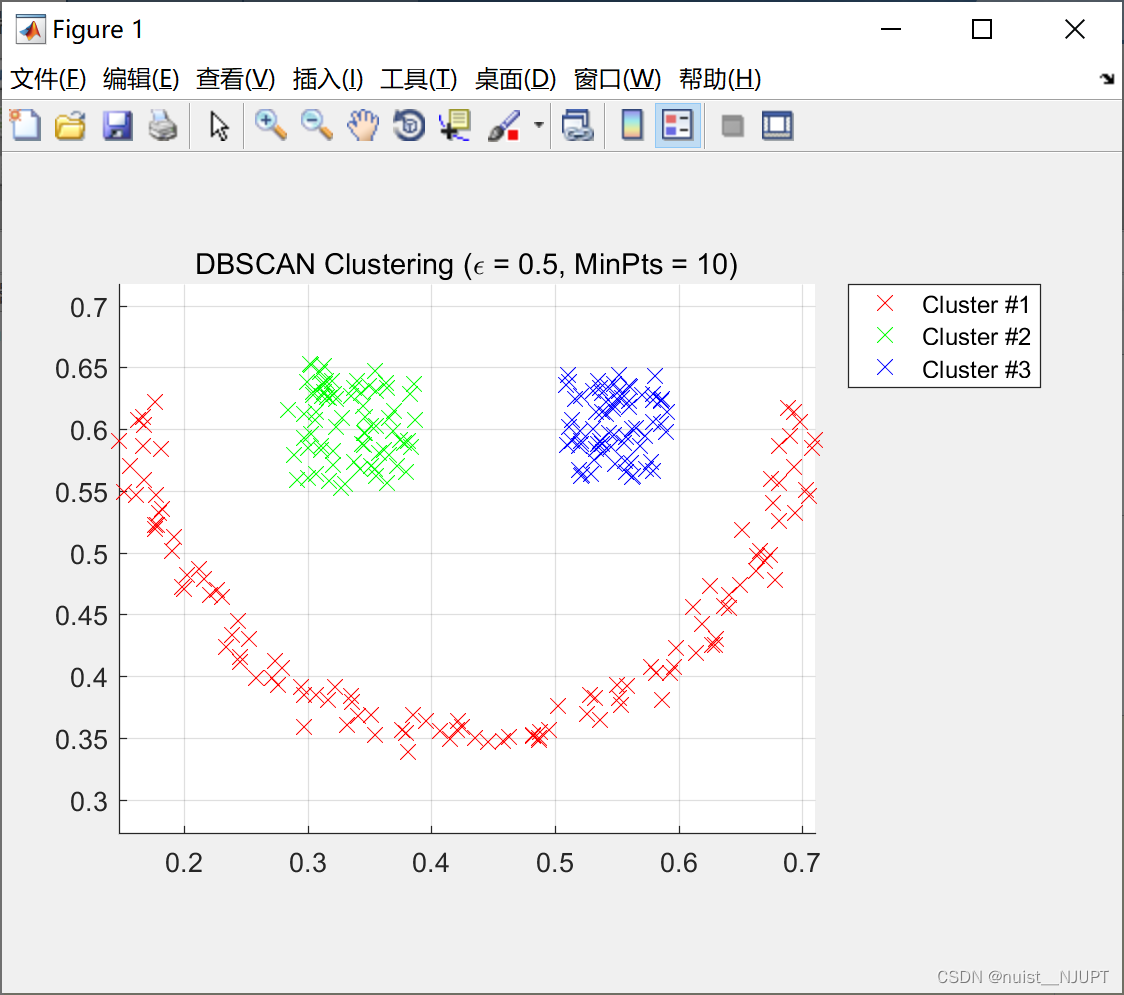
end我们可以看到使用的smile数据集,最后聚类成3个部分,刚好是一个 微笑的表情。




发表评论