k-means聚类算法
- k-means聚类算法在1967年由j.b.macqueen提出,是一种基于划分的动态聚类算法,同时也是一种具有较大影响力的无监督学习算法。该算法是对一个n维向量的数据点集d={xi|i=1,···,n}进行聚类,其中xi表示第i个数据点,最终将集合d划分成k个类簇。分组的依据主要把越相似、差异越小的样本聚成一类(簇),最后形成多个簇,使同一个簇内部的样本相似度高,不同簇之间差异性高。
距离的度量有欧几里得距离、曼哈顿距离和切比雪夫距离,如下所示:
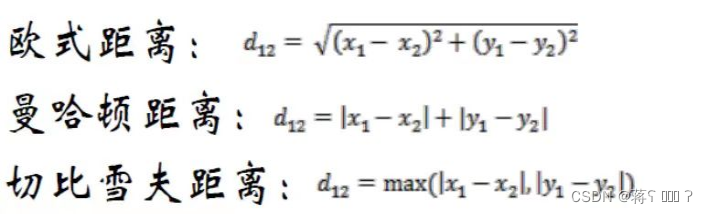
检验聚类结果的方法:
- 肘部法sse(sum of the squared errors,误差平方和),利用计算误方差和,来实现对不同k值的选取后,每个k值对应簇内的点到中心点的距离误差平方和,理论上sse的值越小,代表聚类效果越好,通过数据测试,sse的值会逐渐趋向一个最小值。
误差平方和sse计算公式 sse=![]()
式中:ci为第i个类簇;c i为簇c i的聚类中心;x为 数据集d中的数据对象;k为类簇数目。
- 轮廓系数(silhouette coefficient),是聚类效果好坏的一种评价方式。最早由 peter j. rousseeuw 在 1986 提出。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。
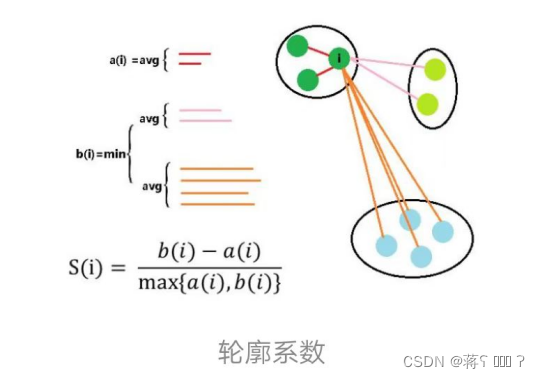
a(i) :i向量到同一簇内其他点不相似程度的平均值
b(i) :i向量到其他簇的平均不相似程度的最小值
可见轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优。
- 选择k个数据作初始聚类中心
- 分别计算所有数据点到各个初始聚类中心的距离,
- 将数据点就近分配到各个初始聚类中心所在的集合中形成一个簇。
- 根据簇中的各个点,更新每个簇的中心。(计算中心样本均值作为新的中心)
- 重复分配和更新的步骤,直到簇基本不再发生变化时,算法结束。
具体步骤程如图所示: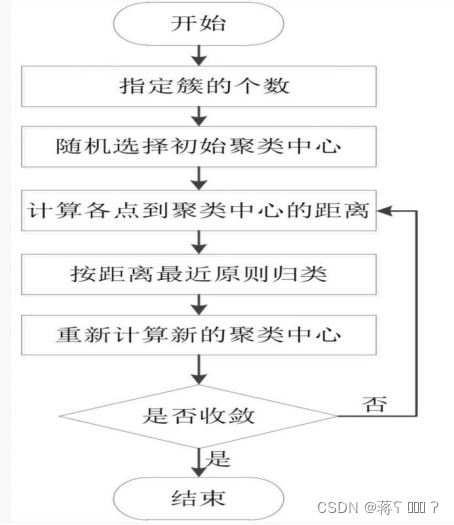
- 原理比较简单,实现也是很容易,收敛速度快。
- 当结果簇是密集的,而簇与簇之间区别明显时, 它的效果较好。
- 主要需要调参的参数仅仅是簇数k。
- k值需要预先给定,很多情况下k值的估计是非常困难的。
- k-means算法对初始选取的中心点是敏感的,不同的随机种子点得到的聚类结果完全不同 ,对结果影响很大。
- 对于噪音和异常点比较敏感。
- 结果不一定是全局最优,只能保证局部最优。
3、matlab代码运行结果
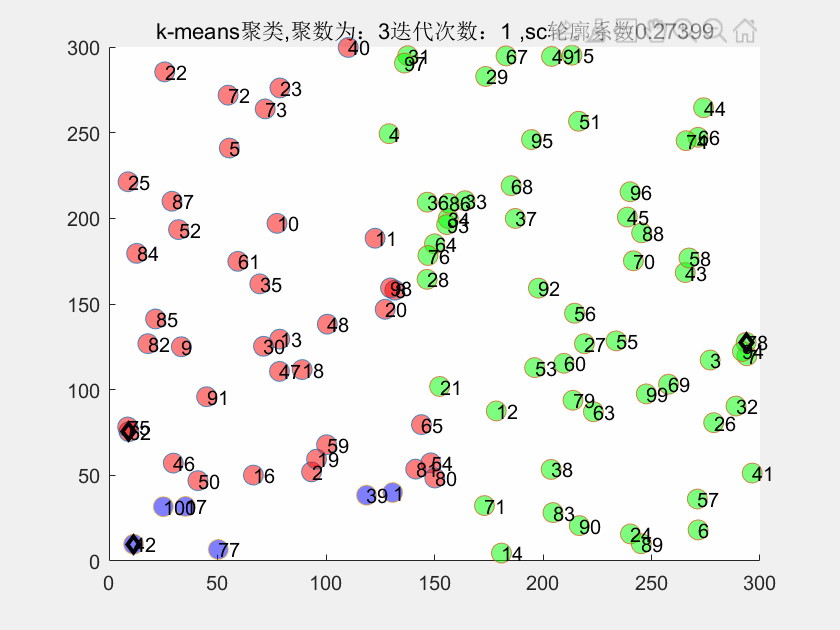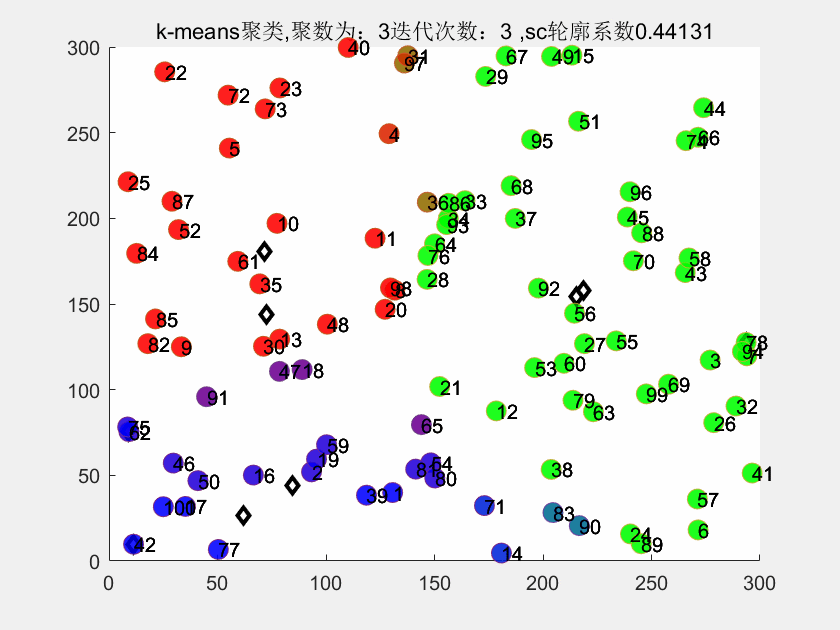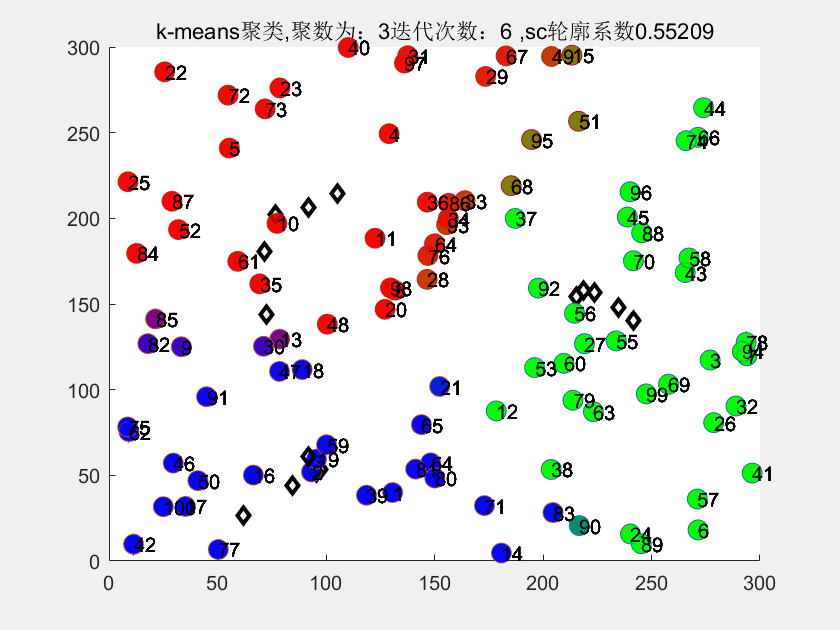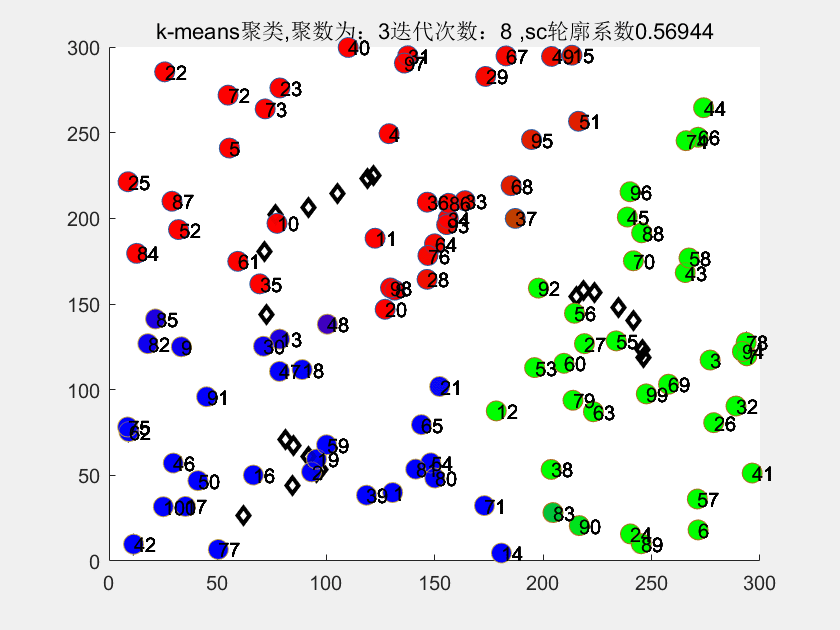
4、部分代码
clc;
clear all;
close all;
data(:,1)=rand(1,100)*300;%data的第一列在1-300间取100个数
data(:,2)=rand(1,100)*300;%data的第二列在1-300间取100个数
%% 用原理推导k-means算法
[m,n]=size(data);%判断data的行数m和列数n
k=3;%聚类数
center=data(randperm(m,k),:);%随机选择m行中的k个做为初始中心
maxgen=50;%最大迭代次数
lim=0.001;%中心变化阈值,当新产生的中心与前一个中心小于这个阈值时结束聚类
for i=1:maxgen
for j=1:k
distance=(data-repmat(center(j,:),m,1)).^2;%计算每个样本到选取中心的距离
distance1(:,j)=sqrt(sum(distance'));%欧式距离
end
[~,indexk]=min(distance1');%找出每一行最小的所在的位置
%新的中心位置分类后各样本均值
for g=1:k
newcenter(g,:)=mean(data(find(indexk==g),:));
end
%% 作图
a=unique(indexk);%找出分类出的个数即k的值1 2 3
c=cell(1,length(a));%加入元胞数组,1行a的长度为列
%将同一数值的加入到同一元素内
for t=1:length(a)
c(1,t)={find(indexk==a(t))};
end
%对分好类的数据根据其范围填充相应颜色
for j=1:k
getdata=data(c{1,j},:);
if j==1
%大小100,颜色填充红/绿/蓝/黄/青,里面透明度0.5,边缘透明度0.7
scatter(getdata(:,1),getdata(:,2),100,"markerfacecolor",[1 0 0],"markerfacealpha",0.5,"markeredgealpha",0.7);
else if j==2
scatter(getdata(:,1),getdata(:,2),100,"markerfacecolor",[0 1 0],"markerfacealpha",0.5,"markeredgealpha",0.7);
else if j==3
scatter(getdata(:,1),getdata(:,2),100,"markerfacecolor",[0 0 1],"markerfacealpha",0.5,"markeredgealpha",0.7);
else if j==4
scatter(getdata(:,1),getdata(:,2),100,"markerfacecolor",[1 1 0],"markerfacealpha",0.5,"markeredgealpha",0.7);
else
scatter(getdata(:,1),getdata(:,2),100,"markerfacecolor",[0 1 1],"markerfacealpha",0.5,"markeredgealpha",0.7);
end
end
end
end
hold on
end
%给每个位置加上序号
for f=1:max(size(data))
h=num2str(f);
text(data(f,1),data(f,2),h);
end
%中心点用黑色菱形表示
plot(center(:,1),center(:,2),"kd","linewidth",2)
%评价聚类好坏的指标
sc=mean(silhouette(data,indexk'));
title(['k-means聚类,聚数为:',num2str(k),'迭代次数:',num2str(i),' ,sc轮廓系数',num2str(sc)])
%% 判断新的中心和原来的中心是否基本不变,小于阈值则算法结束,否则继续
if (sqrt(sum((newcenter-center).^2))>lim)
center=newcenter;
else
break;
end
end
center原输入值取得随机数,每次所得结果不尽相同,可自行更换为需要的数据。
完整源码获得方式:微信或qq联系

发表评论