Scikit-Learn 1.4使用指南：无监督学习 双聚类 Biclustering

例如，给定一个形状为(10, 10)的矩阵，一个可能的双聚类具有三行和两列，它诱导出一个形状为(3, 2)的子矩阵：

import numpy as np
data = np.arange(100).reshape(10, 10)
rows = np.array([0, 2, 3])[:, np.newaxis]
columns = np.array([1, 2])
data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

为了可视化，给定一个双聚类，可以重新排列数据矩阵的行和列，使得双聚类连续。

算法在定义双聚类的方式上有所不同。一些常见的类型包括：

• 常数值、常数行或常数列
• 异常高或低的值
• 方差较低的子矩阵
• 相关的行或列

算法在如何将行和列分配给双聚类上也有所不同，这导致了不同的双聚类结构。当行和列被划分为分区时，会出现块对角线或棋盘格结构。

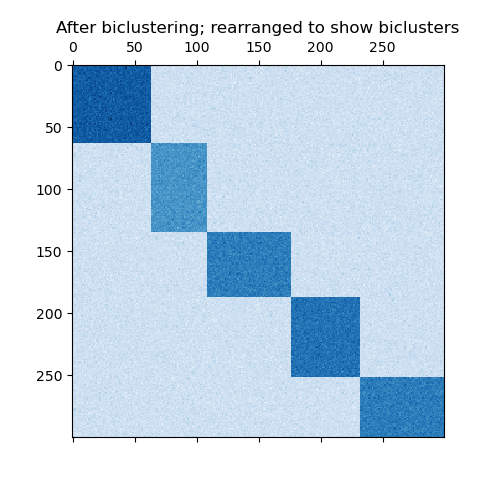
如果每行和每列都属于一个双聚类，那么重新排列数据矩阵的行和列将在对角线上显示双聚类。下面是一个具有此结构的示例，其中双聚类的平均值高于其他行和列：

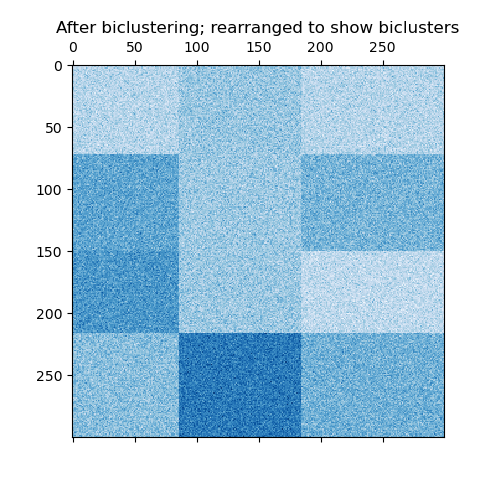
棋盘格情况下，每行属于所有列聚类，每列属于所有行聚类。下面是一个具有此结构的示例，其中每个双聚类内的值的方差很小：

在拟合模型后，可以在rows_和columns_属性中找到行和列的聚类成员关系。rows_[i]是一个二进制向量，非零条目对应于属于双聚类i的行。类似地，columns_[i]指示属于双聚类i的列。

一些模型还具有row_labels_和column_labels_属性。这些模型将行和列分区，例如块对角线和棋盘格双聚类结构。

sklearn.cluster

谱共聚类

spectralcoclustering算法找到具有高于其他行和列对应值的双聚类。每行和每列都属于一个双聚类，因此重新排列行和列以使分区连续会显示这些高值沿对角线：

数学公式

通过图的拉普拉斯矩阵的广义特征值分解，可以找到最优归一化割的近似解。通常，这意味着直接使用拉普拉斯矩阵进行计算。如果原始数据矩阵$a$的形状为$m\times n$，则对应二分图的拉普拉斯矩阵的形状为$(m+n)\times (m+n)$。然而，在这种情况下，可以直接使用较小且更高效的$a$进行计算。

输入矩阵$a$的预处理如下：

$$a_n=r^{-1/2}a{c}^{-1/2}$$

其中$r$是对角矩阵，其第$i$个条目等于${\sum }_j{a}_{ij}$，$c$是对角矩阵，其第$j$个条目等于${\sum }_i{a}_{ij}$。

奇异值分解$a_n=u\sigma v^{\top }$提供了$a$的行和列的分区。左奇异向量的子集给出了行分区，右奇异向量的子集给出了列分区。

从第二个开始的$\ell =\lceil {\log }_{2}k\rceil$个奇异向量提供了所需的分区信息。它们用于形成矩阵$z$：

z = [ r − 1 / 2 u c − 1 / 2 v ] \begin{aligned} z = \begin{bmatrix} r^{-1/2} u \\\\ c^{-1/2} v \end{bmatrix} \end{aligned} z= ​r−1/2uc−1/2v​ ​​

其中$u$的列为$u_2,\dots ,u_{\ell +1}$，$v$的列也是如此。

然后，使用k-means对$z$的行进行聚类。前n_rows个标签提供行分区，剩余的n_columns个标签提供列分区。

示例：

• sphx_glr_auto_examples_bicluster_plot_spectral_coclustering.py：一个简单的示例，展示如何生成一个具有双聚类的数据矩阵，并对其应用此方法。
• sphx_glr_auto_examples_bicluster_plot_bicluster_newsgroups.py：在twenty newsgroup数据集中查找双聚类的示例。

参考文献：

• dhillon, inderjit s, 2001. co-clustering documents and words using bipartite spectral graph partitioning <10.1145/502512.502550>

谱双聚类

spectralbiclustering算法假设输入数据矩阵具有隐藏的棋盘格结构。具有此结构的矩阵的行和列可以被分区，以使得行聚类和列聚类的笛卡尔积中的任何双聚类的条目近似恒定。例如，如果有两个行分区和三个列分区，每行将属于三个双聚类，每列将属于两个双聚类。

该算法将矩阵的行和列分区，以便相应的分块常数棋盘格矩阵提供对原始矩阵的良好近似。

数学公式

首先，将输入矩阵$a$归一化，以使棋盘格模式更明显。有三种可能的方法：

1. 独立的行和列归一化，与谱共聚类中的方法相同。该方法使得行之和为一个常数，列之和为另一个常数。
2. 双随机化：重复的行和列归一化，直到收敛。该方法使得行和列之和都为相同的常数。
3. 对数归一化：计算数据矩阵的对数：$l=\log a$。然后计算$l$的列均值$\overline{l_{i\cdot }}$，行均值$\overline{l_{\cdot j}}$和总体均值$\overline{l_{\cdot \cdot }}$。根据以下公式计算最终矩阵：

$$k_{ij}=l_{ij}-\overline{l_{i\cdot }}-\overline{l_{\cdot j}}+\overline{l_{\cdot \cdot }}$$

归一化后，计算前几个奇异向量，就像谱共聚类算法一样。

如果使用了对数归一化，所有奇异向量都是有意义的。然而，如果使用了独立归一化或双随机化，将丢弃第一个奇异向量$u_1$和$v_1$。从现在开始，“第一个”奇异向量指的是$u_2\dots u_{p+1}$和$v_2\dots v_{p+1}$，除非是对数归一化的情况。

给定这些奇异向量，根据哪些可以最好地由分段常数向量逼近，对这些奇异向量进行排序。使用一维k-means找到每个向量的逼近，并使用欧氏距离对其进行评分。选择最佳左奇异向量和右奇异向量的某个子集。接下来，将数据投影到这些最佳奇异向量的子集上并进行聚类。
示例：

• sphx_glr_auto_examples_bicluster_plot_spectral_biclustering.py：一个简单的示例，展示了如何生成一个棋盘状的矩阵并对其进行双聚类。

参考文献：

• kluger, yuval, et. al., 2003. spectral biclustering of microarray data: coclustering genes and conditions <10.1101/gr.648603>

sklearn.metrics

双聚类评估

对于双聚类结果的评估有两种方式：内部评估和外部评估。内部评估，如聚类稳定性，仅依赖于数据和结果本身。目前 scikit-learn 中没有内部双聚类评估指标。外部评估则是指与外部信息源（如真实解）进行比较。在处理真实数据时，真实解通常是未知的，但对人工数据进行双聚类可能有助于准确评估算法，因为真实解是已知的。

要将一组找到的双聚类与真实双聚类进行比较，需要两个相似度度量：用于单个双聚类的相似度度量，以及将这些单个相似度组合成一个总体分数的方法。

为了比较单个双聚类，已经使用了几种度量方法。目前，只实现了 jaccard 系数：

$$j(a,b)=\frac{|a\cap b|}{|a|+|b|-|a\cap b|}$$

其中 $a$ 和 $b$ 是双聚类，$|a\cap b|$ 是它们交集中的元素数量。当双聚类完全不重叠时，jaccard 系数的最小值为 0，当它们完全相同时，最大值为 1。

已经开发了几种方法来比较两组双聚类。目前，只有 consensus_score (hochreiter et. al., 2010) 可用：

1. 使用 jaccard 系数或类似的度量方法，对一对双聚类（分别来自两组）计算双聚类的相似度。
2. 以一对一的方式将一组双聚类分配给另一组，以最大化它们的相似度之和。这一步使用匈牙利算法来执行。
3. 最终的相似度之和除以较大集合的大小。

最小的一致性分数 0 发生在所有双聚类对完全不相似的情况下。最大分数 1 发生在两组双聚类完全相同的情况下。

参考文献：

• hochreiter, bodenhofer, et. al., 2010. fabia: factor analysis for bicluster acquisition。