【算法/训练】：动态规划（线性DP）_算法

一、路径类

1. 字母收集

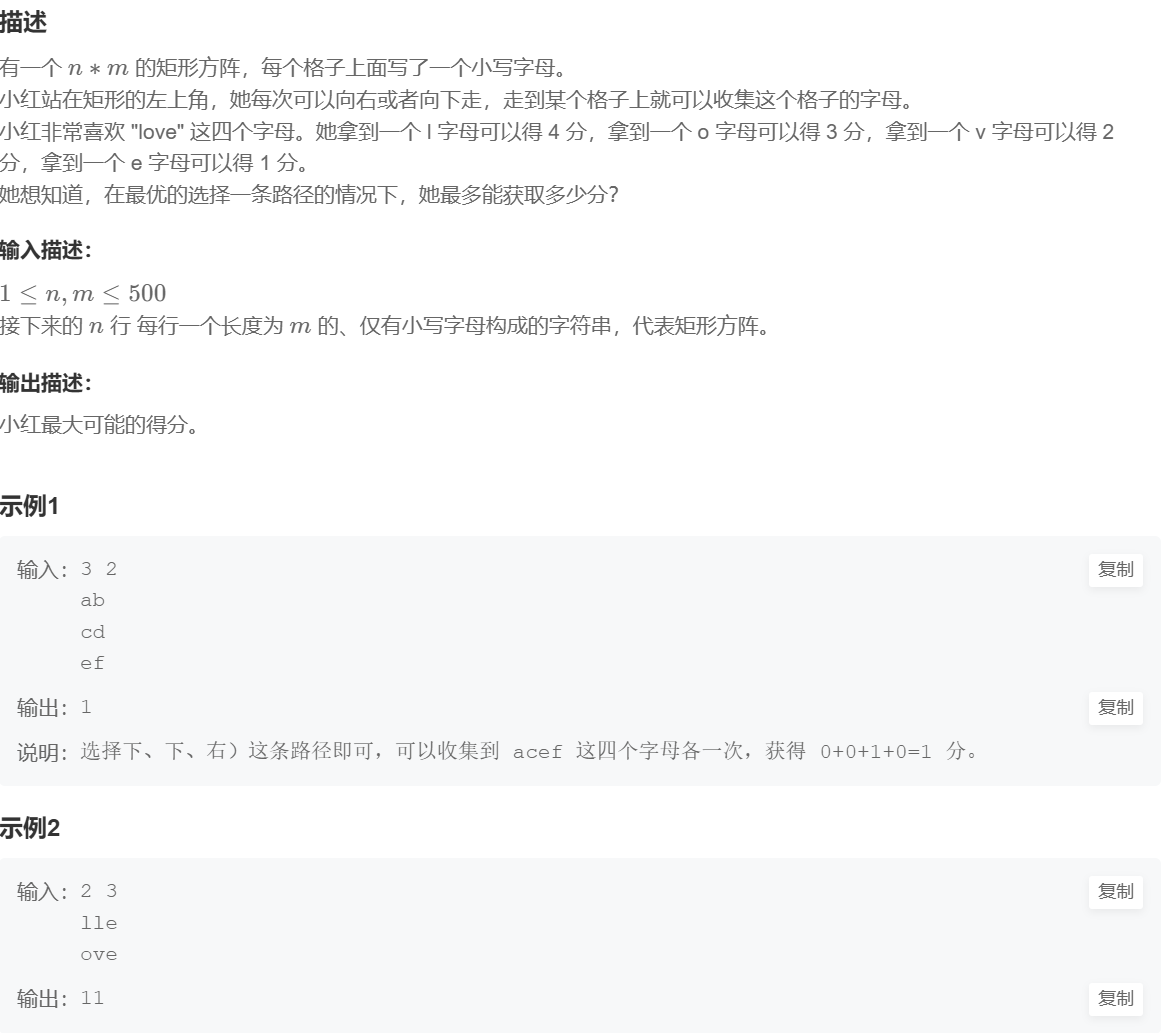
#include <iostream>
using namespace std;

const int n = 1005;
int dp[n][n];

int main() {
	int n, m;
	cin >> n >> m;
	char ch;
	for (int i = 0; i < n; i++){
		for (int j = 0; j < m; j++){
			cin >> ch;
			if (ch == 'l') dp[i][j] = 4;
			else if (ch == 'o') dp[i][j] = 3;
			else if (ch == 'v') dp[i][j] = 2;
			else if (ch == 'e') dp[i][j] = 1;
			else a[i][j] = 0;
		}
	}

for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + dp[i][0]; 
for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + dp[0][j]; 

	for (int i = 1; i < n; i++){
		for (int j = 1; j < m; j++){
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];
		}
	}

	cout << dp[n - 1][m - 1] << endl;
	return 0;
}

2、[noip2002 普及组] 过河卒

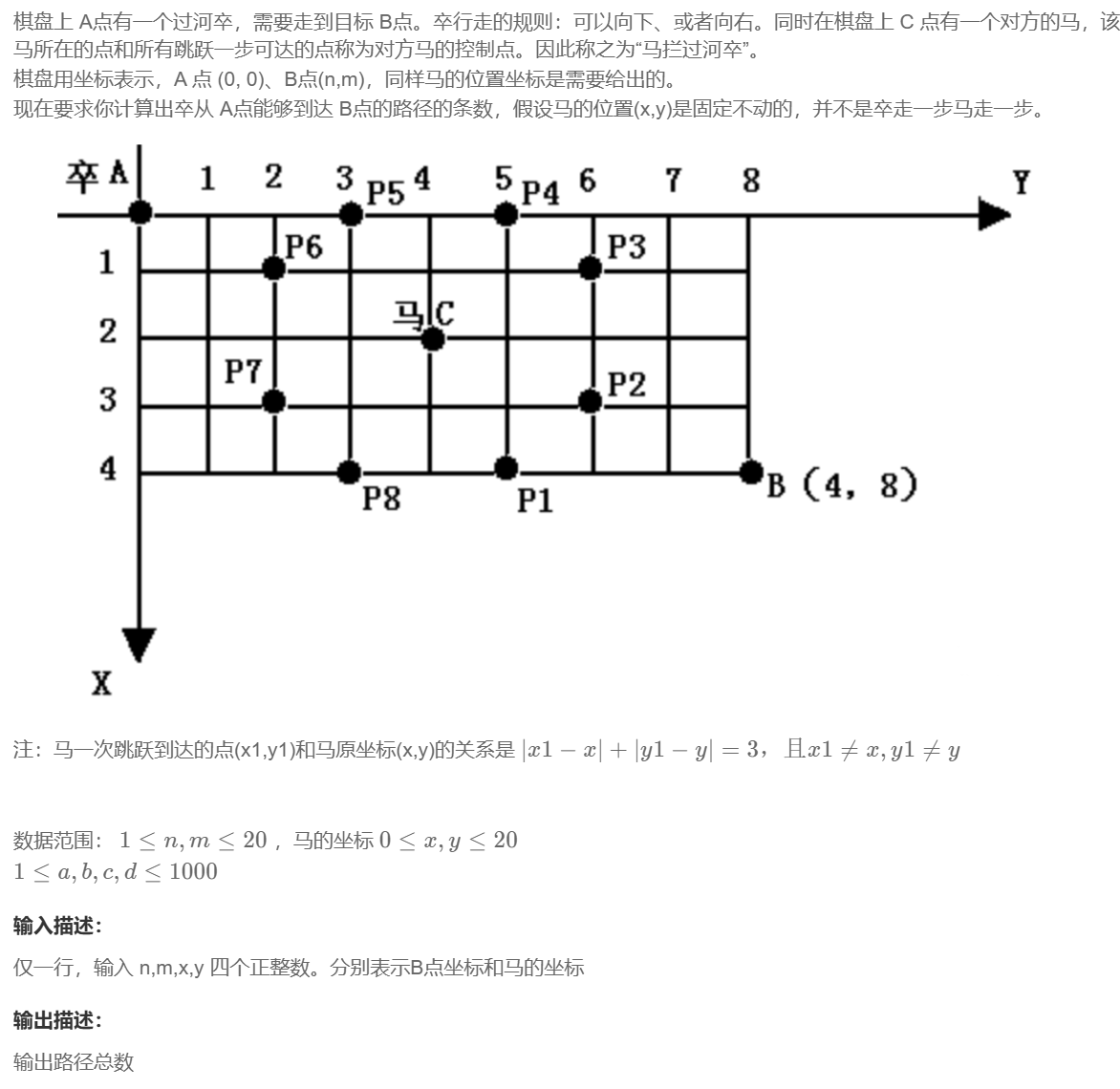
分析：

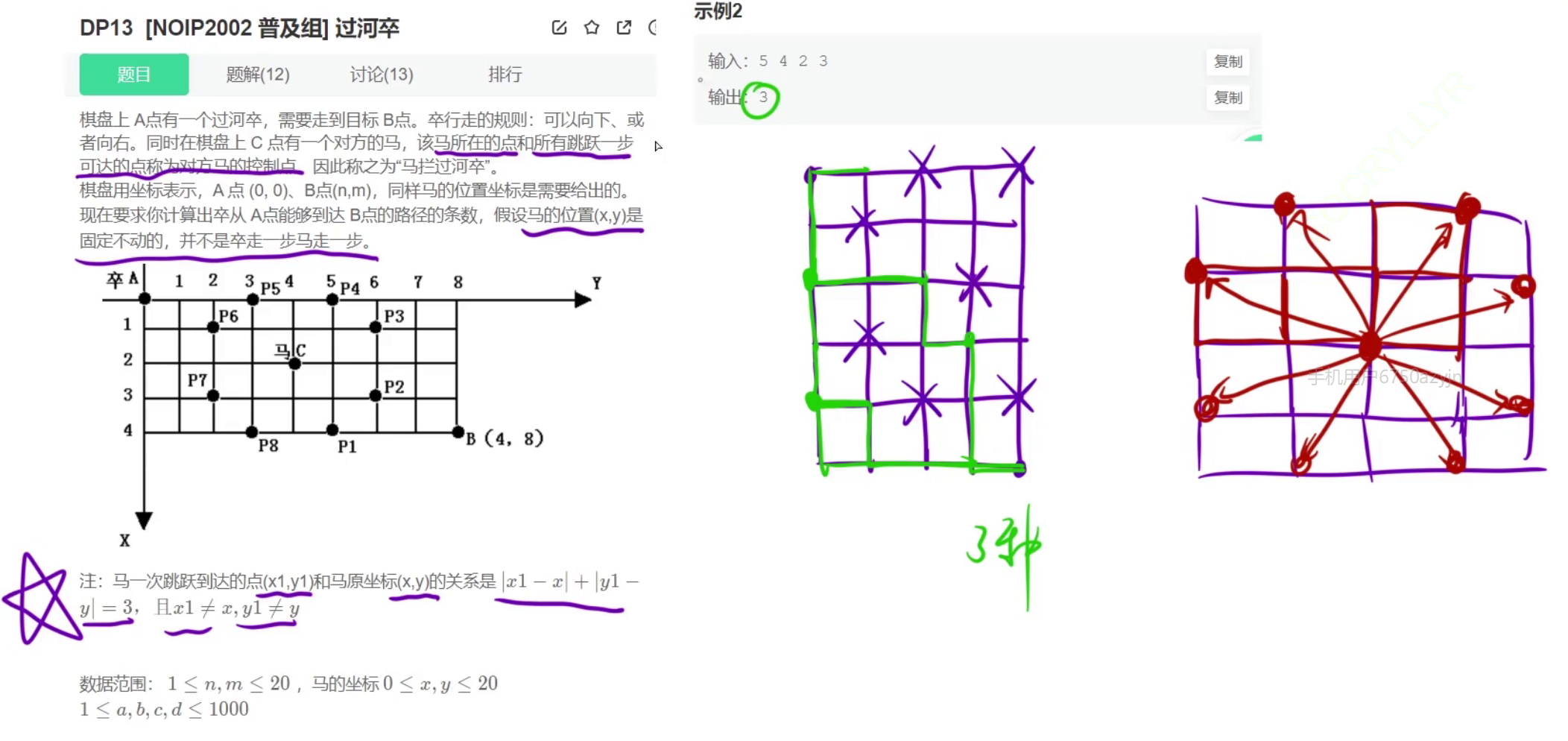
#include <iostream>
#include <vector>
using namespace std;

//int dp[1005][1005];
int main()
{
    int n, m, x, y;
    cin >> n >> m >> x >> y;
    
    vector<vector<long long>> dp(n + 2, vector<long long>(m + 2));
    dp[0][1] = 1;
    x += 1, y += 1;和dp表位置一一对应

    for (int i = 1; i <= n + 1; i++)
    {
        for (int j = 1; j <= m + 1; j++) { //马所在位置
            if (i != x && j != y && abs(i - x) + abs(j - y) == 3 || (i == x && j == y))
            {
                dp[i][j] == 0;
            }
            else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    cout << dp[n + 1][m + 1] << endl;

    return 0;
}

二、子序列和连续序列类

1. mari和shiny

#include <iostream>
#include <string>
using namespace std;
typedef long long ll;
int main()
{
	int n;
	string str;
	cin >> n >> str;
	ll s = 0, h = 0, y = 0;
	for (int i = 0; i < n; i++) {
		if (str[i] == 's') s++;
		else if (str[i] == 'h') h += s;
		else if (str[i] == 'y') y += h;
	}
	cout << y << endl;
	return 0;
}

#include <iostream>
#include <vector>
 
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    string str;
    cin >> str;
    string t="shy";
    int m=t.size();
 
    vector<vector<long long>> dp(n+1, vector<long long>(m+1));
    for(int i=0; i<=n; i++) dp[i][0]=1;
 
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            if(str[i-1]==t[j-1])
                dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
            else
                dp[i][j]=dp[i-1][j];
        }
    }
 
    cout << dp[n][m] << endl;
 
    return 0;
}

2. 不同的子序列


int numdistinct(string s, string t) {
	int n = s.size(), m = t.size();
	if (n < m) return 0;
	vector<vector<unsigned int>> dp(n + 1, vector<unsigned int>(m + 1)); //注意是unsigned int
	for (int i = 0; i <= n; i++) dp[i][0] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			dp[i][j] = dp[i - 1][j] +(s[i - 1] == t[j - 1] ? dp[i - 1][j - 1] : 0);
		}
	}
	return dp[n][m];
}