【数据结构与算法】Kadane‘s算法（动态规划、最大子数组和）_算法

文章目录

一、算法原理
二、例题
- 2.1 最大子数组和
- 2.2 环形子数组的最大和

一、算法原理

kadane's算法是一种用于解决最大子数组和问题的动态规划算法。这类问题的目标是在给定整数数组中找到一个连续的子数组，使其元素之和最大（数组含有负数）。

算法的核心思想是通过迭代数组的每个元素，维护两个变量来跟踪局部最优解和全局最优解。

以下是kadane’s算法的详细步骤：

初始化：
- 令 maxendinghere 表示在当前位置结束的最大子数组和，初始值为数组的第一个元素。
- 令 maxsofar 表示全局最大子数组和，初始值也为数组的第一个元素。
迭代：
- 从数组的第二个元素开始迭代。
- 对于每个元素，计算在当前位置结束的最大子数组和：
  maxendinghere = max(nums[i], maxendinghere + nums[i]);
  这表示要么继续当前子数组，要么从当前位置开始一个新的子数组。
- 更新全局最大子数组和：
  maxsofar = max(maxsofar, maxendinghere);
  如果在当前位置结束的子数组和大于全局最大和，更新全局最大和。
返回结果：
- 当迭代完成后，maxsofar 中存储的即为最大子数组和。

复杂度：

时间复杂度：o(n)，其中 n 为 nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度：o(1)。我们只需要常数空间存放若干变量。

图例：
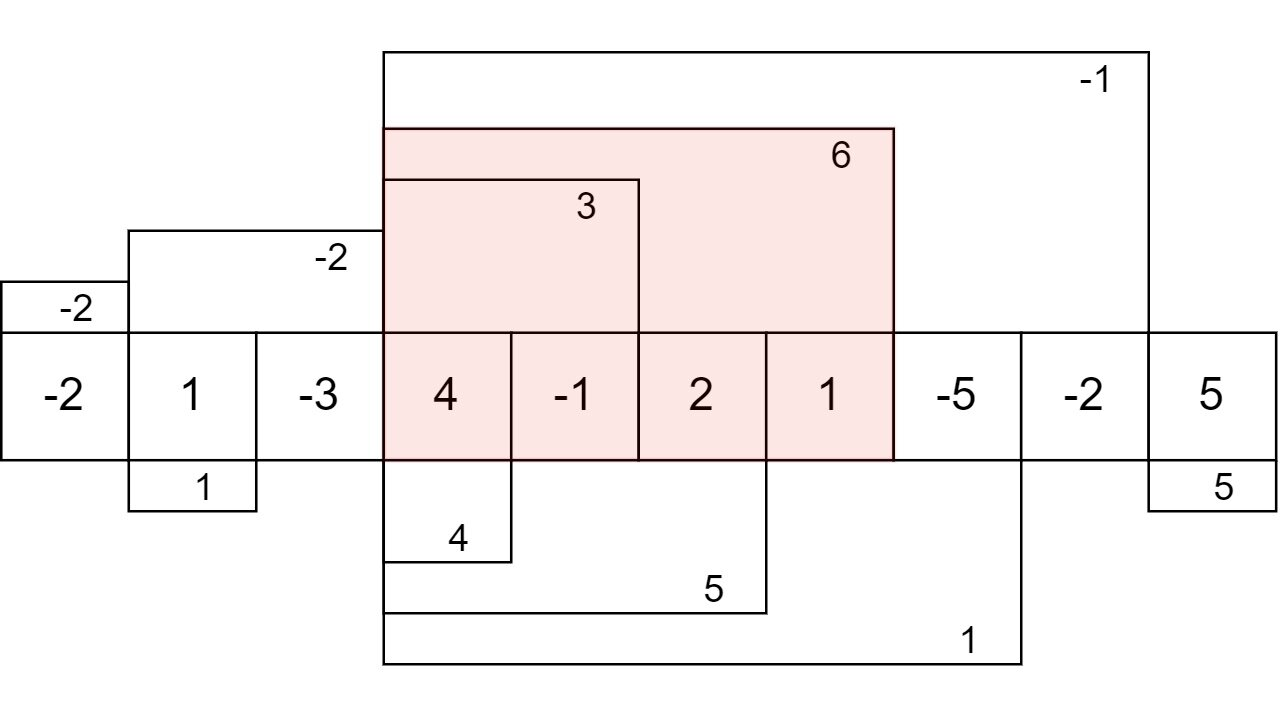
在这里插入图片描述

简要说明：（如过当前值比前面的局部最大值+当前值还大，那么就从当前值开始继续计算局部最大值）

i=0,maxendinghere 、maxsofar 初始值都为数组第一个元素，-2；
开始循环，i=1，maxendinghere = max(nums[1], maxendinghere + nums[1])，即maxendinghere = max(1, -2 + 1)=1，maxsofar=1；
i=2， maxendinghere = max(nums[2], maxendinghere + nums[2])，即maxendinghere = max(-3, 1 - 3)=-2，maxsofar=1；
i=3，maxendinghere = max(nums[3], maxendinghere + nums[3])，即maxendinghere = max(4, -2 + 4)=4，maxsofar=4；
…

二、例题

2.1 最大子数组和

在这里插入图片描述

解答：

int maxsubarray(int* nums, int numssize) {
    int maxendinghere  = nums[0], maxsofar = nums[0];
    for (int i = 1; i < numssize; i++) {
        maxendinghere  = fmax(maxendinghere  + nums[i], nums[i]);
        maxsofar = fmax(maxsofar, maxendinghere );
    }
    return maxsofar;
}

简单换个写法：

int maxsubarray(int* nums, int numssize) {
    int maxendinghere  = nums[0], maxsofar = nums[0];
    for (int i = 1; i < numssize; i++) {
        maxendinghere  = maxendinghere  + nums[i]>nums[i]?maxendinghere  + nums[i]:nums[i];
        maxsofar = maxsofar>maxendinghere?maxsofar:maxendinghere;
    }
    return maxsofar;
}

2.2 环形子数组的最大和

在这里插入图片描述

解答：

int maxsubarraysumcircular(int* nums, int numssize) {
    if (nums == null || numssize == 0) return 0;
    int maxsum = nums[0], minsum = nums[0];
    int maxcur = nums[0], mincur = nums[0];
    int sum = nums[0];

    for (int i = 1; i < numssize; i++) {
        sum += nums[i];
        maxcur = fmax(nums[i], maxcur + nums[i]);
        mincur = fmin(nums[i], mincur + nums[i]);
        maxsum = fmax(maxsum, maxcur);
        minsum = fmin(minsum, mincur);
    }

    if (maxsum < 0) return maxsum; // 如果所有数都是负数，返回最大值
    return fmax(maxsum, sum - minsum); // 返回“不跨越头尾的最大子数组和”和“跨越头尾的最大子数组和”中的较大者
}