目录
一.插入排序
1.概念介绍
2.动态+静态解析



3.代码实现
void insertsort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else break;
}
a[end + 1] = tmp;
}
}
二.冒泡排序
1.概念介绍
2.动态+静态解析
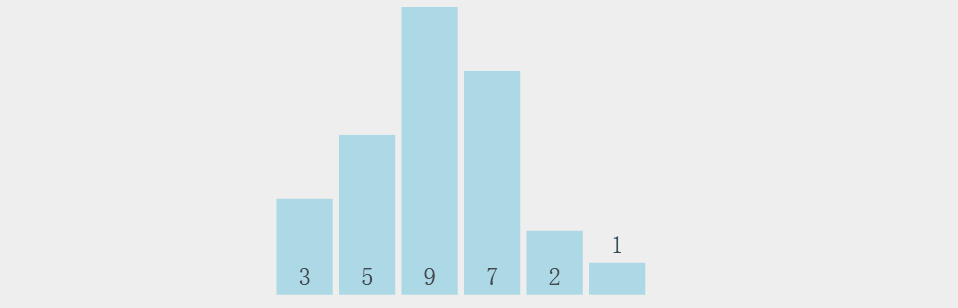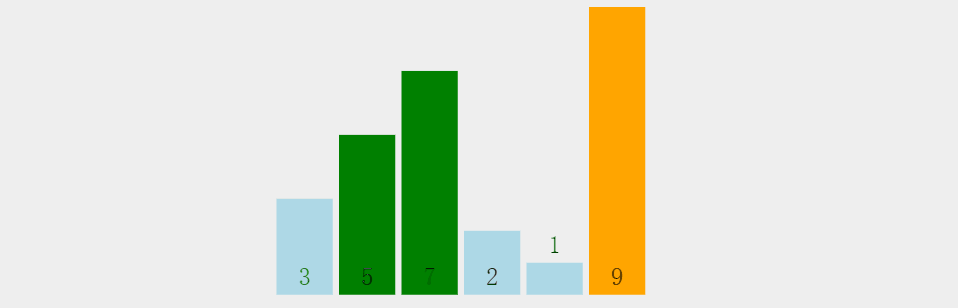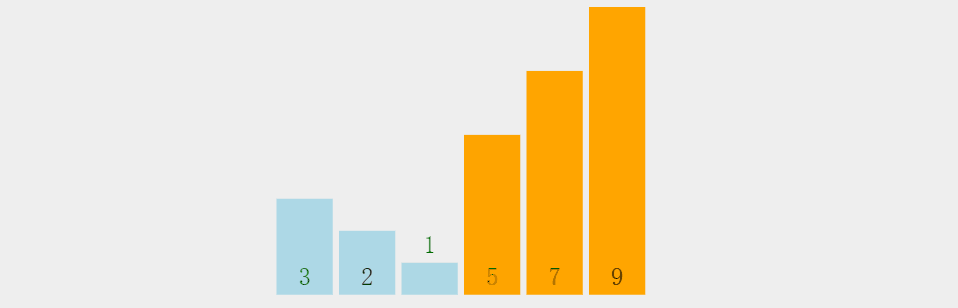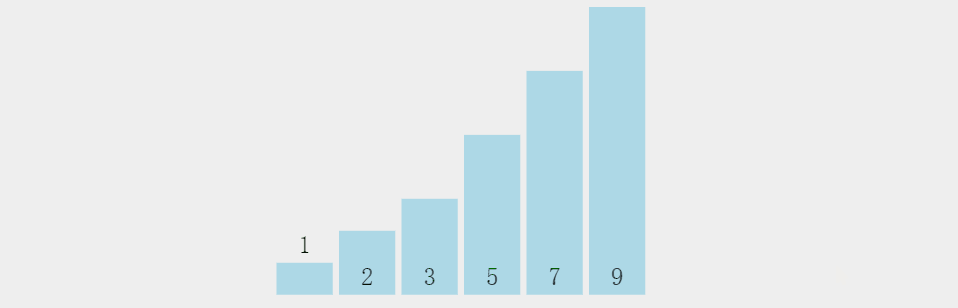
3.代码示例
void bubblesort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
}
}
}
}4.番外
三.选择排序
1.概念介绍
2.动态+静态解析

3.代码示例
void selectsort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int maxi = begin;
int mini = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[mini] > a[i])
mini = i;
if (a[maxi] < a[i])
maxi = i;
}
swap(&a[mini], &a[begin]);
if (maxi == begin)
maxi = mini;
swap(&a[maxi], &a[end]);
begin++;
end--;
}
}四.希尔排序
1.概念介绍
2.动态+静态解析
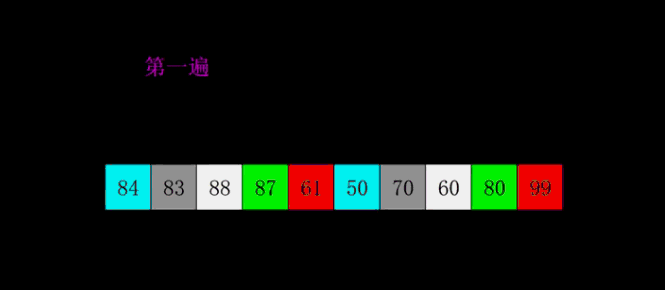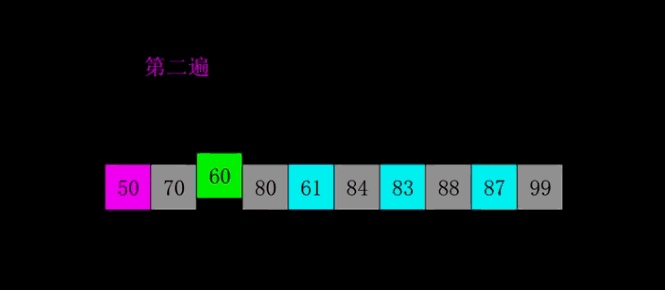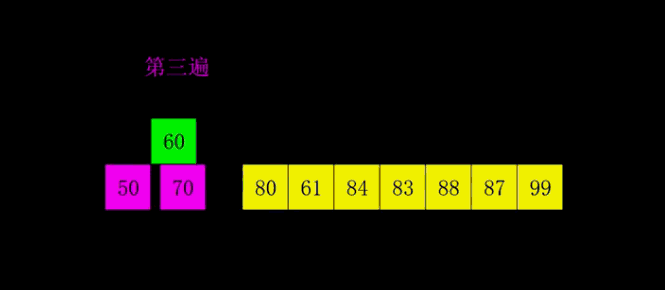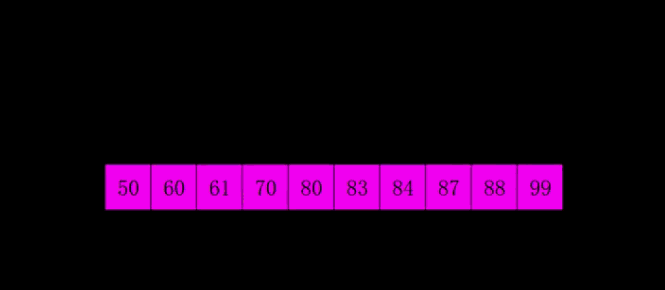
3.代码示例
void shellsort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else break;
}
a[end + gap] = tmp;
}
}
}4.番外
五.堆排序
1.概念介绍
2.静态解析
3.代码示例
void adjustdown(int* a, int parent, int n)
{
int children = 2 * parent + 1;
while (children < n)
{
if (children + 1 < n && a[children] < a[children + 1])
children++;
if (a[parent] < a[children])
{
swap(&a[parent], &a[children]);
parent = children;
children = 2 * parent + 1;
}
else break;
}
}
void heapsort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
adjustdown(a, i, n);
}
printarray(a, 10);
int end = n;
while (end > 0)
{
swap(&a[end - 1], &a[0]);
end--;
adjustdown(a, 0, end);
}
}六.快速排序
1.概念介绍
2.动态+静态解析
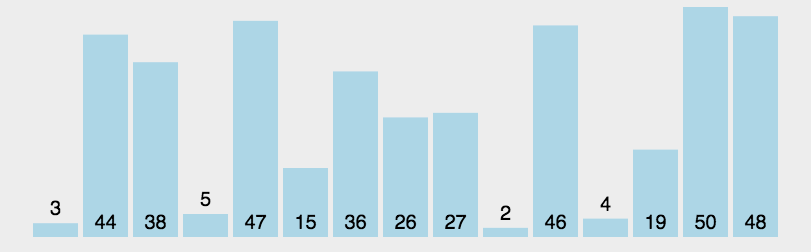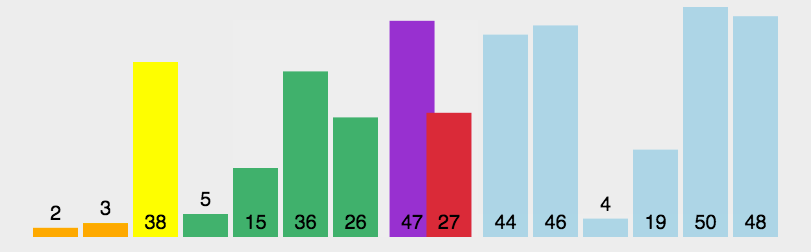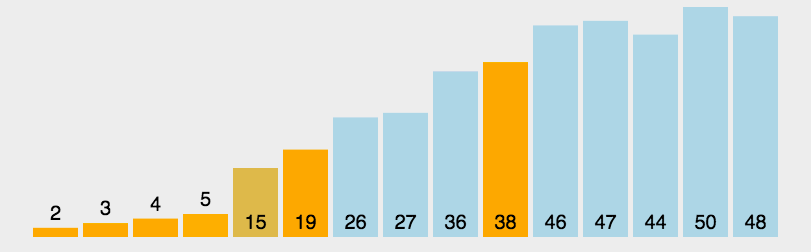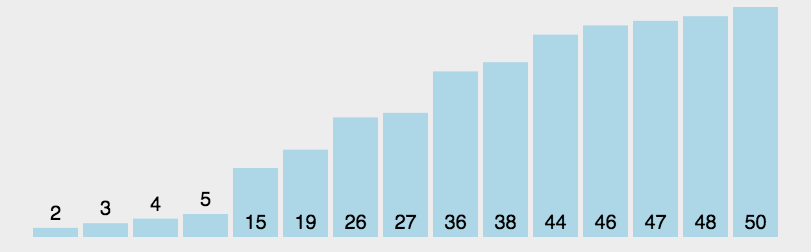
2.1霍尔法
2.2挖坑法
2.3前后指针法
3.代码实现
3.1霍尔法
void quicksortbyhoare(int* a, int begin, int end)
{
if (begin >= end)
return;
int left = begin;
int right = end;
//三数取中法取key
int key = midi(a, left, right);
swap(&a[left], &a[key]);
while (left < right)
{
while (left < right && a[right] >= a[key])
right--;
while (left < right && a[left] <= a[key])
left++;
swap(&a[left], &a[right]);
}
swap(&a[left], &a[key]);
key = left;
quicksortbyhoare(a, 0, key - 1);
quicksortbyhoare(a, key + 1, end);
}3.2挖坑法
void quicksortbydigging(int* a, int begin, int end)
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = left;
int tmp = a[key];
while (left < right)
{
while (left < right && a[key] <= a[right])
right--;
if (left < right)
a[left] = a[right];
while (left < right && a[key] >= a[left])
left++;
if (left < right)
a[right] = a[left];
}
a[left] = tmp;
key = left;
quicksortbydigging(a, 0, key - 1);
quicksortbydigging(a, key + 1, end);
}3.3前后指针法
void quicksortbypoints(int* a, int begin, int end)
{
if (begin >= end)
return;
int prev = begin;
int cur = prev + 1;
int key = begin;
while (cur <= end)
{
if (a[cur] < a[key] && ++prev != cur)
swap(&a[cur], &a[prev]);
cur++;
}
swap(&a[prev], &a[key]);
key = prev;
quicksortbypoints(a, 0, key - 1);
quicksortbypoints(a, key + 1, end);
}4.思路优化
4.1key的优化
把快速排序看成一个二叉树结构,树的高度一般为logn,时间复杂度为o(nlogn)
但对于一个有序数列或接近于有序的数列,key如果每次都取最左边或最右边.那么树的高度就会接近于n,时间复杂度就会变为o(n^2),这时快速排序的效率会大大减少,那么归根结底还是key的取法有问题,所以下面我们针对key的取法进行优化
4.1.1随机数取key
int key = rand() % (right - left);
key += left;4.1.2三数取中法
int midi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] < a[right])
return right;
else return left;
}
else
{
if (right < a[mid])
return mid;
else if (a[left] < a[right])
return left;
else return right;
}
}4.2递归的优化
我们都知道递归需要频繁的创建函数栈帧,那么如果递归深度太高就有可能导致栈溢出,而操作系统提供给我们的栈的大小大约为8000000字节,所以我们可以考虑自己建一个栈来实现递归的效果
不会手撕栈的可以看我这篇文章
void quicksortbystack(int* a, int begin, int end)
{
stack st;
initstack(&st);
pushstack(&st, end);
pushstack(&st, begin);
while (!isempty(&st))
{
int left = topstack(&st);
popstack(&st);
int right = topstack(&st);
popstack(&st);
int prev = left;
int cur = prev + 1;
int key = left;
while (cur <= right)
{
if (a[cur] < a[key])
swap(&a[cur], &a[prev]);
cur++;
}
swap(&a[prev], &a[key]);
key = prev;
//left, key - 1 key key + 1, right
if (left < key - 1)
{
pushstack(&st, key - 1);
pushstack(&st, left);
}
if (key + 1 < right)
{
pushstack(&st, right);
pushstack(&st, key + 1);
}
}
destroystack(&st);
}七.归并排序
1.概念介绍
2.动态解析+静态解析

2.1递归法
2.2非递归法
3.代码实现
3.1递归法
void _mergesort(int* a, int begin, int end, int* temp)
{
if (begin >= end)
return;
//将区间分为左右两半
int mid = (begin + end) / 2;
//[begin,end]--->[begin , mid ] [mid+1,end]
//开始递归拆开
_mergesort(a, begin, mid, temp);
_mergesort(a, mid+1, end, temp);
//合并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
//i要从相对位置起
int i = begin1;
//如果两个区间有一个结束,就停止比较归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
//使用两个while将未归并完的数组进行追加
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
//拷贝回去要使用相对位置
memcpy(a+begin, temp+begin, (end-begin+1)*sizeof(int));
}
void mergesort(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
//使用一个子函数进行排序
_mergesort(a, 0, n - 1, temp);
free(temp);
}3.2非递归法
void mergesortnonr(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
int gap = 1;
//i 是要两组两组的跳过
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//区间 [i , i+gap-1] [i+gap,i+2*gap-1]
//合并
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//i要从相对位置起
int j = begin1;
//如果两个区间有一个结束,就停止比较归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
}
memcpy(a, temp, n * sizeof(int));
gap *= 2;
}
}






发表评论