概述
logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘x+b,其中w和b是待求参数,其区别在于他们的因变量不同,多重线性回归直接将w‘x+b作为因变量,即y =w‘x+b,而logistic回归则通过函数l将w‘x+b对应一个隐状态p,p =l(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果l是logistic函数,就是logistic回归,如果l是多项式函数就是多项式回归。
logistic回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。
logistic回归模型的适用条件
- 1 因变量为二分类的分类变量或某事件的发生率,并且是数值型变量。但是需要注意,重复计数现象指标不适用于logistic回归。
- 2 残差和因变量都要服从二项分布。二项分布对应的是分类变量,所以不是正态分布,进而不是用最小二乘法,而是最大似然法来解决方程估计和检验问题。
- 3 自变量和logistic概率是线性关系
- 4 各观测对象间相互独立。
原理
线性回归
线性回归是一种使用特征属性的线性组合来预测响应的方法。它的目标是找到一个线性函数,以尽可能准确地描述特征或自变量(x)与响应值(y)之间的关系,使得预测值与真实值之间的误差最小化。
在数学上,线性回归要找的这个线性函数叫回归方程,其定义如下:

ps:损失函数的系数 1/2 是为了便于计算,使对平方项求导后的常数系数为 1。

现代机器学习中常用的参数更新方法是梯度下降法。
梯度下降法

- 批梯度下降(bgd):批梯度下降会获得全局最优解,缺点是在更新每个参数的时候需要遍历所有的数据,计算量会很大,并且会有很多的冗余计算,导致的结果是当数据量大的时候,每个参数的更新都会很慢。
- 随机梯度下降(sgd):随机梯度下降是以高方差频繁更新,优点是使得sgd会跳到新的和潜在更好的局部最优解,缺点是使得收敛到局部最优解的过程更加的复杂。
- 小批量梯度下降(mgbd):小批量梯度下降结合了sgd和batch gd的优点,每次更新的时候使用n个样本。减少了参数更新的次数,可以达到更加稳定收敛结果,一般在深度学习当中我们采用这种方法。
回归的评价指标

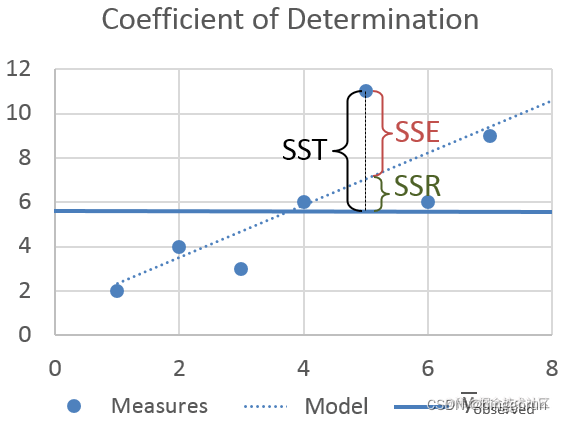
从图中不难看出,三者的关系是:sst = ssr + sse。如果 ssr 的值等于 sst,这意味着我们的回归模型是完美的。
逻辑回归
逻辑回归和线性回归不同的地方在于:线性回归适用于解决回归问题,而逻辑回归适用于解决分类问题。本节我们就讲讲造成这种差异的原因。
sigmoid函数

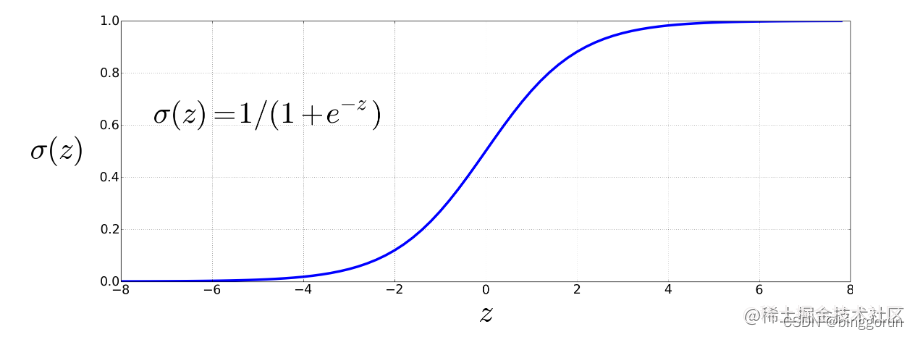


代价函数

梯度下降法求解

逻辑回归的分类
逻辑回归对特征变量(x)和分类响应变量(y)之间的关系进行建模,在给定一组预测变量的情况下,它能给出落入特定类别响应水平的概率。也就是说,你给它一组数据(特征),它告诉你这组数据属于某一类别的概率。根据分类响应变量(y)的性质,我们可以将逻辑回归分为三类:
- 二元逻辑回归(binary logistic regression)
当分类结果只有两种可能的时候,我们就称为二元逻辑回归。例如,考试通过或未通过,回答是或否,血压高或低。 - 名义逻辑回归(nominal logistic regression)
当存在三个或更多类别且类别之间没有自然排序时,我们就称为名义逻辑回归。例如,企业的部门有策划、销售、人力资源等,颜色有黑色、红色、蓝色、橙色等。 - 序数逻辑回归(ordinal logistic regression)
当存在三个或更多类别且类别之间有自然排序时,我们就称为序数逻辑回归。例如,评价有好、中、差,身材有偏胖、中等、偏瘦。注意,类别的排名不一定意味着它们之间的间隔相等。
softmax regression

原为链接:https://www.cnblogs.com/marvin-wen/p/15966151.html
优劣势
优点
1)形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大
2)模型效果不错。在工程上是可以接受的(作为baseline),如果特征工程做的好,效果不会太差,并且特征工程可以大家并行开发,大大加快开发的速度。
3)训练速度较快。分类的时候,计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
4)资源占用小,尤其是内存。因为只需要存储各个维度的特征。
5)方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果,因为输出的是每个样本的概率分数,我们可以很容易的对这些概率分数进行cutoff,也就是划分阈值(大于某个阈值的是一类,小于某个阈值的是一类)。
缺点
1)准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。
2)很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。
3)处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。
4)逻辑回归本身无法筛选特征。有时候,我们会用gbdt来筛选特征,然后再上逻辑回归。
实现
评分卡的目标模型是,依据客户数据,预测客户是否坏客户
整个建模过程共5步:
scikit-learn
在scikit-learn中,与逻辑回归有关的主要是这3个类。logisticregression, logisticregressioncv 和logistic_regression_path。其中logisticregression和logisticregressioncv的主要区别是logisticregressioncv使用了交叉验证来选择正则化系数c。而logisticregression需要自己每次指定一个正则化系数。除了交叉验证,以及选择正则化系数c以外, logisticregression和logisticregressioncv的使用方法基本相同。
logistic_regression_path类则比较特殊,它拟合数据后,不能直接来做预测,只能为拟合数据选择合适逻辑回归的系数和正则化系数。主要是用在模型选择的时候。一般情况用不到这个类
此外,scikit-learn里面有个容易让人误解的类randomizedlogisticregression,虽然名字里有逻辑回归的词,但是主要是用l1正则化的逻辑回归来做特征选择的,属于维度规约的算法类,不属于我们常说的分类算法的范畴。
后面的讲解主要围绕logisticregression和logisticregressioncv中的重要参数的选择来来展开,这些参数的意义在这两个类中都是一样的。
函数调用形式:
logisticregression(penalty='l2',dual=false,tol=1e4,c=1.0,fit_intercept=true,
intercept_scaling=1,class_weight=none,random_state=none,solver='liblinear',
max_iter=100,multi_class='ovr',verbose=0,warm_start=false, n_jobs=1)
参数
| 参数 | 参数名称 | 解释 |
|---|---|---|
| penalty | 正则化类型 | 1)字符串型,’l1’ or ‘l2’,默认:’l2’;正则化类型。 2)logisticregression和logisticregressioncv默认就带了正则化项。penalty参数可选择的值为"l1"和"l2".分别对应l1的正则化和l2的正则化,默认是l2的正则化。 3)penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择,如果是l2正则化,那么4种可选的算法{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}都可以选择。但是如果penalty是l1正则化的话,就只能选择‘liblinear’了。这是因为l1正则化的损失函数不是连续可导的,而{‘newton-cg’, ‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。 |
| dual | 布尔型,默认:false。当样本数>特征数时,令dual=false;用于liblinear解决器中l2正则化。 | |
| tol | 误差范围 | 浮点型,默认:1e-4;迭代终止判断的误差范围。 |
| c | 正则化强度 | 浮点型,默认:1.0;其值等于正则化强度的倒数,为正的浮点数。数值越小表示正则化越强。 |
| fit_intercept | 截距 | 布尔型,默认:true;指定是否应该向决策函数添加常量(即偏差或截距)。 |
| intercept_scaling | intercept_scaling | 浮点型,默认为1;仅仅当solver是”liblinear”时有用。 |
| solver | 逻辑回归损失函数的优化方法 | solver参数决定了我们对逻辑回归损失函数的优化方法,有4种算法可以选择,分别是: a. liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。 b.lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。 c. newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。 d. sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候,sag是一种线性收敛算法,这个速度远比sgd快。 从上面的描述可以看出,newton-cg, lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的l1正则化,只能用于l2正则化。而liblinear通吃l1正则化和l2正则化。 同时,sag每次仅仅使用了部分样本进行梯度迭代,所以当样本量少的时候不要选择它,而如果样本量非常大,比如大于10万,sag是第一选择。但是sag不能用于l1正则化,所以当你有大量的样本,又需要l1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量,要么回到l2正则化。 |
| max_iter | 最大迭代次数 | 整型,默认是100; |
| multi_class | 分类方式 | multi_class参数决定了我们分类方式的选择,有 ovr和multinomial两个值可以选择,默认是 ovr。如果是二元逻辑回归,ovr和multinomial并没有任何区别,区别主要在多元逻辑回归上。 |
| verbose | 整型,默认是0;对于liblinear和lbfgs solver,verbose可以设为任意正数。 | |
| class_weight | 分类模型中各种类型的权重 | class_weight参数用于标示分类模型中各种类型的权重,可以不输入,即不考虑权重,或者说所有类型的权重一样。如果选择输入的话,可以选择balanced让类库自己计算类型权重,或者我们自己输入各个类型的权重,比如对于0,1的二元模型,我们可以定义class_weight={0:0.9, 1:0.1},这样类型0的权重为90%,而类型1的权重为10%。 如果class_weight选择balanced,那么类库会根据训练样本量来计算权重。某种类型样本量越多,则权重越低,样本量越少,则权重越高。 sklearn的官方文档中,当class_weight为balanced时,类权重计算方法如下:n_samples / (n_classes * np.bincount(y))_samples为样本数,n_classes为类别数量,np.bincount(y)会输出每个类的样本数,例如y=[1,0,0,1,1],则np.bincount(y)=[2,3] |
| sample_weight | 样本权重 | 由于样本不平衡,导致样本不是总体样本的无偏估计,从而可能导致我们的模型预测能力下降。遇到这种情况,我们可以通过调节样本权重来尝试解决这个问题。调节样本权重的方法有两种: 第一种是在class_weight使用balanced。 第二种是在调用fit函数时,通过sample_weight来自己调节每个样本权重。 在scikit-learn做逻辑回归时,如果上面两种方法都用到了,那么样本的真正权重是class_weight*sample_weight。 |
| warm_start | 布尔型,默认为false;当设置为true时,重用前一个调用的解决方案以适合初始化。否则,只擦除前一个解决方案。对liblinear解码器无效。 | |
| n_jobs | 使用的cpu核数 | 整型,默认是1;如果multi_class=‘ovr’ ,则为在类上并行时使用的cpu核数。无论是否指定了multi_class,当将’ solver ’ '设置为’liblinear’时,将忽略此参数。如果给定值为-1,则使用所有核。 |
| random_state | 随机种子 | 整型,默认none;当“solver”==“sag”或“liblinear”时使用。在变换数据时使用的伪随机数生成器的种子。如果是整数, random_state为随机数生成器使用的种子;若为randomstate实例,则random_state为随机数生成器;如果没有,随机数生成器就是’ np.random '使用的randomstate实例。 |
toad:基于 python 的标准化评分卡模型
原为链接:https://geekdaxue.co/read/fcant@ai/he3tkz
本次和大家分享一个开源的评分卡神器toad。从数据探索、特征分箱、特征筛选、特征woe变换、建模、模型评估、转换分数,都做了完美的包装,极大的简化了建模人员的门槛。
一、读取数据、划分样本集
首先通过read_csv读取数据,看看数据概况。
data = pd.read_csv('train.csv')
print('shape:',data.shape)
data.head(10)
#>> shape: (108940, 167)
这个测试数据有10万条数据,167个特征。
print('month:',data.month.unique())
#>> month: ['2019-03' '2019-04' '2019-05' '2019-06' '2019-07']
通过观察时间变量,可以发现数据的时间跨度为2019年5月到7月。为了真正测试模型效果,将用3月和4月数据用于训练样本,5月、6月、7月数据作为时间外样本,也叫作oot的跨期样本。
train = data.loc[data.month.isin(['2019-03','2019-04'])==true,:]
oot = data.loc[data.month.isin(['2019-03','2019-04'])==false,:]
#train = data.loc[data.month.isin(['mar-19','apr-19'])==true,:]
#oot = data.loc[data.month.isin(['mar-19','apr-19'])==false,:]
print('train size:',train.shape,'\noot size:',oot.shape)
#>> train size: (43576, 167)
#>> oot size: (65364, 167)
其实,这部分属于模型设计的阶段,是非常关键的环节。实际工作中会考虑很多因素,要结合业务场景,根据样本量、可回溯特征、时间窗口等因素制定合适的观察期、表现期、以及样本,并且还要定义合适的y标签。本次主要介绍toad的用法,上面的设计阶段先忽略掉。
二、eda相关功能
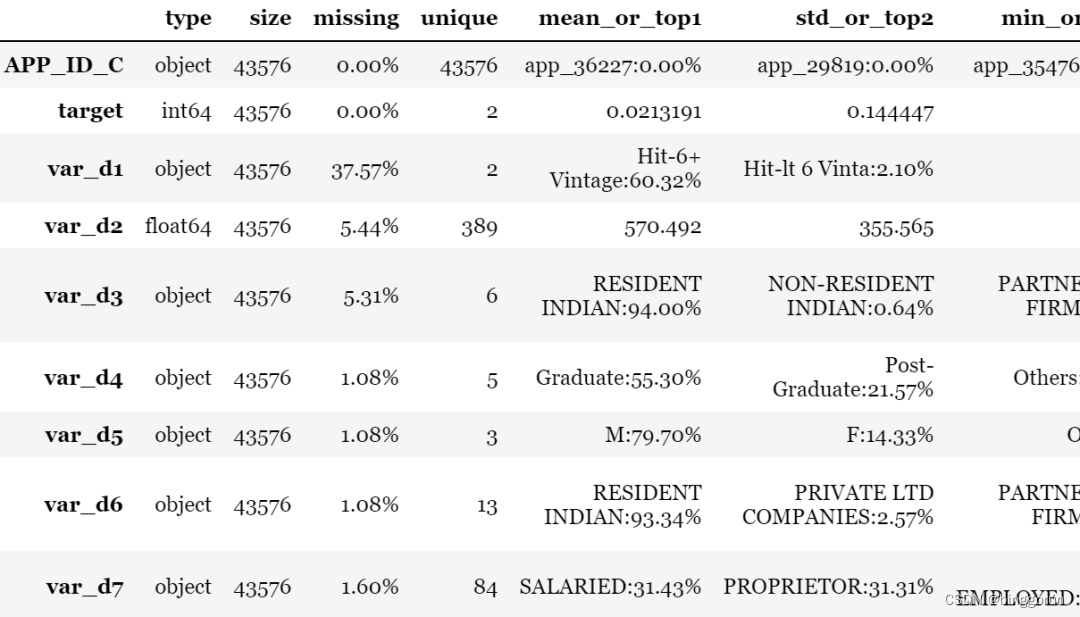
1. toad.detect
eda也叫数据探索分析,主要用于检测数据情况。toad输出每列特征的统计性特征和其他信息,主要的信息包括:缺失值、unique values、数值变量的平均值、离散值变量的众数等。
toad.detect(train)[:10]
2. toad.quality
这个功能主要用于进行变量的筛选,可以直接计算各种评估指标,如iv值、gini指数,entropy熵,以及unique values,结果以iv值排序。target为目标列,iv_only决定是否只输出iv值。
to_drop = ['app_id_c','month'] # 去掉id列和month列
toad.quality(data.drop(to_drop,axis=1),'target',iv_only=true)[:15]
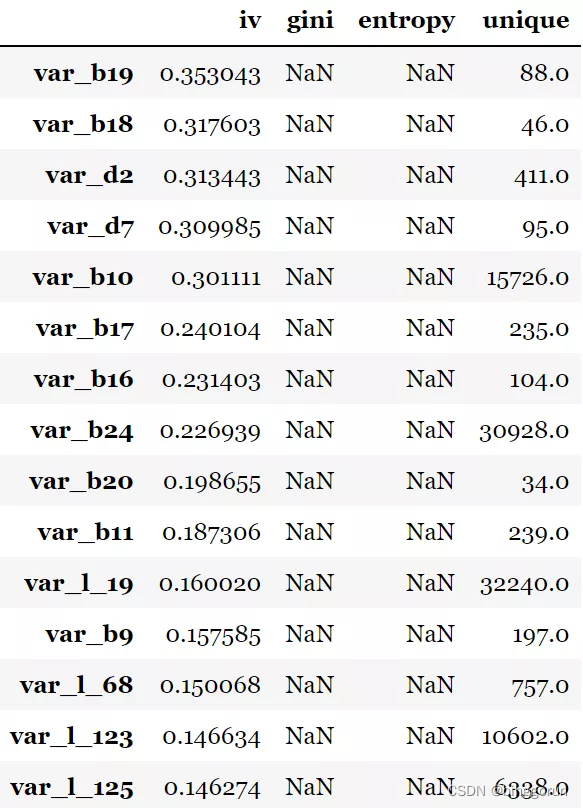
注意:1. 对于数据量大或高维度数据,建议使用iv_only=true 2. 要去掉主键,日期等高unique values且不用于建模的特征
但是,这一步只是计算指标而已,呈现结果进行分析,还并没有真的完成筛选的动作。
三、特征筛选
toad.selection.select
前面通过eda检查过数据质量后,会有选择的筛选一些样本和变量,比如缺失值比例过高的、iv值过低的、相关性太强的等等。
用法很简单,只要通过设置以下几个参数阈值即可实现,如下:
train_selected, dropped = toad.selection.select(train,target = 'target', empty = 0.5, iv = 0.05, corr = 0.7, return_drop=true, exclude=['app_id_c','month'])
print(dropped)
print(train_selected.shape)
经过上面的筛选,165个变量最终保留了32个变量。并且返回筛选过后的dataframe和被删掉的变量列表。
当然了,上面都是一些常规筛选变量的方法,可能有些特殊的变量比如从业务角度很有用是需要保留的,但不满足筛选要求,这时候可以用exclude排除掉。这个功能对于变量初筛非常有用,各种指标直接计算并展示出来。
四、分箱
在做变量的woe变换之前需要做变量的分箱,分箱的好坏直接影响woe的结果,以及变换后的单调性。toad将常用的分箱方法都集成了,包括等频分箱、等距分箱、卡方分箱、决策树分箱、最优分箱等。
并且,toad的分箱功能支持数值型数据和离散型分箱。 这部分东哥看过源码,toad首先判断变量类型,如果为数值型就按数值型分箱处理,如果为非数值型,那么会判断变量唯一值的个数,如果大于10个或者超过变量总数的50%,那么也按照数值型处理。
另外,toad还支持将空值单独分箱处理。
分箱步骤如下:
注意:做筛选时要删去不需要分箱的列,特别是id列和时间列。
# initialise
c = toad.transform.combiner()
# 使用特征筛选后的数据进行训练:使用稳定的卡方分箱,规定每箱至少有5%数据, 空值将自动被归到最佳箱。
c.fit(train_selected.drop(to_drop, axis=1), y = 'target', method = 'chi', min_samples = 0.05) #empty_separate = false
# 为了演示,仅展示部分分箱
print('var_d2:',c.export()['var_d2'])
print('var_d5:',c.export()['var_d5'])
print('var_d6:',c.export()['var_d6'])
#结果输出:
'''
var_d2: [747.0, 782.0, 820.0]
var_d5: [['o', 'nan', 'f'], ['m']]
var_d6: [['public ltd companies', 'non-resident indian', 'private ltd companies', 'partnership firm', 'nan'], ['resident indian', 'trust', 'trust-clubs/assn/soc/sec-25 co.', 'hindu undivided family', 'co-operative societies', 'limited liability partnership', 'association', 'overseas citizen of india', 'trust-ngo']]
'''
观察分箱并调整
因为自动分箱也不可能满足所有需要,很多情况下还是要手动分箱。toad除了上面自动分箱以外,还提供了可视化分箱的功能,帮助调整分箱节点,比如观察变量的单调性。有两种功能:
1. 时间内观察
toad.plot.bin_plot(dataframe, x = none, target = target) #也就是不考虑时间的因素,单纯的比较各个分箱里的bad_rate,观察单调性。
# 看'var_d5'在时间内的分箱
col = 'var_d5'
#观察单个变量分箱结果时,建议设置'labels = true'
bin_plot(c.transform(train_selected[[col,'target']], labels=true), x=col, target='target')
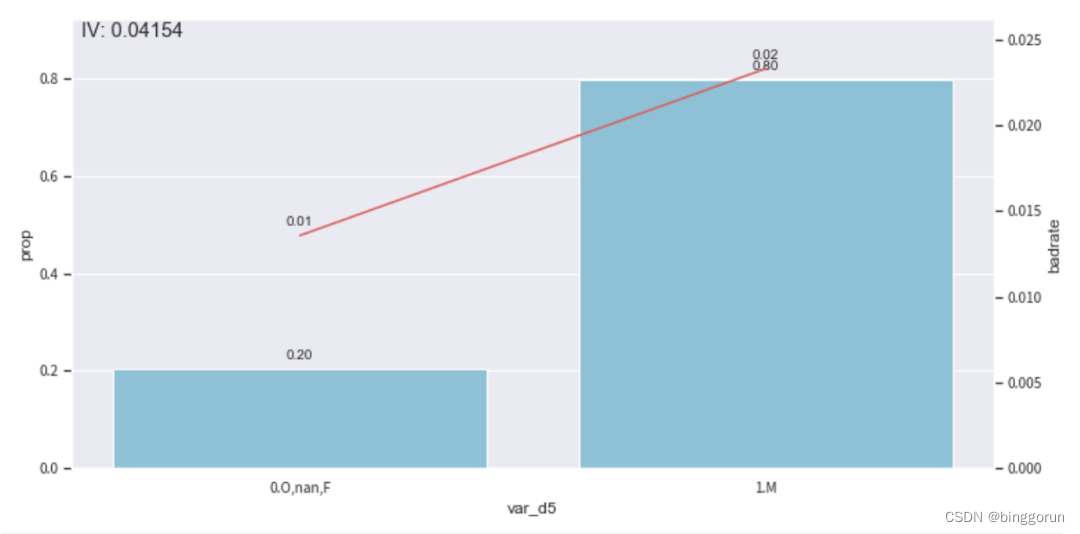
上图中,bar代表了样本量占比,红线代表了坏客户占比。通过观察发现分箱有些不合理,还有调整优化的空间,比如将f和m单独一箱,0和空值分为一箱。因此,使用**c.set_rules(dict)**对这个分箱进行调整。
# iv值较低,假设我们要 'f' 单独分出一组来提高iv
#设置分组
rule = {'var_d5':[['o', 'nan'],['f'], ['m']]}
#调整分箱
c.set_rules(rule)
#查看手动分箱稳定性
bin_plot(c.transform(train_selected[['var_d5','target']], labels=true), x='var_d5', target='target')
badrate_plot(c.transform(oot[['var_d5','target','month']], labels=true), target='target', x='month', by='var_d5')
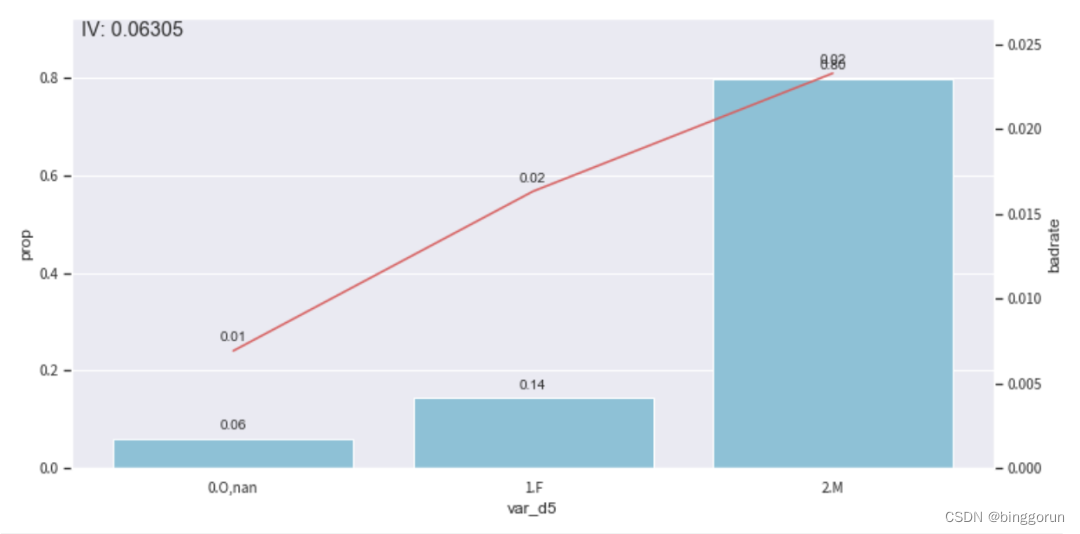
2. 跨时间观察
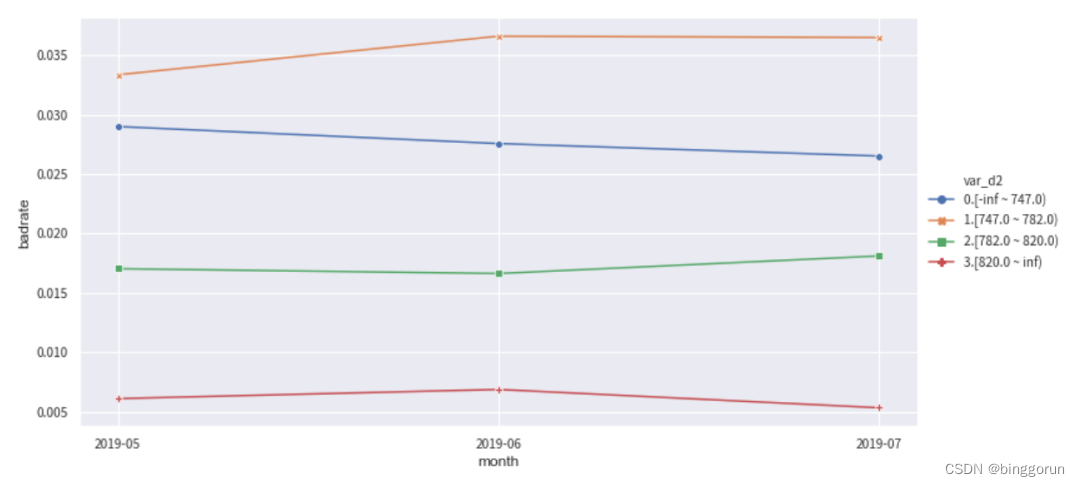
toad.plot.badrate_plot:考虑时间因素,输出不同时间段中每箱的正样本占比,观察分箱随时间变量的稳定性。
- target: 目标列
- x: 时间列, string格式(要预先分好并设成string,不支持timestampe)
- by: 需要观察的特征
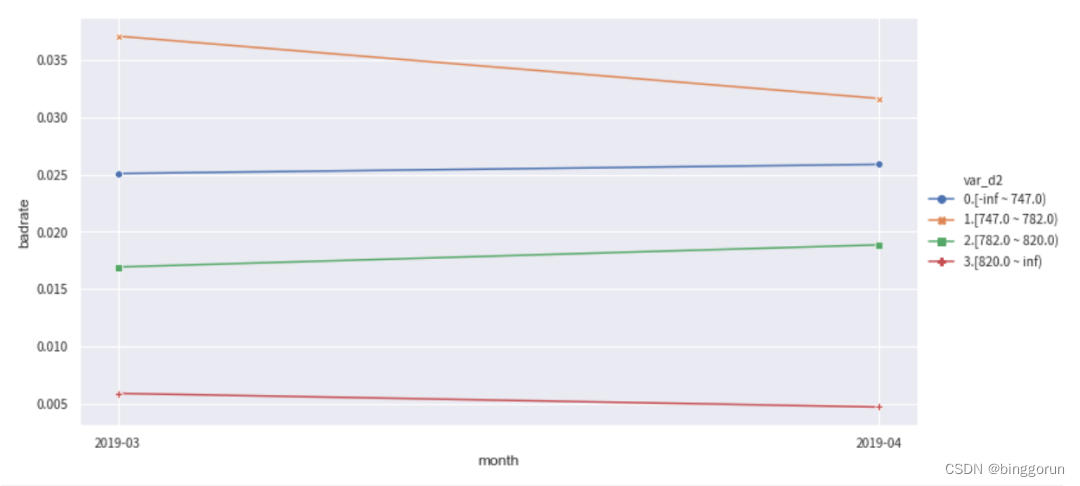
下面分别观察变量var_d2在训练集和oot测试集中随时间month变化的稳定性。正常情况下,每个分箱的bad_rate应该都有所区别,并且随时间保持稳定不交叉。如果折现有所交叉,说明分箱不稳定,需要重新调整。
from toad.plot import badrate_plot
col = 'var_d2'
# 观察 'var_d2' 分别在时间内和oot中的稳定性
badrate_plot(c.transform(train[[col,'target','month']], labels=true), target='target', x='month', by=col)
badrate_plot(c.transform(oot[[col,'target','month']], labels=true), target='target', x='month', by=col)
'''
敞口随时间变化而增大为优,代表了变量在更新的时间区分度更强。线之前没有交叉为优,代表分箱稳定。
'''
五、woe转化
woe转化在分箱调整好之后进行,步骤如下:
根据训练好的transer输出woe转化的数据,用于转化test/oot数据。
# 初始化
transer = toad.transform.woetransformer()
# combiner.transform() & transer.fit_transform() 转化训练数据,并去掉target列
train_woe = transer.fit_transform(c.transform(train_selected), train_selected['target'], exclude=to_drop+['target'])
oot_woe = transer.transform(c.transform(oot))
print(train_woe.head(3))
#结果输出:
'''
app_id_c target var_d2 var_d3 var_d5 var_d6 var_d7 \
0 app_1 0 -0.178286 0.046126 0.090613 0.047145 0.365305
1 app_2 0 -1.410248 0.046126 -0.271655 0.047145 -0.734699
2 app_3 0 -0.178286 0.046126 0.090613 0.047145 0.365305
var_d11 var_b3 var_b9 ... var_l_60 var_l_64 var_l_68 var_l_71 \
0 -0.152228 -0.141182 -0.237656 ... 0.132170 0.080656 0.091919 0.150975
1 -0.152228 0.199186 0.199186 ... 0.132170 0.080656 0.091919 0.150975
2 -0.152228 -0.141182 0.388957 ... -0.926987 -0.235316 -0.883896 -0.385976
var_l_89 var_l_91 var_l_107 var_l_119 var_l_123 month
0 0.091901 0.086402 -0.034434 0.027322 0.087378 2019-03
1 0.091901 0.086402 -0.034434 0.027322 0.087378 2019-03
2 0.091901 -0.620829 -0.034434 -0.806599 -0.731941 2019-03
[3 rows x 34 columns]
'''
六、逐步回归
toad.selection.stepwise
逐步回归特征筛选,支持向前,向后和双向。 逐步回归属于包裹式的特征筛选方法,这部分通过使用sklearn的ref实现。
根据多次验证,一般来讲 direction = 'both’效果最好。estimator = 'ols’以及criterion = 'aic’运行速度快且结果对逻辑回归建模有较好的代表性。
# 将woe转化后的数据做逐步回归
final_data = toad.selection.stepwise(train_woe,target = 'target', estimator='ols', direction = 'both', criterion = 'aic', exclude = to_drop)
# 将选出的变量应用于test/oot数据
final_oot = oot_woe[final_data.columns]
print(final_data.shape) # 逐步回归从31个变量中选出了10个
#结果输出:
'''
(43576, 13)
'''
#最后筛选后,再次确定建模要用的变量。
col = list(final_data.drop(to_drop+['target'],axis=1).columns)
七、建模和模型评估
首先,使用逻辑回归建模,通过sklearn实现。模型参数比如正则化、样本权重等不在这里详解。
用逻辑回归建模
# 用逻辑回归建模
from sklearn.linear_model import logisticregression
lr = logisticregression()
lr.fit(final_data[col], final_data['target'])
# 预测训练和隔月的oot
pred_train = lr.predict_proba(final_data[col])[:,1]
pred_oot_may =lr.predict_proba(final_oot.loc[final_oot.month == '2019-05',col])[:,1]
pred_oot_june =lr.predict_proba(final_oot.loc[final_oot.month == '2019-06',col])[:,1]
pred_oot_july =lr.predict_proba(final_oot.loc[final_oot.month == '2019-07',col])[:,1]
然后,计算模型预测结果。风控模型常用的评价指标有: ks、auc、psi等。下面展示如果通过toad快速实现完成。
ks 和 auc
评价指标
from toad.metrics import ks, auc
print('train ks',ks(pred_train, final_data['target']))
print('train auc',auc(pred_train, final_data['target']))
print('oot结果')
print('5月 ks',ks(pred_oot_may, final_oot.loc[final_oot.month == '2019-05','target']))
print('6月 ks',ks(pred_oot_june, final_oot.loc[final_oot.month == '2019-06','target']))
print('7月 ks',ks(pred_oot_july, final_oot.loc[final_oot.month == '2019-07','target']))
#结果输出:
'''
train ks 0.3707986228750539
train auc 0.75060723924743
'''
#oot结果
'''
5月 ks 0.3686687175756087
6月 ks 0.3495273403486497
7月 ks 0.3796914199845523
'''
psi
psi分为两种,一个是变量的psi,一个是模型的psi。
下面是变量psi的计算,比较训练集和oot的变量分布之间的差异。
toad.metrics.psi(final_data[col], final_oot[col])
#结果输出:
'''
var_d2 0.000254
var_d5 0.000012
var_d7 0.000079
var_d11 0.000191
var_b10 0.000209
var_b18 0.000026
var_b19 0.000049
var_b23 0.000037
var_l_20 0.000115
var_l_68 0.000213
dtype: float64
'''
模型psi的计算,分别计算训练集和oot模型预测结果的差异,下面细分为三个月份比较。
print(toad.metrics.psi(pred_train,pred_oot_may))
print(toad.metrics.psi(pred_train,pred_oot_june))
print(toad.metrics.psi(pred_train,pred_oot_june))
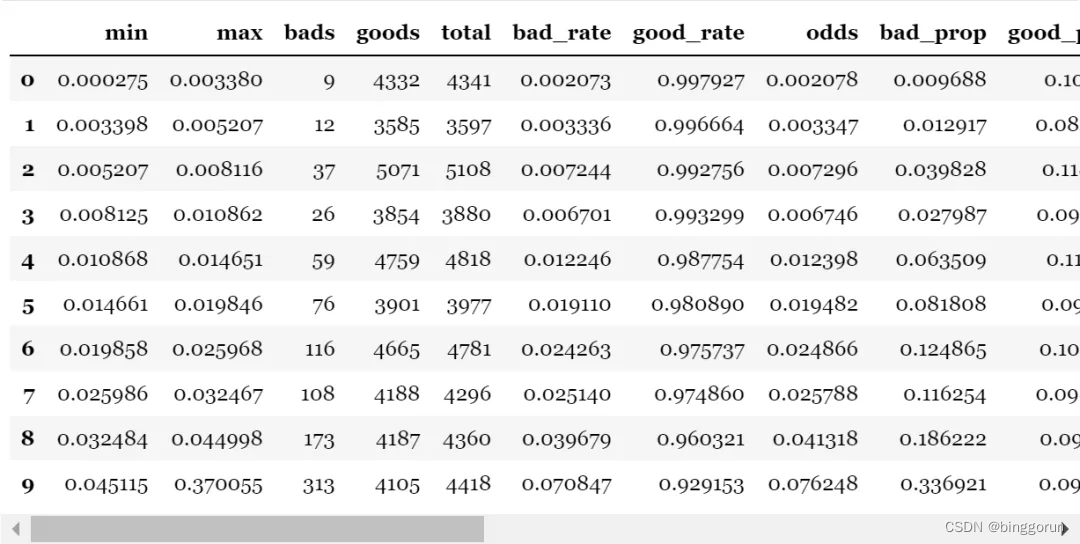
另外,toad还提供了整个评价指标的汇总,输出模型预测分箱后评判信息,包括每组的分数区间,样本量,坏账率,ks等。
toad.metrics.ks_bucket
- bad_rate为每组坏账率:
组之间的坏账率差距越大越好
可以用于观察是否有跳点
可以用与找最佳切点
可以对比
# 将预测等频分箱,观测每组的区别
toad.metrics.ks_bucket(pred_train, final_data['target'], bucket=10, method = 'quantile')
八、转换评分
toad.scorecard
最后一步就是将逻辑回归模型转标准评分卡,支持传入逻辑回归参数,进行调参。
结果输出:
'''
scorecard(base_odds=35, base_score=750, card=none,
combiner=<toad.transform.combiner object at 0x1a2434fdd8>, pdo=60,
rate=2,
transer=<toad.transform.woetransformer object at 0x1a235a5358>)
'''
注:评分卡在 fit 时使用 woe 转换后的数据来计算最终的分数,分数一旦计算完成,便无需 woe 值,可以直接使用 原始数据 进行评分。
# 直接使用原始数据进行评分
card.predict(train)
#输出标准评分卡
card.export()
#结果输出:
{'var_d2': {'[-inf ~ 747.0)': 65.54,
'[747.0 ~ 782.0)': 45.72,
'[782.0 ~ 820.0)': 88.88,
'[820.0 ~ inf)': 168.3},
'var_d5': {'o,nan': 185.9, 'f': 103.26, 'm': 68.76},
'var_d7': {'large fleet operator,company,strategic transprter,salaried,housewife': 120.82,
'doctor-self employed,nan,sal(retiral age 60),services,sal(retiral age 58),others,doctor-salaried,agent,consultant,director,medium fleetoperator,trader,retail transporter,manufacturing,first time users,student,pensioner': 81.32,
'proprietor,trading,strategic captive,self-employed,serv-private sector,small rd trans.opr,businessman,caretaker,retail,agriculturist,retired personnel,manager,contractor,accountant,banks service,government service,advisor,strategic s1,schools,teacher,genaral retailer,restaurant keeper,officer,policeman,serv-public sector,barrister,salaried,salesman,retail captive,defence (nco),strategic s2,others not defined,jeweller,secretary,sup strat transport,lecturer,attorney at law,tailor,technician,clerk,planter,driver,priest,programmer,executive assistant,proof reader,stockbroker(s)-commd,typist,adminstrator,industry,pharmacist,trading,taxi driver,strategic bus op,chairman,carpenter,dispenser,helper,strategic s3,retail bus operator,garagist,private tailor,nurse': 55.79},
'var_d11': {'n': 88.69, 'u': 23.72},
'var_b10': {'[-inf ~ -8888.0)': 67.76,
'[-8888.0 ~ 0.548229531)': 97.51,
'[0.548229531 ~ inf)': 36.22},
'var_b18': {'[-inf ~ 2)': 83.72, '[2 ~ inf)': 39.23},
'var_b19': {'[-inf ~ -9999)': 70.78, '[-9999 ~ 4)': 97.51, '[4 ~ inf)': 42.2},
'var_b23': {'[-inf ~ -8888)': 64.51, '[-8888 ~ inf)': 102.69},
'var_l_20': {'[-inf ~ 0.000404297)': 78.55,
'[0.000404297 ~ 0.003092244)': 103.85,
'[0.003092244 ~ inf)': 36.21},
'var_l_68': {'[-inf ~ 0.000255689)': 70.63,
'[0.000255689 ~ 0.002045513)': 24.56,
'[0.002045513 ~ 0.007414983000000002)': 66.63,
'[0.007414983000000002 ~ 0.019943748)': 99.55,
'[0.019943748 ~ inf)': 142.36}
}
九、其他功能
toad.transform.gbdttransformer
toad还支持用gbdt编码,用于gbdt + lr建模的前置。这种融合的方式来自facebook,即先使用gbdt训练输出,再将输出结果作为lr的输入训练,以此达到更好的学习效果。
gbdt_transer = toad.transform.gbdttransformer()
gbdt_transer.fit(final_data[col+['target']], 'target', n_estimators = 10, max_depth = 2)
gbdt_vars = gbdt_transer.transform(final_data[col])
gbdt_vars.shape
#>> (43576, 40)
以上就是toad的基本用法。
与其他模型的比较
lr与svn比较
相同点
1)lr和svm都是分类算法。
2)如果不考虑核函数,lr和svm都是线性分类算法,也就是说他们的分类决策面都是线性的。
3)lr和svm都是监督学习算法。
4)lr和svm都是判别模型。
区别
1)lr和svm的不同,本质上是其loss function不同。逻辑回归方法基于概率理论,假设样本为1的概率可以用sigmoid函数来表示,然后通过极大似然估计的方法估计出参数的值;支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面。
2)支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用)。影响svm决策面的样本点只有少数的结构支持向量,当在支持向量外添加或减少任何样本点对分类决策面没有任何影响;而在lr中,每个样本点都会影响决策面的结果。
3)在解决非线性问题时,支持向量机采用核函数的机制,而lr通常不采用核函数的方法(lr里运用核函数的原理,带来的计算复杂度很高)
4)线性svm依赖数据表达的距离测度,所以需要对数据先做normalization,lr不受其影响;
5)svm的损失函数就自带正则(损失函数中的1/2||w||^2项),这就是为什么svm是结构风险最小化算法的原因;而lr必须另外在损失函数上添加正则项


发表评论