🔥前言

冒泡排序算法的基本思想是通过重复遍历待排序的数列,比较每对相邻元素,如果它们的顺序错误(根据元素排序规则来说)就把它们交换过来。这个过程中,较小的元素会像气泡一样逐渐“浮”到数列的顶端,也就是数列的前端。这个过程会重复进行,直到数列被排序完成
🚀冒泡排序python实现
算法实现
def bubble_sort(arr):
n = len(arr)
# 遍历所有数组元素
for i in range(n):
# last i elements are already in place
for j in range(0, n-i-1):
# 遍历数组从0到n-i-1
# 交换如果元素大于下一个元素
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
图形化算法展示
代码如下:
import matplotlib.pyplot as plt
def bubble_sort(arr):
n = len(arr)
plt.ion() # 开启交互模式
for i in range(n):
for j in range(1, n-i):
if arr[j-1] > arr[j]:
arr[j-1], arr[j] = arr[j], arr[j-1] # 交换元素
plt.clf() # 清除之前的图形
plt.plot(arr, 'ro-') # 绘制当前数组状态
plt.title('bubble sort animation')
plt.draw() # 绘制更新
plt.pause(1) # 暂停一段时间,以便观察
# 创建一个待排序的数组
arr = [64, 34, 25, 12, 22, 11, 90]
# arr = []
# num = int(input("请输入需要排序的数字个数:"))
# print("请依次输入需要排序的数字\n")
# for i in range(num):
# arr.append(int(input(f"第{i+1}个数:")))
# print("原始数组:")
# print(arr)
#
# bubble_sort(arr)
# print("排序后的数组:")
# print(arr)
# 原始数组的图形绘制
plt.figure(figsize=(10, 5))
plt.plot(arr, 'ro-', markersize=8)
plt.title('original data')
plt.grid(true)
plt.show()
plt.ioff()
# 开始冒泡排序并动态绘制
bubble_sort(arr.copy()) # 使用数组的副本以保留原始数组用于比较
# 排序后的数组图形绘制
plt.plot(arr, 'go-', markersize=8) # 使用绿色表示排序后的数组
plt.title('sorting raw data')
plt.grid(true)
plt.show()
plt.ioff() # 关闭图形交互模式
图形显示结果:
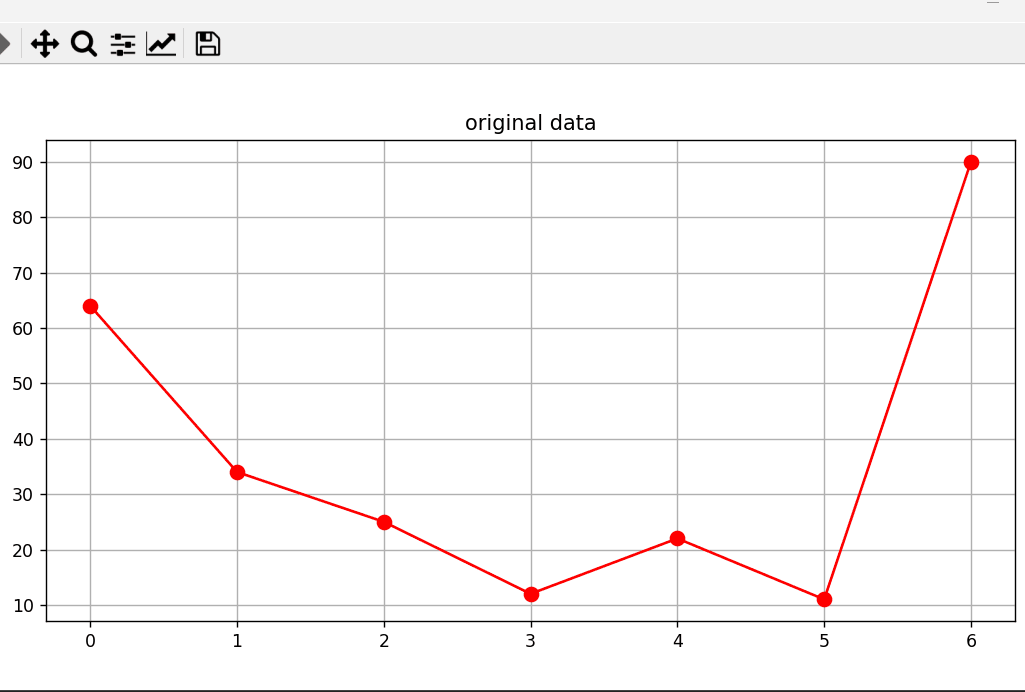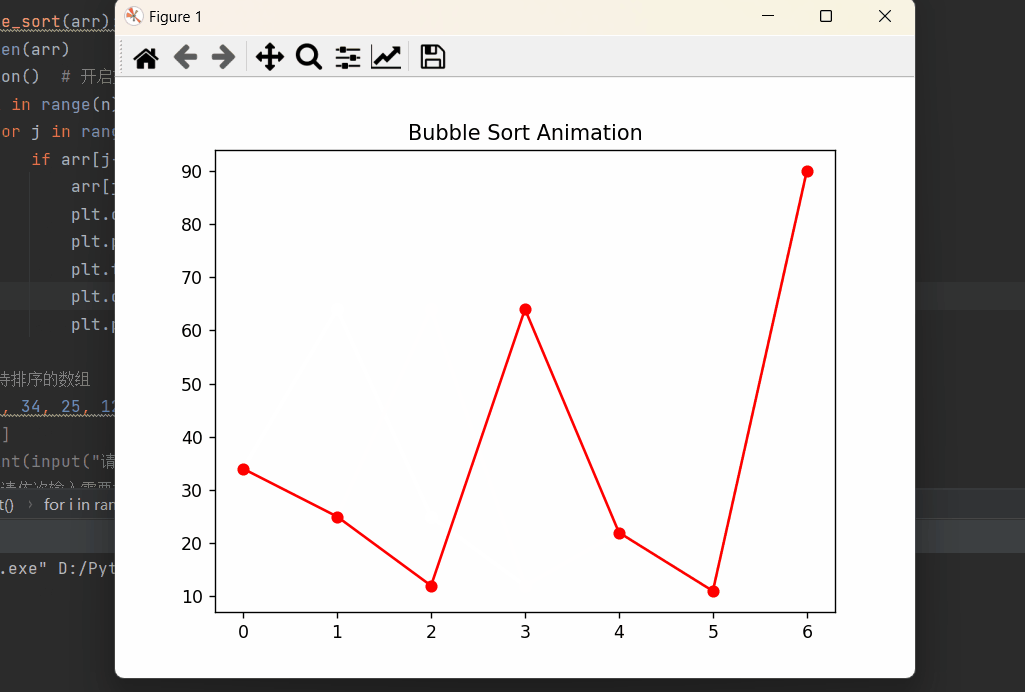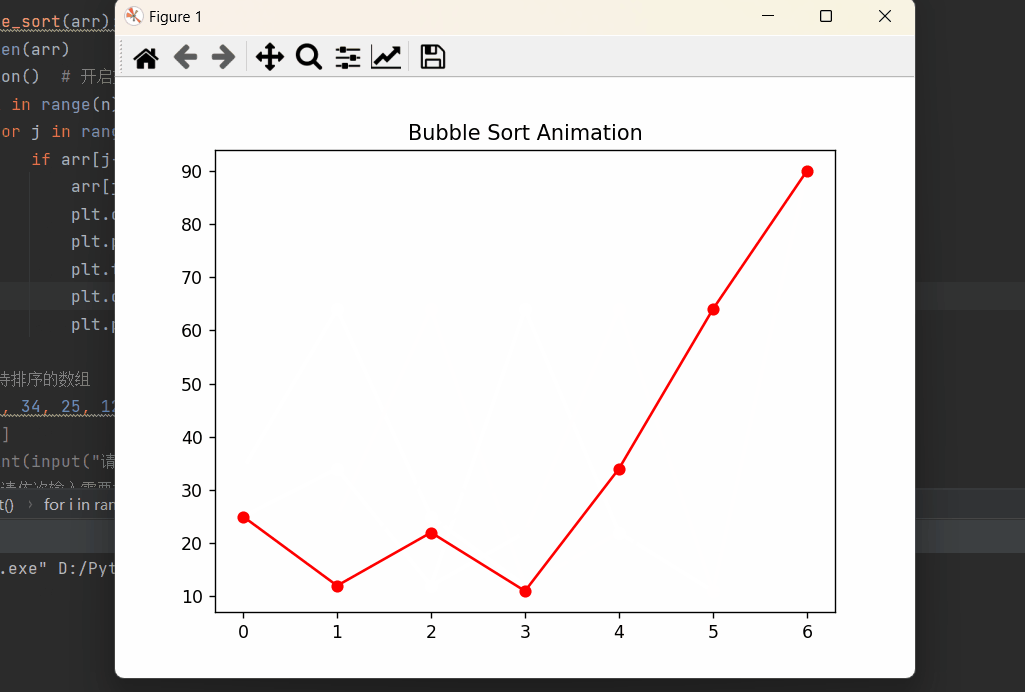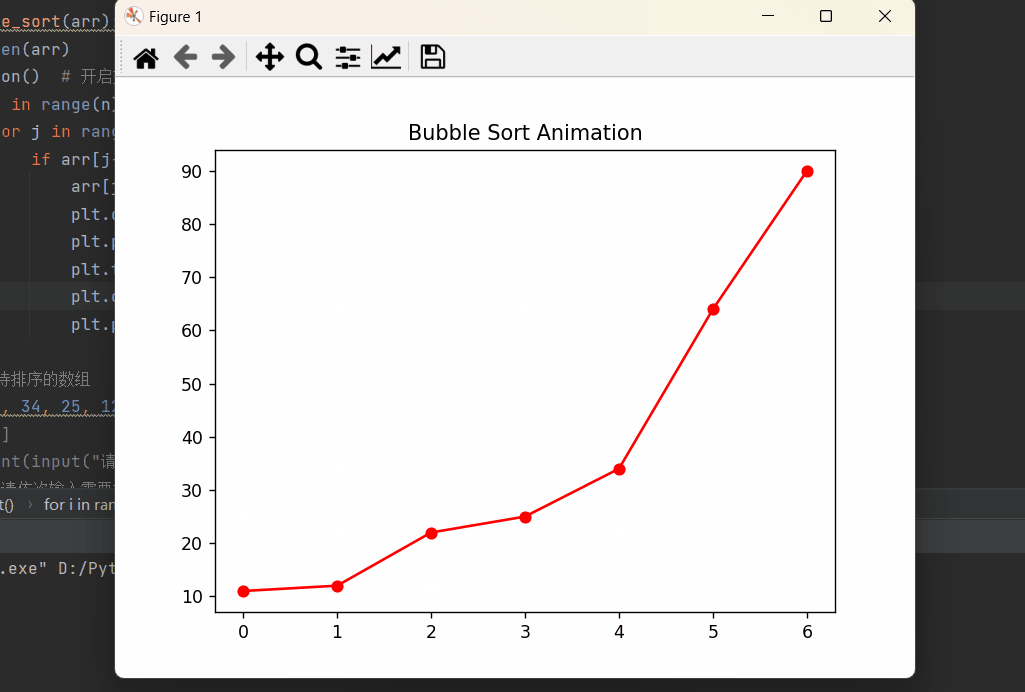
⭐️⭐️⭐️总结
冒泡排序(bubble sort)是一种简单直观的排序算法,它通过重复遍历待排序的数列,比较每对相邻元素的大小,并在必要时交换它们的位置。以下是冒泡排序的几个关键点总结:
1️⃣算法原理:
通过相邻元素的比较和交换,使得每一轮遍历后,数列中的最大(或最小)元素“冒泡”到它应该在的位置。
2️⃣稳定性:
冒泡排序是一种稳定的排序算法,因为它不会改变相同元素之间的相对顺序。
3️⃣时间复杂度:
最好情况(已经是排序状态):o(n),只需要遍历一次就发现没有元素交换,立即结束。
最坏情况(完全逆序):o(n^2),需要进行n-1次遍历。
平均情况:o(n^2)。
4️⃣空间复杂度:
空间复杂度为o(1),因为它是一种原地排序算法,不需要额外的存储空间。
实现方式:
可以使用两次嵌套循环实现,外层循环控制遍历次数,内层循环进行相邻元素的比较和交换。


发表评论