目录
初识svm算法
支持向量机(support vector machine,svm)是一种经典的监督学习算法,用于解决二分类和多分类问题。其核心思想是通过在特征空间中找到一个最优的超平面来进行分类,并且间隔最大。
svm能够执行线性或非线性分类、回归,甚至是异常值检测任务。它是机器学习领域最受欢迎的模型之一。svm特别适用于中小型复杂数据集的分类。
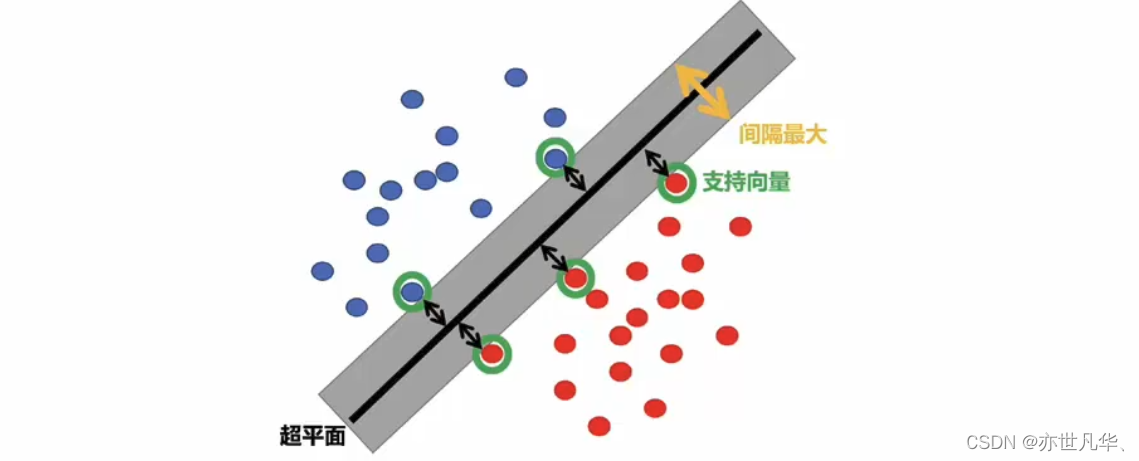
超平面最大间隔介绍:下左图显示了三种可能的线性分类器的决策边界;右图中的实线代表svm分类器的决策边界,不仅分离了两个类别,且尽可能远离最近的训练实例。
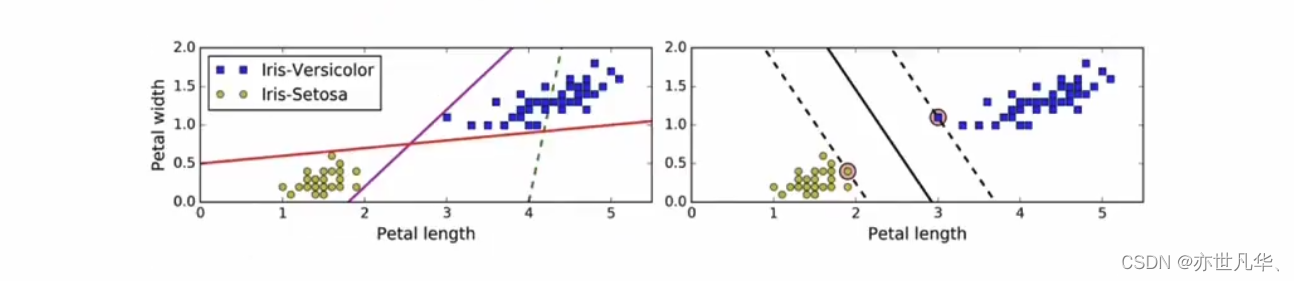
虚线所代表的模型表现非常糟糕,甚至都无法正确实现分类。其余两个模型在这个训练集上表现堪称完美,但是它们的决策边界与实例过于接近,导致在面对新实例时,表现可能不会太好。
硬间隔和软间隔:
接下来通过一个具体的案例来实现svm算法,这段代码使用了scikit-learn库中的支持向量机(support vector machine,svm)实现来进行分类任务:
from sklearn import svm
x = [[0, 0], [1, 1]]
y = [0, 1]
ss = svm.svc()
ss.fit(x, y)
result = ss.predict([[2, 2]])
print(result)通过拟合得到一个最优的超平面来进行二分类任务,然后使用训练好的模型对新样本进行分类预测,并将预测结果打印出来:

svm算法原理
svm通过优化一个凸二次规划问题来求解最佳的超平面,其中包括最小化模型的复杂度(即最小化权重的平方和),同时限制训练样本的误分类情况。这个优化问题可以使用拉格朗日乘子法来求解。对于非线性可分的情况,svm可以通过核函数(kernel function)将输入特征映射到高维空间,使得原本线性不可分的数据在高维空间中变得线性可分。常用的核函数包括线性核、多项式核、高斯核等。
假设给定一个特征空间上的训练集为:


以上就是线性可分支持向量机的模型表达式。我们要去求出这样一个模型,或者说这样一个超平面y(x),它能够最优地分离两个集合。
其实也就是我们要去求一组参数(w,b),使其构建的超平面函数能够最优地分离两个集合。如下就是一个最优超平面:
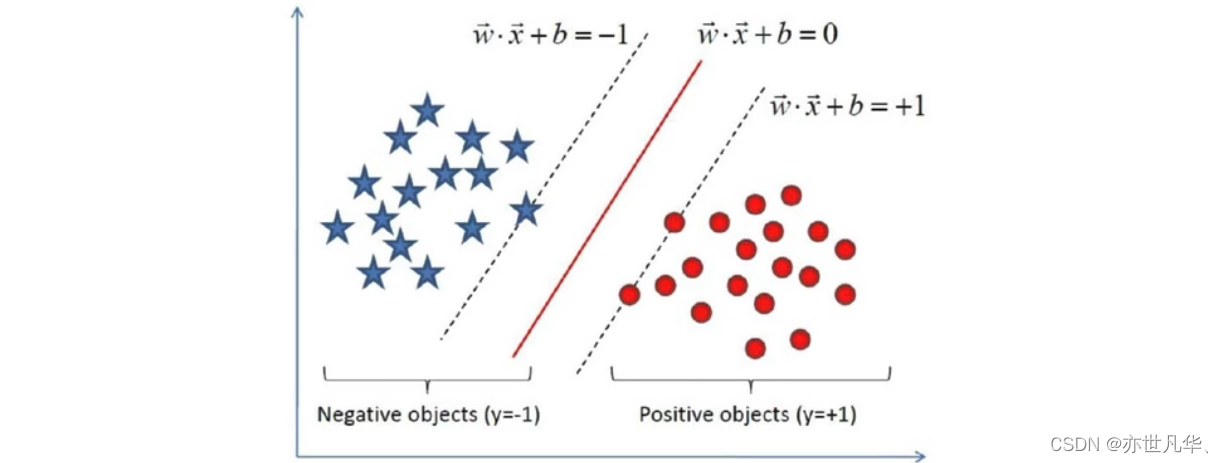
再比如下图的阴影部分是一个“过渡带”,“过渡带”的边界是集合中离超平面最近的样本点落在的地方:
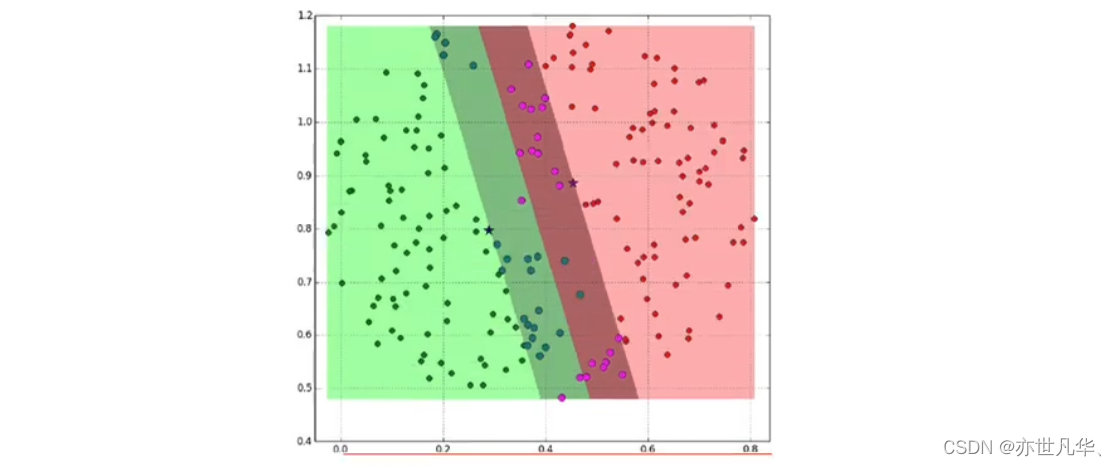
svm回归:让尽可能多的实例位于预测线上,同时限制间隔违例(也就是不在预测线距上的实例)。线距的宽度由超参数e控制:
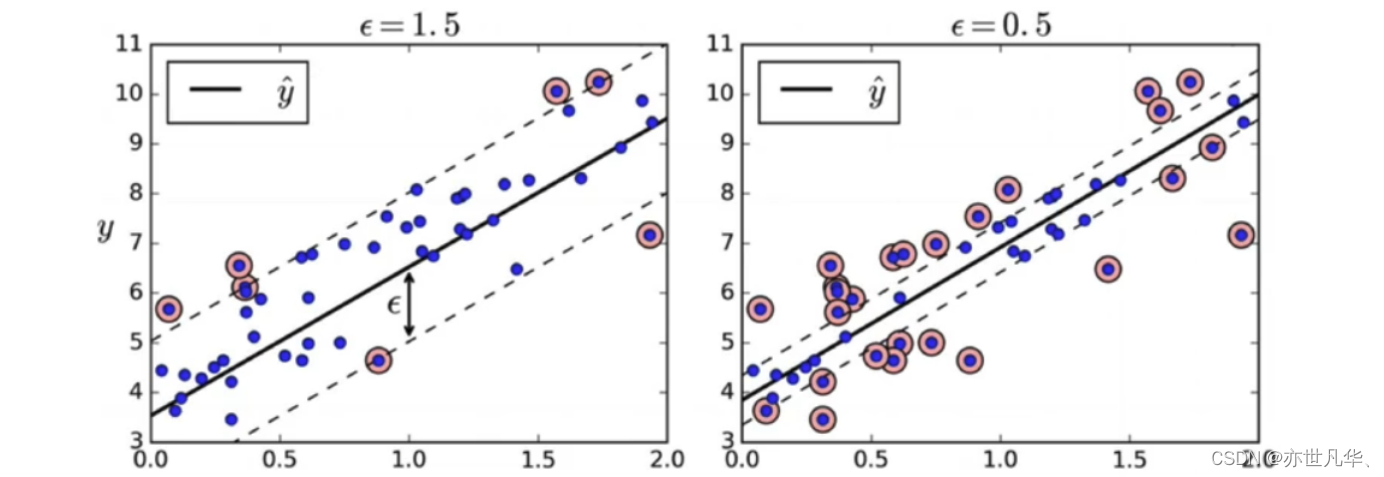
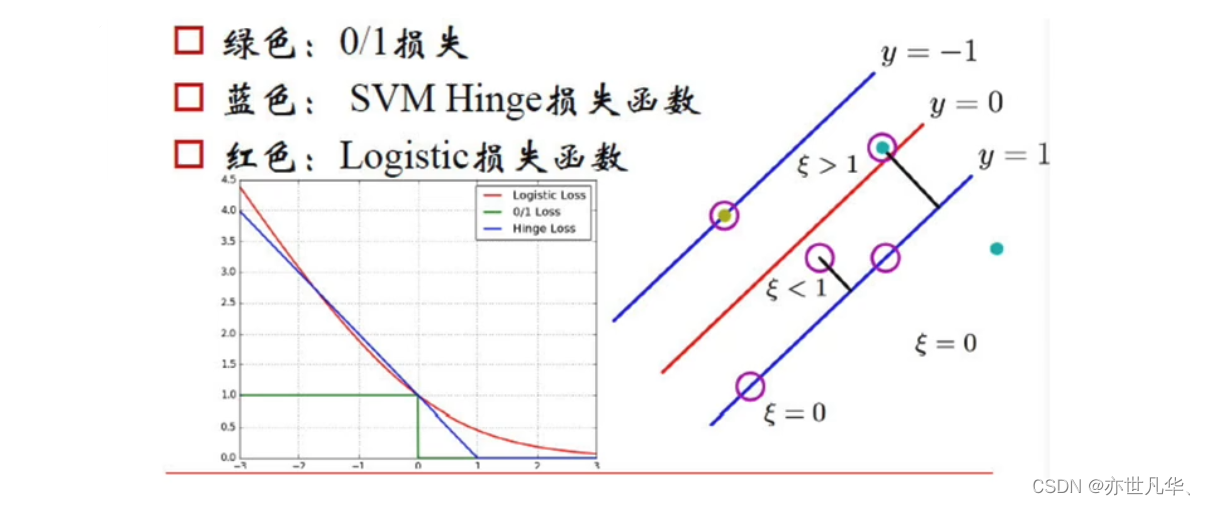
svm损失函数
支持向量机(svm)在分类问题中使用的损失函数是"hinge loss"(铰链损失),它通常被用于最大间隔分类,即寻找能够最大化分类间隔的超平面。而在svm中,我们主要讨论三种损失函数:
svm的核方法
核函数:是将原始输入空间映射到新的特征空间,从而,使得原本线性不可分的样本可能在核空间可分。核函数并不是svm特有的,核函数可以和其他算法也进行结合,只是核函数与svm结合的优势非常大。
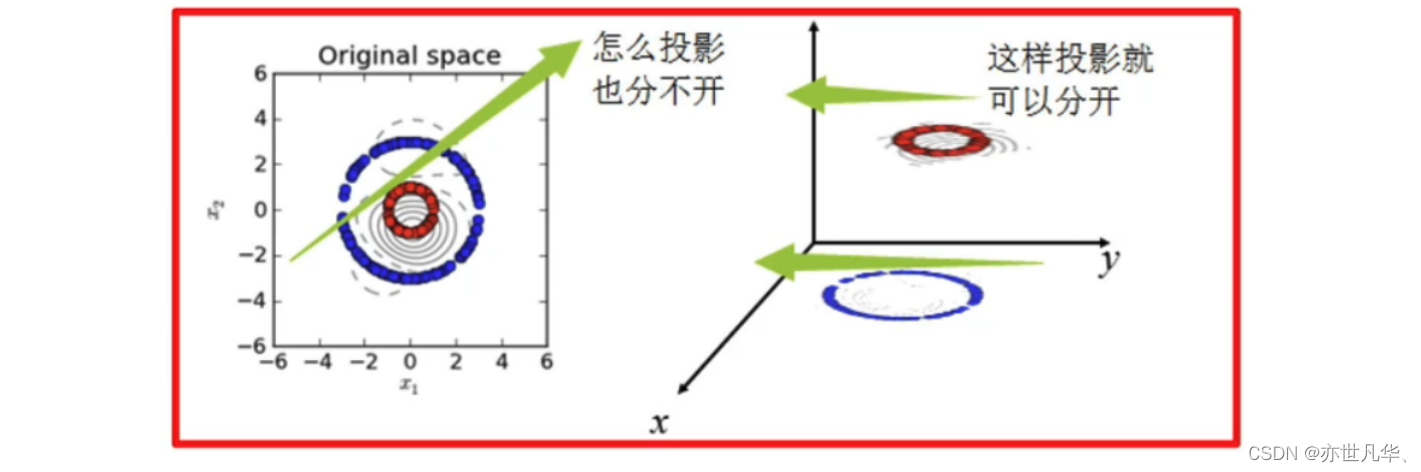
下图所示的两类数据,分别分布为两个圆圈的形状,这样的数据本身就是线性不可分的,此时我们就要思考该如何把这两类数据分开:
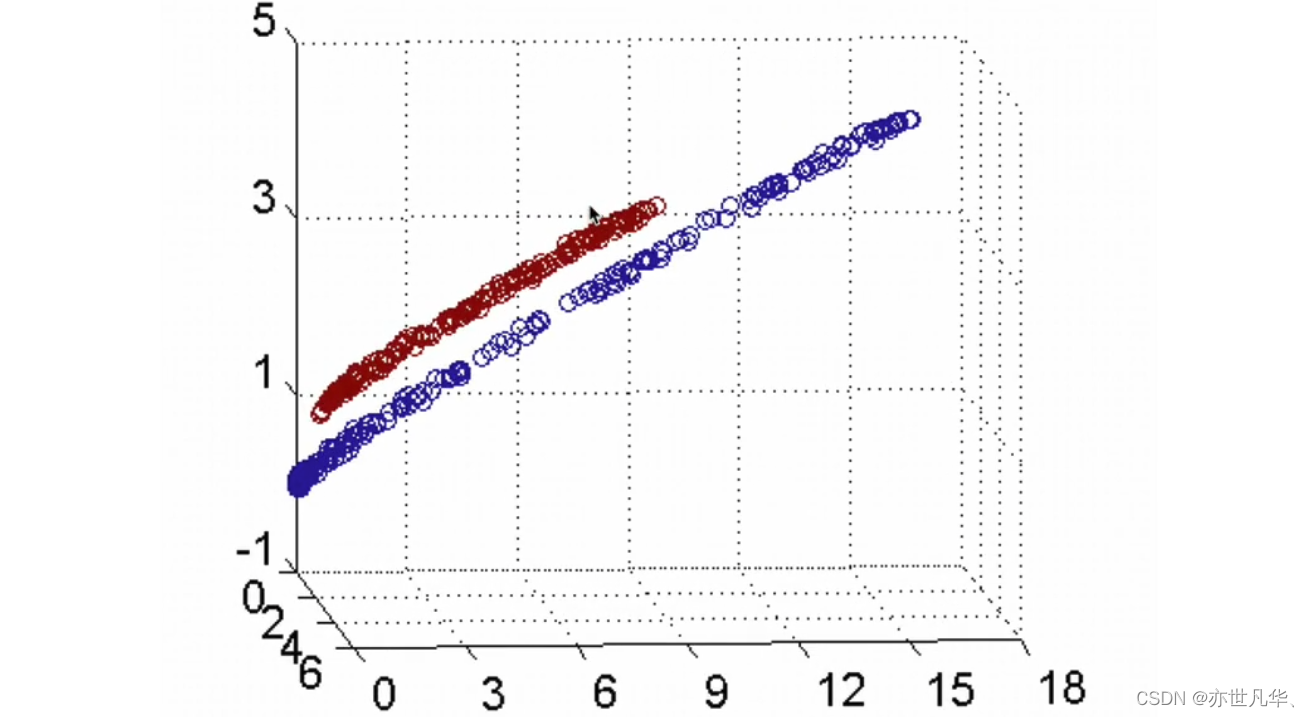

接下来通过核方法进行举例说明:
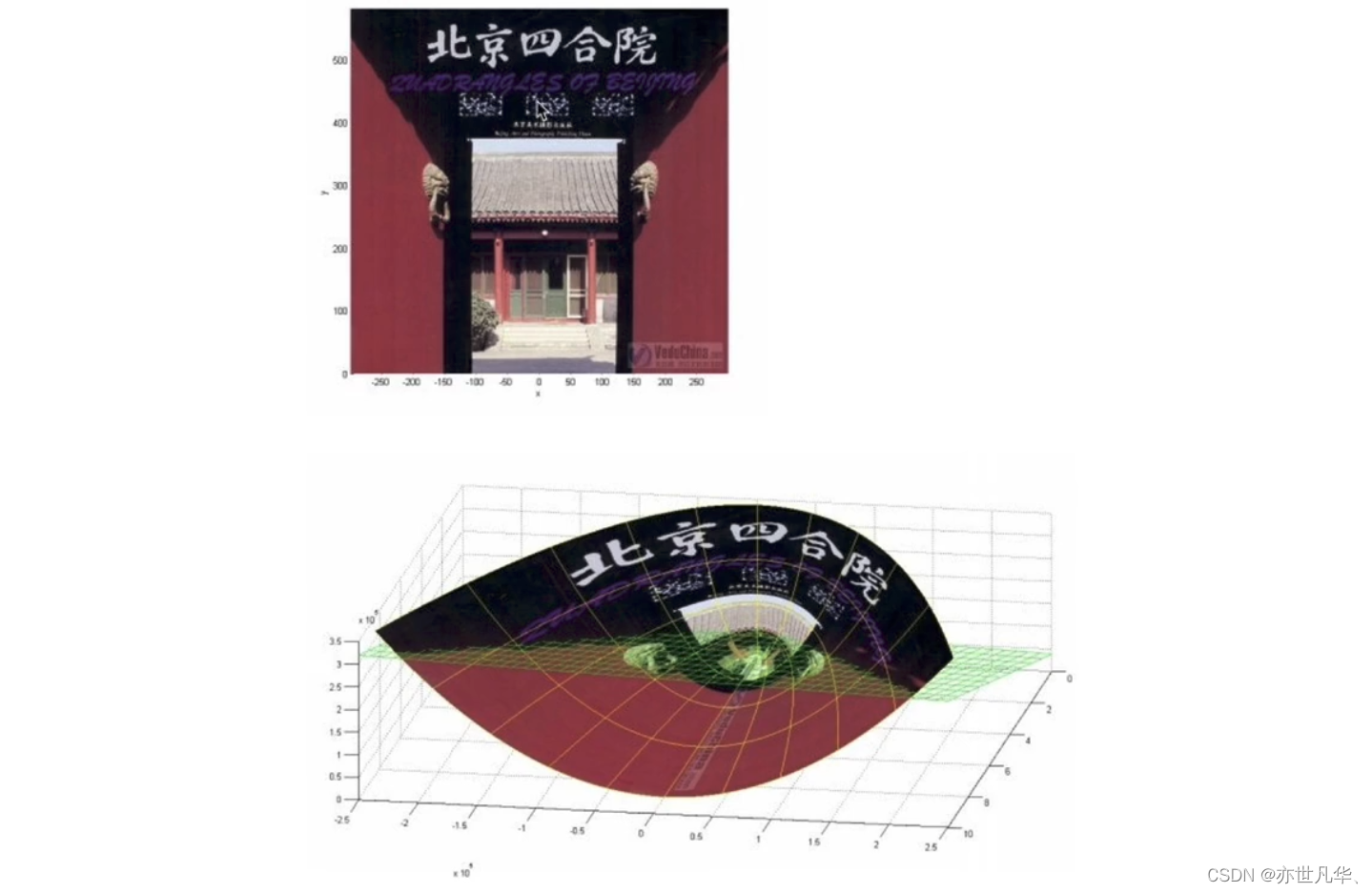
核函数的作用:一个从低维空间到高维空间的映射,而这个映射可以把低维空间中线性不可分的两类点变成线性可分的。

常见核函数:

总之,都是在定义距离,大于该距离,判为正,小于该距离,判为负。至于选择哪一种核函数,要根据具体的样本分布情况来确定,以下是使用的指导规则:
数字识别器(实操)
mnist(“修改后的国家标准与技术研究所")是计算机视觉事实上的"helloworld"数据集。自1999年发布以来,这一经典的手写图像数据集已成为分类算法基准测试的基础。随着新的机器学习技术的出现,mnist仍然是研究人员和学习者的可靠资源。
本次 案例 中,我们的目标是从数万个手写图像的数据集中正确识别数字:
训练集中的每个像素列都具有像pixelx这样的名称,其中x是0到783之间的整数,包括0和783。为了在图像上定位该像素,假设我们已经将x分解为×=i*28+j,其中i和j是0到27之间的整数,包括0和27。然后,pixelx位于28x28矩阵的第i行和第j列上(索引为零)。
例如,pixel31表示从左边开始的第四列中的像素,以及从顶部开始的第二行,如下面的asci图中所示。在视觉上,如果我们省略“像素”前缀,像素组成图像如下:
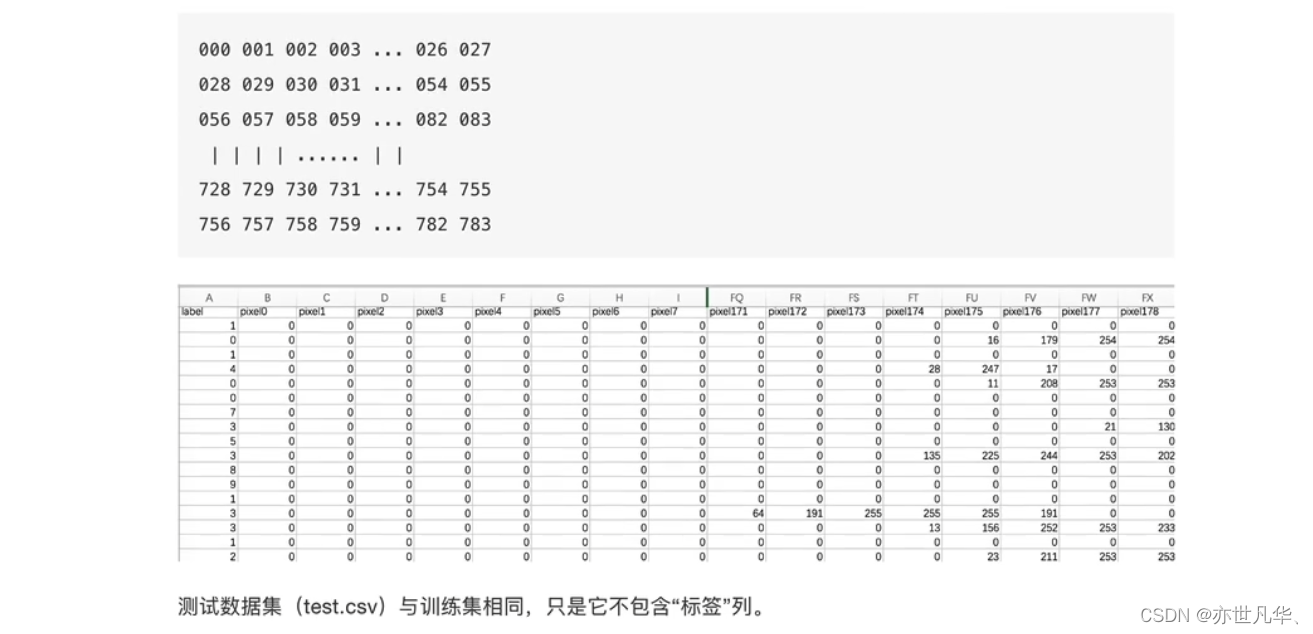
以下是案例实现的具体过程:
获取数据:
导入相关要使用的第三方库,获取数据集当中的数据:
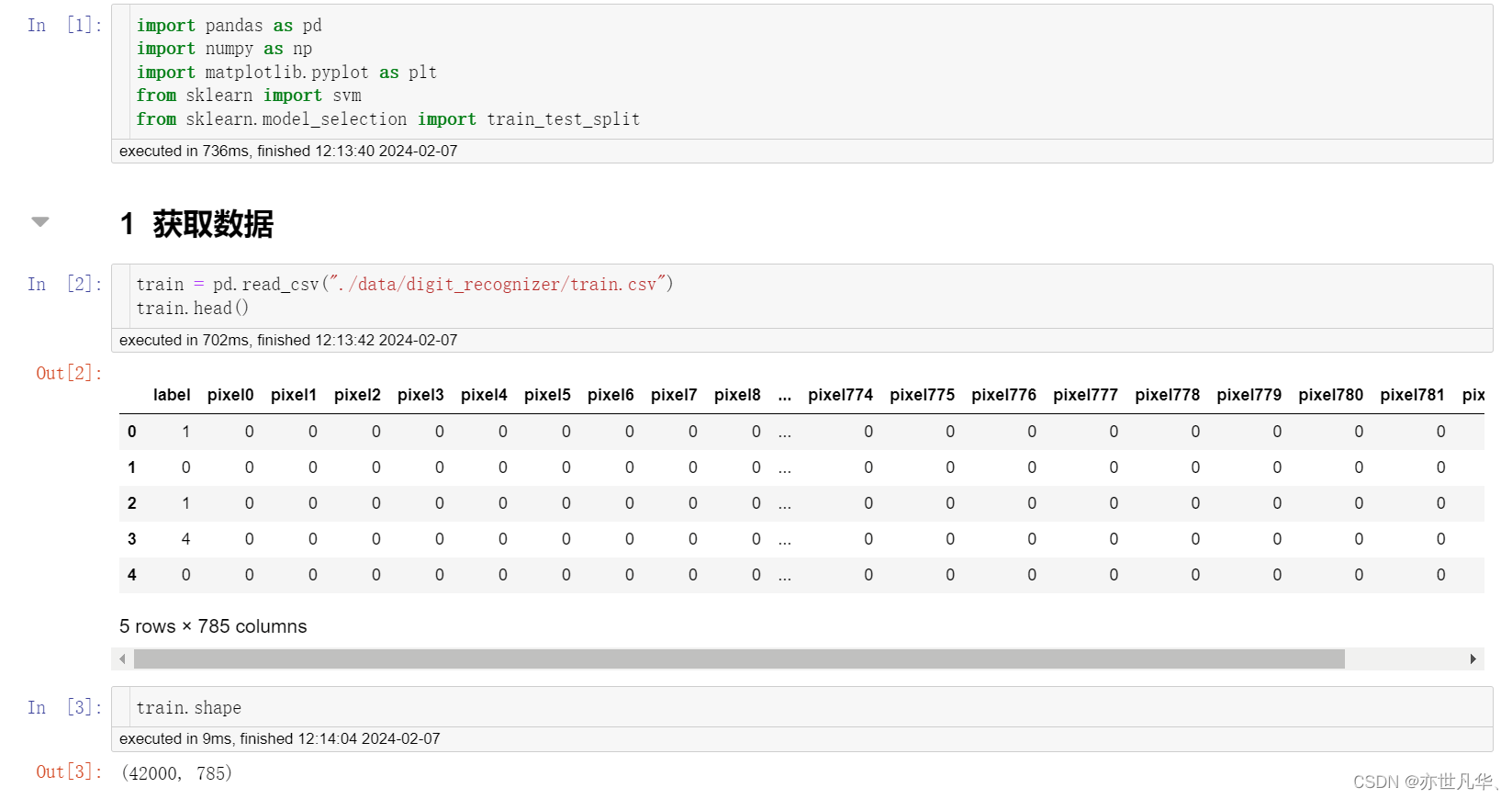
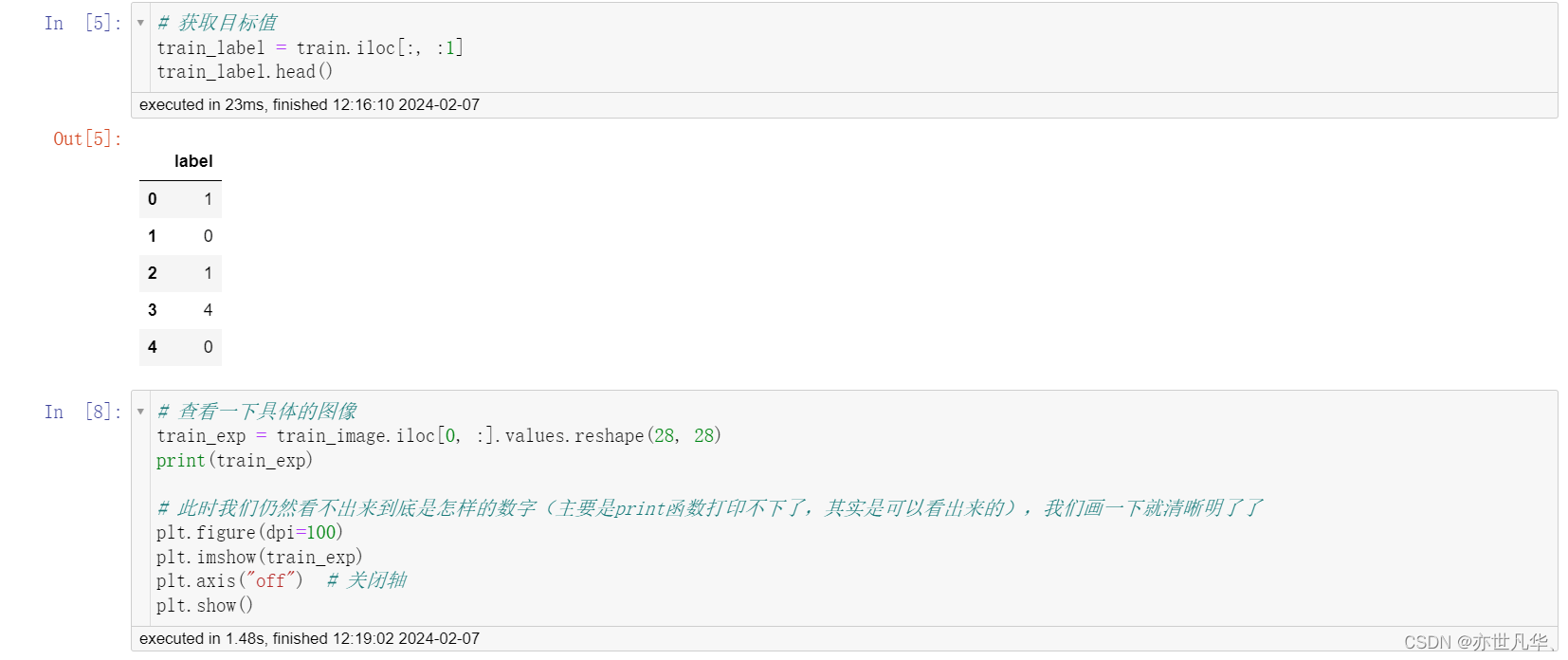
这里展示了图片资源给出的画面:
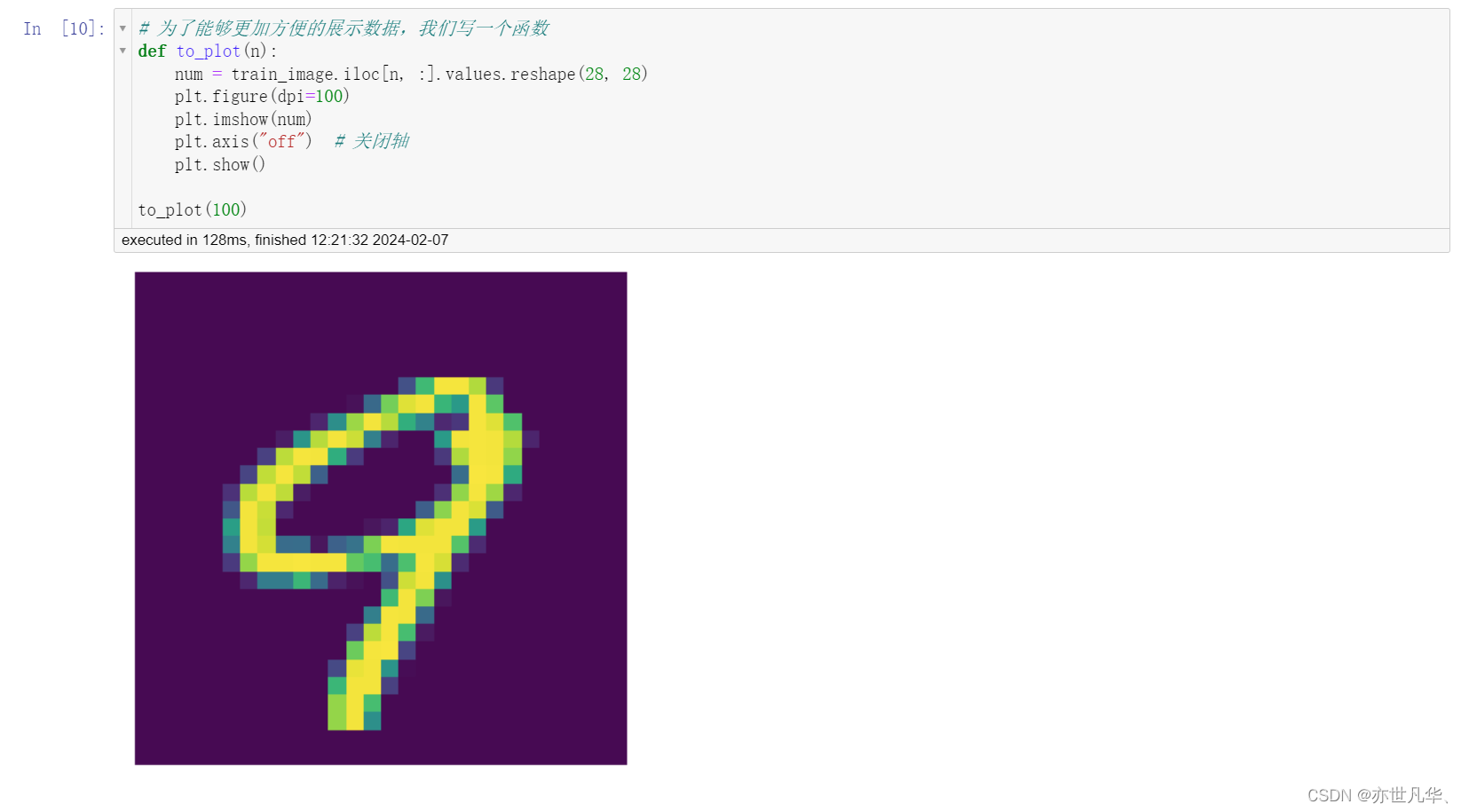
数据基本处理:
接下来给图片数据进行归一化处理:
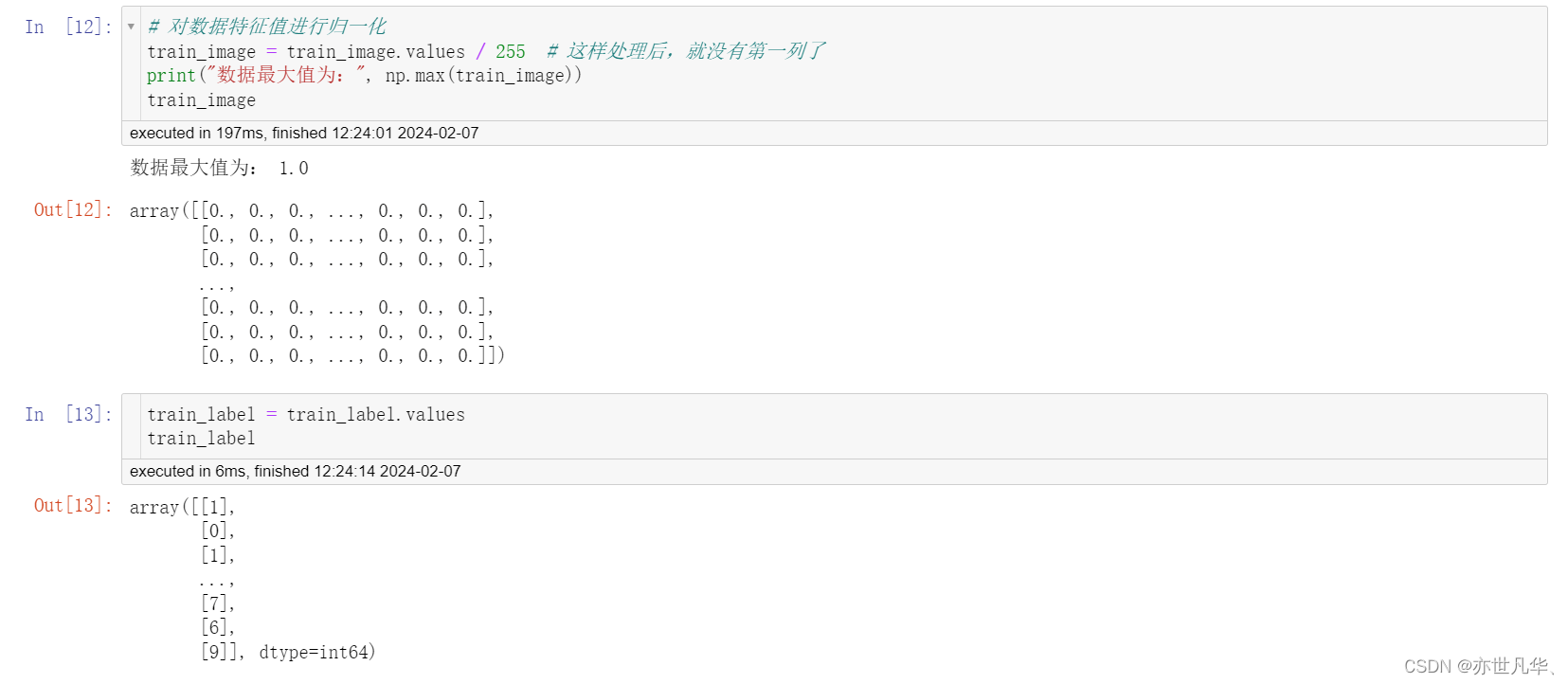
然后进行数据分割:
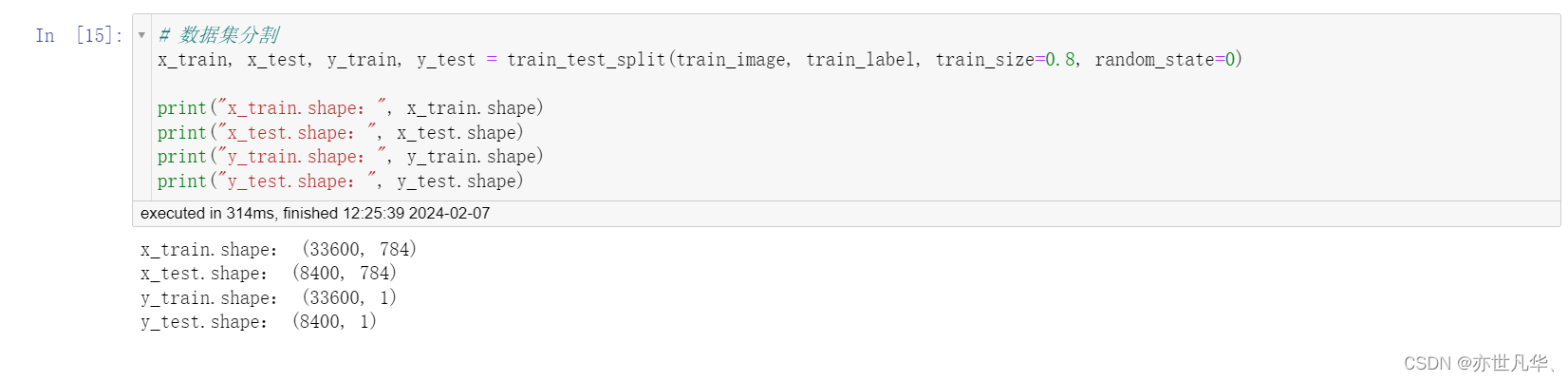
特征降维和模型优化:
这里进行数据的特征工程:
# 3. 特征降维和模型训练
import time
from sklearn.decomposition import pca
# 通过多次使用 pca 确定最优模型
def n_components_analysis(n, x_train, y_train, x_test, y_test):
# 记录开始时间
start= time.time()
# pca降维实现
pca = pca(n_components=n)
print("特征降维传递的参数为:{}".format(n))
pca.fit(x_train) # 学习如何降维
# 在训练集和测试集进行降维
x_train_pca = pca.transform(x_train)
x_test_pca = pca.transform(x_test)
# 利用 svm 进行模型训练(这里使用常见的svc)
print("开始使用svc进行训练")
svc = svm.svc()
svc.fit(x_train_pca, y_train.ravel())
# 获取accuracy结果
acc = svc.score(x_test_pca, y_test)
# 记录结束时间
end = time.time()
print(f"[n_components={n}]准确率为:{acc * 100:.4f}%,耗时{end - start:.2f}s\r\n")
return acc传递多个数值找到最合理的模型参数:
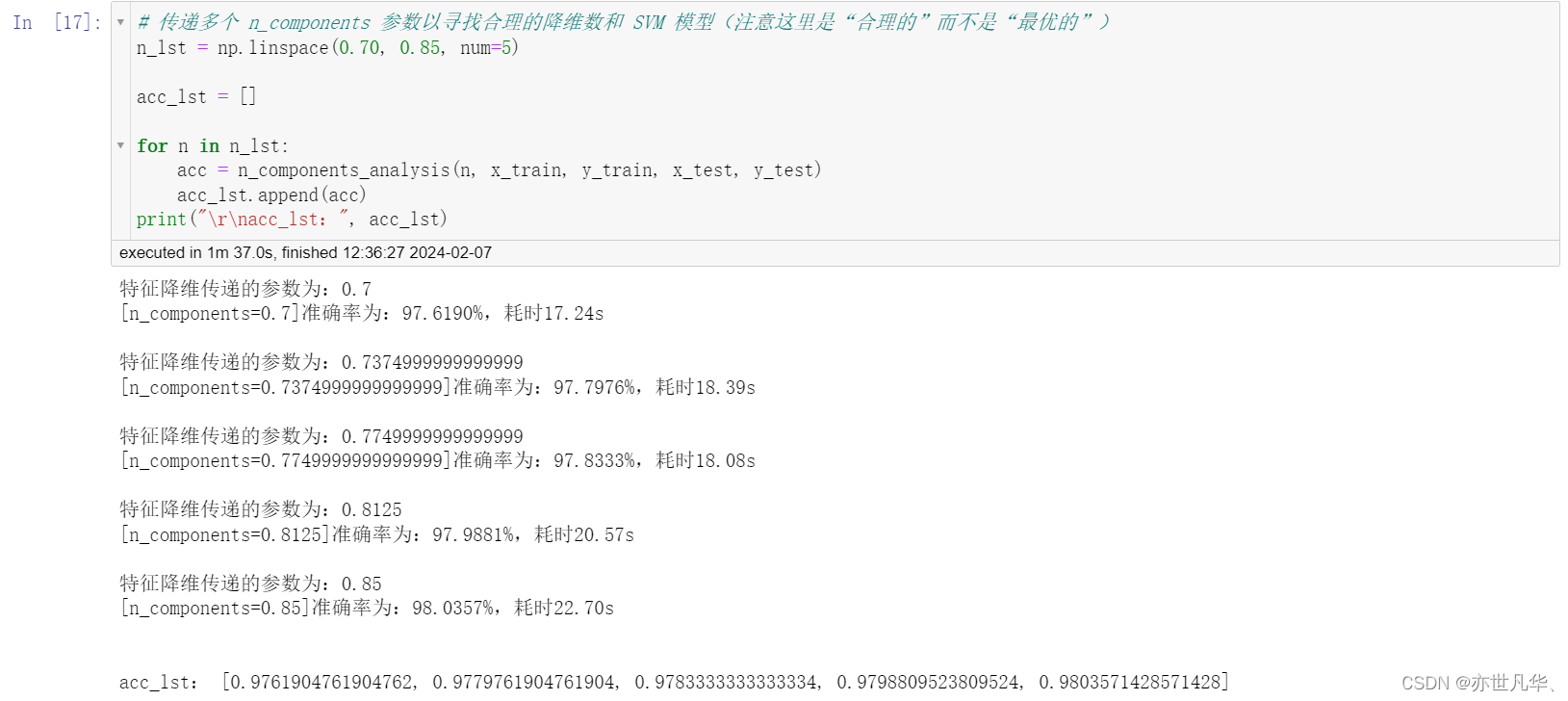
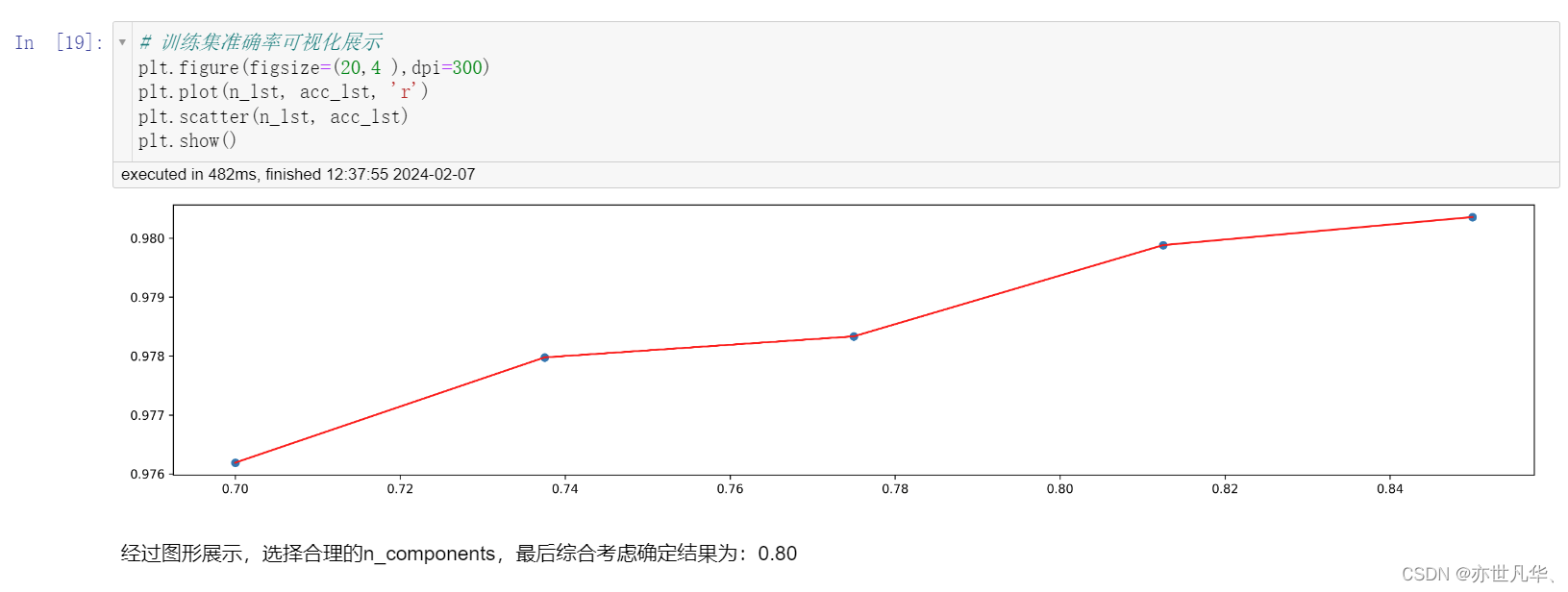
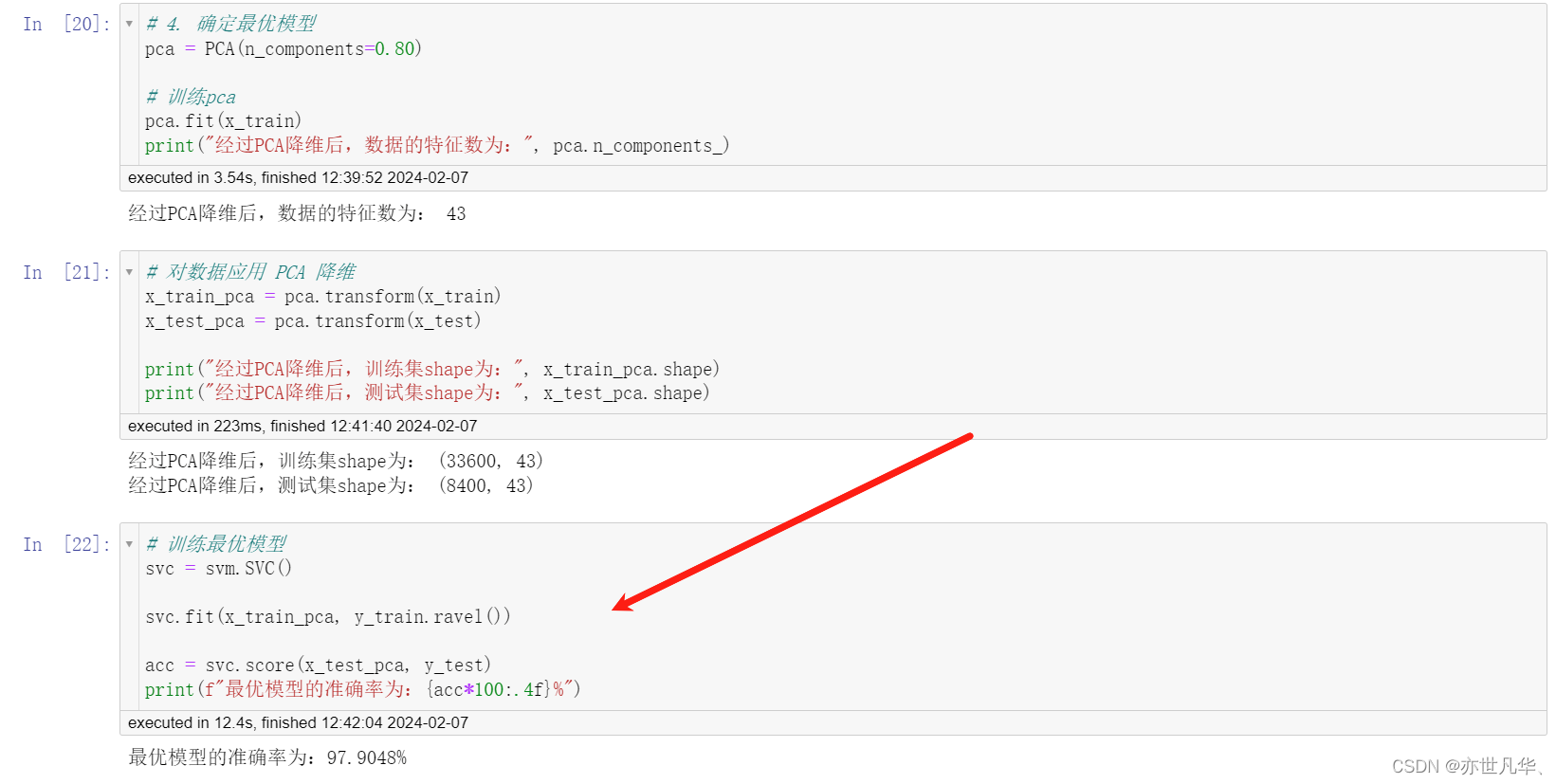
确定最优模型:



![[iOS]高版本MacOS运行低版本Xcode](https://images.3wcode.com/3wcode/20240728/s_0_202407282139442857.png)

发表评论