周五刮台风,实在不想上班,总结学习一下吧。因为我主要做图形学算法研究,图像算法的目标我就是会用能用就行,所以原理解释得不清晰,请见谅。
主要是项目做得一个检测,主要思路是用canny边缘检测目标,然后dbscan聚类目标,最后再根据点画最小包围框。目前网络上有dbscan的代码实现,但都是从文本读入点数据的,给萌新可能带来了不小的困扰。
做canny边缘检测先将rgb图变为灰度图,然后canny函数可以用opencv自带的,也可以自己写一个,自带的canny函数如下
void canny(inputarray image, outputarray edges, double threshold1, double threshold2, int aperturesize=3, bool l2gradient=false)第一个参数:inputarray类型的image,输入图像,需为单通道8位图像。
第二个参数:outputarray类型的edges,输出的边缘图,需要和输入图像有相同的尺寸和类型。
第三个参数:double类型的threshold1,第一个滞后性阈值。
第四个参数:double类型的threshold2,第二个滞后性阈值。
第五个参数:int类型的aperturesize,表示sobel算子的孔径的大小,默认值时3.
第六个参数:bool类型的l2gradient,一个计算图像梯度复制的标识,默认false。
这样子看还是无法理解这些参数到底是干啥的,所以详细学习一下canny的过程
step1:高斯滤波平滑图像,会让图像变模糊,但是可以减少图像中噪声。高斯滤波一般核大小为5*5,高斯滤波核如何获得可以参考这篇大佬的文章
step2:使用sobel算子计算像素梯度,sobel算子是两个 3×3 的矩阵,分别为 sx和 sy。前者用于计算图像 x 方向像素梯度矩阵 gx ,后者用于计算图像 y 方向像素梯度矩阵 gy。具体形式为:
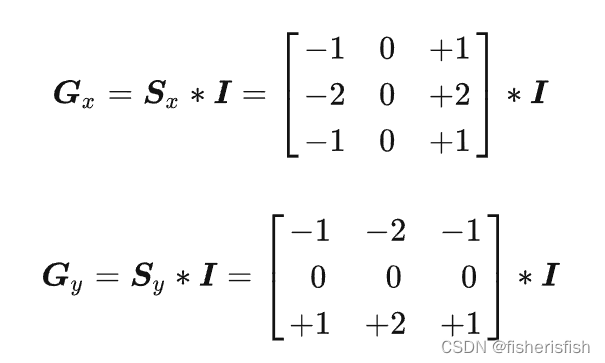
step3:非极大值像素梯度抑制,非极大值像素梯度抑制的目的在于消除边缘检测带来的杂散响应,起到将边缘“瘦身”的作用。其基本方法是将当前像素梯度强度与沿正负梯度方向上的相邻像素的梯度强度进行比较,若其最大(即为极值),则保留该像素为边缘点,若不是最大,则对其进行抑制,不将其作为边缘点。为了更精确计算,通常在跨越梯度方向的两个相邻像素之间使用线性插值来得到要参与比较的像素梯度。
step4:阈值滞后处理,定义一个高阈值和一个低阈值,即threshold1和threshold2。梯度强度低于低阈值的像素点被抑制,不作为边缘点;高于高阈值的像素点被定义为强边缘,保留为边缘点;处于高低阈值之间的定义为弱边缘,留待进一步处理。
step5:孤立弱边缘抑制,通常而言,由真实边缘引起的弱边缘像素点将连接到强边缘像素点,而噪声响应则未连接。通过查看弱边缘像素及其8个邻域像素,可根据其与强边缘的连接情况来进行判断。一般,可定义只要其中邻域像素其中一个为强边缘像素点,则该弱边缘就可以保留为强边缘,即真实边缘点。
对于应用来说,我们只要学会调节threshold1和threshold2来保存想要的边界即可,一般可以定义threshold1=2*threshold2。
由于待检测深度图像有黑边,所以用cv::rect(w,h,dw,dh)裁剪了一下,得到roi
cv::mat gray;
cvtcolor(res, gray, color_bgr2gray);
cv::mat out;
canny_dp(gray, out, 80, 50, 3, 1);
cv::rect cut_image = cv::rect(50, 0, dwidth - 100, dheight);
cv::mat roi = out(cut_image);然后从roi中取边缘点datapoint,并且为了实现dbscan设计了point数据类型
vector<point> datapoint;
// 将所有点集存储到temppoint
for (int i = 0; i < roi.rows; i++)
{
for (int j = 0; j < roi.cols; j++)
{
if (roi.at<uchar>(i, j) > 0) {
roi.at<uchar>(i, j) = 255;
point p(i, j);
datapoint.push_back(p);
}
}
}主要包括其在图像中的坐标x,y,点的类型pointtype,点所属的簇cluster这些均由dbscan算法给出,定义点的时候只要输入x,y坐标即可
class point {
public:
float x;
float y;
int pointtype;//1 noise 2 border 3 core
int visited;
int cluster;
int pts;
vector<point*> n; //point指针的向量
point() {}
point(float a, float b) :x(a), y(b) {
pointtype = 1;
visited = 0;
cluster = 0;
pts = 0;
}
};dbscan算法c++代码实现如下,具体输入为待聚类的点集dataset,聚类半径eps,聚类半径内点的最小数minpts,具体做法简单而言就是遍历点,然后在该点的eps内如果有大于minpts的点,则将该点记为核心点并聚类,最终的输出为聚类后的边缘点集,其属性为x,y,cluster。
//1 计算两点距离
float dis(point a, point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
//2 dbscan聚类函数
vector<point> dbscan(vector<point> dataset, float eps, int minpts)
{
int count = 0;
int len = dataset.size();
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
{
if (i == j)continue;
else if (dis(dataset[i], dataset[j]) < eps)
{
dataset[i].n.push_back(&dataset[j]);
}
}
}
for (int i = 0; i < len; i++)
{
if (dataset[i].visited == 1)continue;
dataset[i].visited = 1;
if (dataset[i].n.size() >= minpts)
{
count++;
dataset[i].pointtype = 3;
dataset[i].cluster = count;
for (int j = 0; j < dataset[i].n.size(); j++)
{
if (dataset[i].n[j]->visited == 1)continue;//访问dataset[j]的属性
dataset[i].n[j]->visited = 1; //dataset[i].n[j]-> 就是dataset[j]
if (dataset[i].n[j]->n.size() > minpts)
{
for (int k = 0; k < dataset[i].n[j]->n.size(); k++)
dataset[i].n.push_back(&(*(dataset[i].n[j]->n[k]))); //传递另一个dataset向量里面的元素内的成员n里面存储其他dataset的地址值,注意得到的是地址
dataset[i].n[j]->pointtype = 3;
}
else dataset[i].n[j]->pointtype = 2;
if (dataset[i].n[j]->cluster == 0)
dataset[i].n[j]->cluster = count;
}
}
}
//output
vector<point> clusterpoint;
for (int i = 0; i < len; i++) {
if (dataset[i].pointtype == 2) //边界点
clusterpoint.push_back(dataset[i]);
}
for (int i = 0; i < len; i++) {
if (dataset[i].pointtype == 3) //核心点
clusterpoint.push_back(dataset[i]);
}
return clusterpoint;
}
如果聚类出的点集不是无,那么进行下一步,首先获取聚类的簇数量和标签,然后再对每簇进行循环,取出簇中的点,并用rotatedrect box = minarearect(cv::mat(temppoint));函数计算最小包围框,并在res图像里画出这些框,flag是有缺陷的标志。
if (clusterpoint.size() != 0) {
flag = true;
int cluster = clusterpoint[0].cluster;
int clusternum = 1;
vector<int> label;
label.push_back(cluster);
for (int i = 0; i < clusterpoint.size(); i++)
{
if (clusterpoint[i].cluster != cluster) {
clusternum++;
cluster = clusterpoint[i].cluster;
label.push_back(cluster);
}
}
for (int j = 0; j < label.size(); j++) {
vector<point> temppoint;
for (int i = 0; i < clusterpoint.size(); i++) {
if (clusterpoint[i].cluster == label[j]) {
temppoint.push_back(cv::point(clusterpoint[i].y + 50, clusterpoint[i].x));
}
}
rotatedrect box = minarearect(cv::mat(temppoint));
point2f vertex[4];
box.points(vertex);
//绘制出最小面积的包围矩形
for (int i = 0; i < 4; i++)
{
line(res, vertex[i], vertex[(i + 1) % 4], scalar(100, 200, 211), 2, line_aa);
}
}
}




发表评论