NumPy 通用函数(ufunc)的实现_Python

numpy 中的通用函数（ufunc）是一类对数组元素进行逐元素操作的函数，它们能高效地处理数组的数学运算、统计聚合与数组操作等任务，返回结果也是数组。下面我们针对常用的 ufunc 进行分类说明。

1 数学运算类 ufunc

1.1 指数函数：np.exp()

计算数组中每个元素的自然指数（即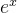，其中 ≈ 2.71828）。

代码示例：

import numpy as np
b = np.arange(3)  # 创建数组[0, 1, 2]
print("原始数组b:", b)
print("np.exp(b)的结果:", np.exp(b))  # 输出[1.         2.71828183 7.3890561]

1.2 平方根函数：np.sqrt()

计算数组中每个元素的平方根。

代码示例：

print("np.sqrt(b)的结果:", np.sqrt(b))  # 输出[0.         1.         1.41421356]

1.3 加法函数：np.add()

对两个数组执行逐元素加法运算。

代码示例：

c = np.array([2., -1., 4.])
print("原始数组c:", c)
print("np.add(b, c)的结果:", np.add(b, c))  # 输出[2.  0.  6.]

2 统计与聚合类 ufunc

这类函数用于对数组进行统计分析，如求极值、求和、求均值等。

2.1 最大值函数：np.max()

返回数组中的最大值，也可通过数组方法 arr.max() 调用。

代码示例：

arr = np.array([3, 1, 4, 1, 5])
print("数组最大值:", np.max(arr))  # 输出5

2.2 最小值函数：np.min()

返回数组中的最小值，也可通过数组方法 arr.min() 调用。

代码示例：

print("数组最小值:", np.min(arr))  # 输出1

2.3 求和函数：np.sum()

计算数组所有元素的和，也可通过数组方法 arr.sum() 调用。

代码示例：

print("数组元素和:", np.sum(arr))  # 输出3+1+4+1+5=14

2.4 均值函数：np.mean()

计算数组元素的算术平均值，也可通过数组方法 arr.mean() 调用。

代码示例：

print("数组均值:", np.mean(arr))  # 输出14/5=2.8

3 数组操作类 ufunc

这类函数用于对数组结构或元素顺序进行操作。

3.1 排序函数：np.sort()

对数组元素进行排序（返回新数组，原数组不变）。

代码示例：

arr = np.array([5, 2, 9, 1, 7])
sorted_arr = np.sort(arr)
print("排序后数组:", sorted_arr)  # 输出[1 2 5 7 9]

3.2 索引排序函数：np.argsort()

返回数组元素排序后的索引位置（即原数组中元素从小到大的位置编号）。

【数组的索引】

在 numpy 中，“索引” 是访问、修改或筛选数组元素的关键方式，其功能丰富且灵活。和 python 列表类似，一维数组的索引从 0 开始，可通过整数索引获取单个元素，也能用切片（如arr[1:4]）获取连续区间的元素；对于多维数组，需用逗号分隔的索引元组来指定维度，比如二维数组 arr 可通过 arr[行索引, 列索引] 精准定位元素，也能对某一维度单独切片（如 arr[:, 2] 获取所有行的第三列）。此外，布尔索引更是便捷，通过构造与原数组形状相同的布尔数组（如arr > 10），可直接筛选出满足条件的元素，这在数据清洗和分析中极为实用。简言之，索引机制让 numpy 数组的元素操作既高效又灵活，是掌握 numpy 数据处理能力的核心基础之一。

代码示例：

indices = np.argsort(arr)
print("排序索引:", indices)  # 输出[3 1 0 4 2]，表示原数组第3个元素（1）最小，第1个元素（2）次之……

3.3 非零元素查找：np.nonzero()

返回数组中非零元素的索引。

代码示例：

arr = np.array([0, 2, 0, 5, 0])
nonzero_indices = np.nonzero(arr)
print("非零元素索引:", nonzero_indices)  # 输出(array([1, 3]),)，表示第1、3个元素非零

代码示例中，(array([1, 3]),) 是 numpy 中 np.nonzero() 函数返回的结果格式，本质是一个包含 1 个 numpy 数组的元组。

其中，元组内的 array([1, 3]) 表示 “非零元素在数组中的索引位置”—— 比如当对一维数组 [0, 2, 0, 5, 0] 使用 np.nonzero() 时，数组中值不为 0 的元素（2 和 5）分别位于第 1 位和第 3 位（numpy 索引从 0 开始），因此返回该索引数组；而外层的元组结构是为了适配多维数组场景：若处理的是二维数组，np.nonzero() 会返回包含两个数组的元组（分别对应非零元素的 “行索引” 和 “列索引”），即使是一维数组，也保持元组格式以保证接口一致性，末尾的逗号则是 python 中单个元素元组的标准写法（避免与普通括号混淆）。

然而，这里的难点在于对于多维数组的情况。

代码示例：

# 创建一个形状为(2, 3, 2)的三维数组
arr_3d = np.array([
    [[0, 1], [2, 0], [0, 3]],
    [[4, 0], [0, 5], [6, 0]]
])
nonzero_indices = np.nonzero(arr_3d)
print("非零元素的三维索引:", nonzero_indices)

上述代码运行后会输出：

非零元素的三维索引: (array([0, 0, 0, 1, 1, 1]), array([0, 1, 2, 0, 1, 2]), array([1, 0, 1, 0, 1, 0])) 。

我们可以对 arr_3d，逐个找出非零元素的位置，就能明白这个结果是怎么来的了。

arr_3d 的形状是 (2, 3, 2)，可以理解为 “2 个深度层，每个深度层有 3 行、2 列”，具体结构如下：

# 深度0的层（arr_3d[0]）：
[
  [0, 1],  # 行0：列0是0，列1是1（非零）
  [2, 0],  # 行1：列0是2（非零），列1是0
  [0, 3]   # 行2：列0是0，列1是3（非零）
]

# 深度1的层（arr_3d[1]）：
[
  [4, 0],  # 行0：列0是4（非零），列1是0
  [0, 5],  # 行1：列0是0，列1是5（非零）
  [6, 0]   # 行2：列0是6（非零），列1是0
]

接下来，我们逐个找出所有非零元素，并记录它们的 “三维坐标”（深度索引，行索引，列索引）：

深度 0、行 0、列 1 的元素是 1（非零）→ 坐标 (0, 0, 1)
深度 0、行 1、列 0 的元素是 2（非零）→ 坐标 (0, 1, 0)
深度 0、行 2、列 1 的元素是 3（非零）→ 坐标 (0, 2, 1)
深度 1、行 0、列 0 的元素是 4（非零）→ 坐标 (1, 0, 0)
深度 1、行 1、列 1 的元素是 5（非零）→ 坐标 (1, 1, 1)
深度 1、行 2、列 0 的元素是 6（非零）→ 坐标 (1, 2, 0)

现在，把这 6 个坐标按顺序拆分：

所有坐标的 “深度索引” 提取出来：0, 0, 0, 1, 1, 1 → 组成第一个数组 array([0, 0, 0, 1, 1, 1])
所有坐标的 “行索引” 提取出来：0, 1, 2, 0, 1, 2 → 组成第二个数组 array([0, 1, 2, 0, 1, 2])
所有坐标的 “列索引” 提取出来：1, 0, 1, 0, 1, 0 → 组成第三个数组 array([1, 0, 1, 0, 1, 0])

这三个数组组合起来，就是 np.nonzero(arr_3d) 的返回结果，每个位置上的三个值对应一个非零元素的完整坐标。比如第 0 个位置的三个值 (0,0,1)，就对应第一个非零元素 arr_3d[0,0,1] = 1。