一、方法:多项式的numpy表示法
在数学中,多项式通常表示为(p(x) = 2x^3 + 3x^2 - 5x + 1),在numpy中,多项式被抽象为系数数组,但根据具体使用的工具不同,系数数组的排列顺序存在差异,这是初学者容易混淆的关键点。
1.1 两种核心表示方式对比
工具模块 | 系数排列顺序 | 示例(多项式\(3x^2 + 2x + 5\)) | 特点 |
|---|---|---|---|
| 升幂排列(索引对应幂次) |
| 功能全面,支持正交多项式,适合复杂计算 |
| 降幂排列(与数学书写一致) |
| 语法直观,操作简便,适合快速运算 |
在实际使用中,需根据场景选择合适的表示方式。若需进行高阶多项式计算或使用正交多项式,优先选择numpy.polynomial;若仅需简单的多项式运算与求值,numpy.poly1d会更便捷。
二、操作:numpy多项式核心操作详解
numpy多项式计算的核心操作包括创建多项式、求值、算术运算、求导与积分等。下面通过具体代码示例,逐一讲解这些操作的实现方法。
2.1 多项式的创建
import numpy.polynomial.polynomial as poly
# 创建多项式 3x² + 2x + 5
p = poly.polynomial([5, 2, 3])
print("创建的多项式:", p) # 输出:5.0 + 2.0 x + 3.0 x²
多项式求值是指计算多项式在指定自变量x处的函数值,numpy提供了两种常用方法:直接调用多项式对象,或使用polyval函数。
import numpy as np
# 单个点求值:x=2
single_val = p(2)
print("x=2时多项式的值:", single_val) # 结果:5 + 2*2 + 3*(2²) = 21
# 多个点求值:x=[1,2,3]
x_points = np.array([1, 2, 3])
multi_vals = p(x_points)
print("x=[1,2,3]时多项式的值:", multi_vals) # 输出:[10. 21. 38.]
# 直接使用polyval函数(系数数组+点)
coeffs = [5, 2, 3]
val_by_polyval = poly.polyval(2, coeffs)
print("polyval函数计算x=2的值:", val_by_polyval) # 输出:21
多项式对象直接求值:代码中p为通过numpy.polynomial.polynomial创建的多项式对象(系数数组[5,2,3])。直接调用p(2)和p(x_points),可分别实现单个点(x=2)和多个点(x=[1,2,3])的求值,结果与多项式理论计算一致(如x=2时,\(3*2^2 + 2*2 + 5 = 21\))。
polyval函数求值:通过poly.polyval(2, coeffs)直接对系数数组操作,无需创建多项式对象。其中第一个参数为求值点,第二个参数为多项式系数数组(需与numpy.polynomial的升幂排列规则一致),结果与对象调用方式相同。
2.2 多项式算术运算
numpy支持使用标准算术运算符(+、-、*、//、%)对多项式进行加减乘除运算,运算结果会自动合并同类项,无需手动处理。
# 定义两个简单多项式
p1 = poly.polynomial([1, 2]) # 1 + 2x
p2 = poly.polynomial([3, 4]) # 3 + 4x
# 加法:(1+2x) + (3+4x) = 4 + 6x
p_add = p1 + p2
print("多项式加法结果:", p_add) # 输出:4.0 + 6.0 x
# 减法:(1+2x) - (3+4x) = -2 - 2x
p_sub = p1 - p2
print("多项式减法结果:", p_sub) # 输出:-2.0 - 2.0 x
# 乘法:(1+2x)(3+4x) = 3 + 10x + 8x²
p_mul = p1 * p2
print("多项式乘法结果:", p_mul) # 输出:3.0 + 10.0 x + 8.0 x²
# 除法:返回商和余数(类似多项式长除法)
p_div, p_remainder = p_mul // p1, p_mul % p1
print("除法商:", p_div, ",余数:", p_remainder) # 输出:3.0 + 4.0 x ,余数:0.0
2.3 求根运算
多项式的根是使多项式值为 0 的 x 值,通过 roots 属性获取:

反过来,也可以通过根创建多项式(使用 np.poly()):

2.4 多项式的求导与积分
多项式的求导与积分是微积分中的基本操作,numpy分别通过deriv()和integ()方法实现,支持指定求导/积分的阶数。
# 定义多项式 5 + 2x + 3x²
p = poly.polynomial([5, 2, 3])
# 求导:d/dx (5 + 2x + 3x²) = 2 + 6x
p_deriv = p.deriv()
print("多项式的一阶导数:", p_deriv) # 输出:2.0 + 6.0 x
# 二阶导数
p_deriv2 = p.deriv(n=2)
print("多项式的二阶导数:", p_deriv2) # 输出:6.0
# 积分:∫(5 + 2x + 3x²)dx = 5x + x² + x³ + c(c为积分常数,默认0)
p_integ = p.integ()
print("多项式的积分(c=0):", p_integ) # 输出:0.0 + 5.0 x + 1.0 x² + 1.0 x³
# 指定积分常数c=2
p_integ_c = p.integ(k=2)
print("多项式的积分(c=2):", p_integ_c) # 输出:2.0 + 5.0 x + 1.0 x² + 1.0 x³
三、应用:多项式拟合与数据预测
多项式拟合是numpy多项式计算的重要应用场景,通过polyfit函数可以根据给定的数据点,拟合出最符合数据分布规律的多项式曲线,进而用于数据预测。
3.1 应用场景说明
假设我们有一组实验数据(x为自变量,y为因变量),数据中存在少量噪声。我们需要通过多项式拟合找到x与y之间的函数关系,并预测x=6时的y值。
3.2 代码实现与结果分析
import numpy as np
import matplotlib.pyplot as plt
# 1. 生成样本数据(模拟实验数据,加入少量噪声)
x = np.array([1, 2, 3, 4, 5])
y_true = x**2 + 1 # 真实关系:y = x² + 1
y = y_true + np.random.normal(0, 0.5, size=len(x)) # 加入噪声
# 2. 多项式拟合(拟合2次多项式)
deg = 2 # 多项式次数
coeffs = np.polyfit(x, y, deg=deg) # 返回降幂排列的系数
print("拟合得到的多项式系数(降幂):", coeffs) # 接近 [1, 0, 1]
# 3. 创建拟合多项式(使用poly1d,更直观)
p_fit = np.poly1d(coeffs)
print("拟合的多项式:", p_fit) # 输出类似:2
# 1 x + 0.1 x + 0.9(具体值因噪声略有差异)
# 4. 预测x=6时的值
x_pred = 6
y_pred = p_fit(x_pred)
print("x=6时的预测值:", y_pred) # 接近 6² + 1 = 37
# 5. 可视化拟合结果
x_plot = np.linspace(0.5, 6.5, 100) # 生成密集的x点用于绘图
y_plot = p_fit(x_plot)
plt.scatter(x, y, label='实验数据', color='red')
plt.plot(x_plot, y_plot, label=f'{deg}次多项式拟合', color='blue')
plt.plot(x_plot, x_plot**2 + 1, label='真实关系', color='green', linestyle='--')
plt.scatter(x_pred, y_pred, label=f'预测点({x_pred}, {y_pred:.2f})', color='orange', s=100)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('多项式拟合与数据预测示例')
plt.show()
结果
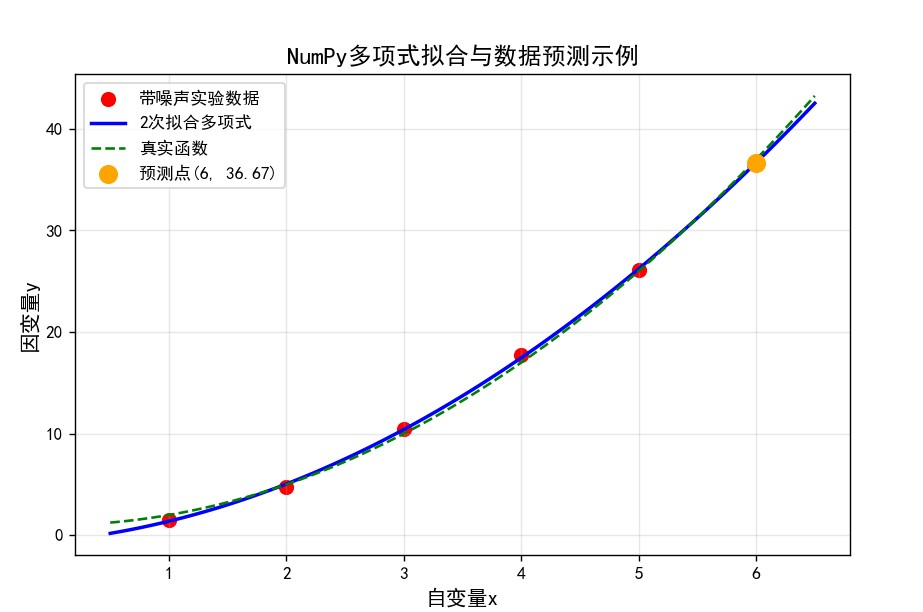
从拟合结果可以看出,即使数据中存在噪声,二次多项式仍能较好地逼近真实函数关系。通过拟合得到的多项式模型,我们成功预测了未知点的函数值。
- 红色散点(带噪声实验数据):对应代码中加了高斯噪声的实测值,是拟合的 “原始素材”。这些点围绕真实值小幅波动,模拟了现实中实验数据受干扰的情况。
- 绿色虚线(真实函数):代表理论关系 y = x^2 + 1,是隐藏在噪声下的 “真实规律”,作为判断拟合效果的基准。
- 蓝色实线(2 次拟合多项式):是通过
np.polyfit得到的拟合模型,几乎贴合所有红色散点,说明模型成功捕捉了数据的二次函数趋势,消除了噪声干扰。 - 橙色大点(预测点):对应 (x=6) 时的预测值,落在蓝色拟合曲线上,且接近绿色虚线的理论值(37),直观体现了拟合模型对 “未知数据” 的预测能力。
整体来看,这张图清晰验证了:二次多项式拟合能有效还原带噪声数据的真实规律,且可用于可靠的数值预测。
四、其他:注意事项
4.1 系数排列顺序的易错点
务必区分numpy.polynomial(升幂)与numpy.poly1d(降幂)的系数排列顺序,避免因混淆导致计算错误。建议在代码中添加注释,明确系数数组对应的多项式形式。
4.2 高阶多项式的数值稳定性
当多项式次数较高(如超过10次)时,普通幂基多项式可能出现数值不稳定问题(如龙格现象)。此时可改用numpy提供的正交多项式类,如切比雪夫多项式(chebyshev)、勒让德多项式(legendre)等,它们在高阶计算中具有更好的数值稳定性。
4.3 多项式根的求解
求解多项式方程x^2-5x+6的根,可使用poly1d类的roots属性或polyroots函数,示例如下:
p_roots = np.poly1d([1, -5, 6]) # 多项式x² -5x +6
roots = p_roots.roots
print("多项式的根:", roots) # 输出:[3. 2.],即x=2和x=3是方程的解
4.4 影响效率的关键因素
主要受多项式次数和输入数据规模影响:低次、小规模数据下,效率无明显瓶颈;高次(百次级)+大规模(千万级样本)场景,需注意内存占用和计算耗时,可通过降低多项式次数、分块处理数据等方式优化。
numpy多项式计算在绝大多数科学计算和数据分析场景中(如曲线拟合、简单预测、工程建模),效率完全能满足需求,是平衡易用性和性能的优选方案。仅在极端高次、超大规模数据场景下,需结合具体需求进行针对性优化。
五、总结
numpy为多项式计算提供了丰富且高效的工具,从基础的创建、求值、运算,到进阶的拟合、预测,覆盖了多项式应用的主要场景。本文通过系统的讲解和实例演示,帮助读者掌握了numpy多项式计算的核心技能。在实际应用中,需根据具体需求选择合适的多项式表示方式与操作方法,同时注意数值稳定性等关键问题。
主要优势在于:
- 用系数数组直观表示多项式
- 支持各种数学运算(加减乘除、求导、积分等)
- 提供求根和数据拟合功能
- 语法简洁,与数学表达式高度一致
到此这篇关于numpy多项式计算的实现方法的文章就介绍到这了,更多相关numpy多项式计算内容请搜索代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持代码网!





发表评论