激活函数是神经网络中至关重要的组成部分,它们为网络引入了非线性特性,使得神经网络能够学习复杂模式。pytorch 提供了多种常用的激活函数实现。
常用激活函数
1. relu (rectified linear unit)
数学表达式:
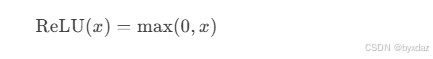
pytorch实现:
torch.nn.relu(inplace=false)
特点:
- 计算简单高效
- 解决梯度消失问题(正区间)
- 可能导致"神经元死亡"(负区间梯度为0),relu 在输入为负时输出恒为 0,导致反向传播中梯度消失,相关权重无法更新14。若神经元长期处于负输入状态,则会永久“死亡”,失去学习能力。
示例:
relu = nn.relu() input = torch.tensor([-1.0, 0.0, 1.0, 2.0]) output = relu(input) # tensor([0., 0., 1., 2.])
2. leakyrelu
数学表达式:
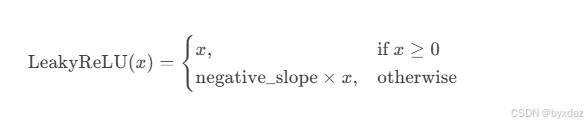
pytorch实现:
torch.nn.leakyrelu(negative_slope=0.01, inplace=false)
特点:
- 解决了relu的"神经元死亡"问题,通过引入负区间的微小斜率(如 torch.nn.leakyrelu(negative_slope=0.01)),保留负输入的梯度传播,避免神经元死亡。
- negative_slope通常设为0.01
示例
leaky_relu = nn.leakyrelu(negative_slope=0.1) input = torch.tensor([-1.0, 0.0, 1.0, 2.0]) output = leaky_relu(input) # tensor([-0.1000, 0.0000, 1.0000, 2.0000])
3. sigmoid
数学表达式:

pytorch实现:
torch.nn.sigmoid()
特点:
- 输出范围(0,1),适合二分类问题
- 容易出现梯度消失问题
- 输出不以0为中心
示例:
sigmoid = nn.sigmoid() input = torch.tensor([-1.0, 0.0, 1.0, 2.0]) output = sigmoid(input) # tensor([0.2689, 0.5000, 0.7311, 0.8808])
4. tanh (hyperbolic tangent)
数学表达式:
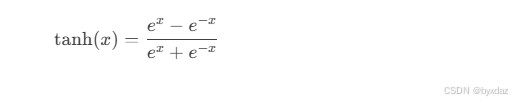
pytorch实现:
torch.nn.tanh()
特点:
- 输出范围(-1,1),以0为中心
- 比sigmoid梯度更强
- 仍存在梯度消失问题
示例:
tanh = nn.tanh() input = torch.tensor([-1.0, 0.0, 1.0, 2.0]) output = tanh(input) # tensor([-0.7616, 0.0000, 0.7616, 0.9640])
5. softmax
数学表达式:
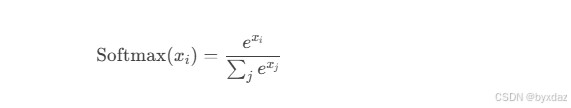
pytorch实现:
torch.nn.softmax(dim=none)
特点:
- 输出为概率分布(和为1)
- 常用于多分类问题的输出层
- dim参数指定计算维度
示例:
softmax = nn.softmax(dim=1) input = torch.tensor([[1.0, 2.0, 3.0]]) output = softmax(input) # tensor([[0.0900, 0.2447, 0.6652]])
其他激活函数
6. elu (exponential linear unit)
torch.nn.elu(alpha=1.0, inplace=false)
7. gelu (gaussian error linear unit)
torch.nn.gelu()
8. swish
class swish(nn.module):
def forward(self, x):
return x * torch.sigmoid(x)选择指南
- 隐藏层:通常首选relu及其变体(leakyrelu、elu等)
- 二分类输出层:sigmoid
- 多分类输出层:softmax
- 需要负输出的情况:tanh或leakyrelu
- transformer模型:常用gelu
自定义激活函数
pytorch可以轻松实现自定义激活函数:
class customactivation(nn.module):
def __init__(self):
super().__init__()
def forward(self, x):
return torch.where(x > 0, x, torch.exp(x) - 1)注意事项
- 梯度消失/爆炸问题
- 死亡神经元问题(特别是relu)
- 计算效率考虑
- 初始化方法应与激活函数匹配





发表评论